Benutzer:Buss-Haskert/Terme/Terme mit Klammern: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 24: | Zeile 24: | ||
aus + wird - <br> | aus + wird - <br> | ||
aus - wird + <br> | aus - wird + <br> | ||
Merke dir als Bild den Blitz [[Datei:Flash-1015467 1920.jpg|rahmenlos| | Merke dir als Bild den Blitz [[Datei:Flash-1015467 1920.jpg|rahmenlos|50px]], denn wenn du diese Klammer auflöst, musst du aufpassen!|Arbeitsmethode}} | ||
Beispiele: <br> | Beispiele: <br> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
5a <span style="color:red">'''-'''</span> (6b + 7a) |[[Datei:Flash-1015467 1920.jpg|rahmenlos| | 5a <span style="color:red">'''-'''</span> (6b + 7a) |[[Datei:Flash-1015467 1920.jpg|rahmenlos|50px]] Klammer auflösen (Zeichen umkehren)<br> | ||
= 5a - 6b - 7a |gleichartige Terme zusammenfassen<br> | = 5a - 6b - 7a |gleichartige Terme zusammenfassen<br> | ||
= -2a - 6b <br> | = -2a - 6b <br> | ||
</div> | </div> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
8x <span style="color:red">'''-'''</span> (-9y - 4x) |[[Datei:Flash-1015467 1920.jpg|rahmenlos| | 8x <span style="color:red">'''-'''</span> (-9y - 4x) |[[Datei:Flash-1015467 1920.jpg|rahmenlos|50px]] Klammer auflösen (Zeichen umkehren)<br> | ||
= 8x + 9y + 4x |gleichartige Terme zusammenfassen<br> | = 8x + 9y + 4x |gleichartige Terme zusammenfassen<br> | ||
= 12x + 9y | = 12x + 9y | ||
Version vom 2. März 2021, 20:11 Uhr
3) Terme mit Klammern
Einstieg noch ergänzen!
3.1 Pluszeichen vor der Klammer
Beispiele:
2a + (3b + 4a) |🌝 Klammer auflösen (weglassen)
= 2a + 3b + 4a |gleichartige Terme zusammenfassen
= 6a + 3b
-4x + (2y - 6x) |🌝 Klammer auflösen (weglassen)
= -4x + 2y - 6x |gleichartige Terme zusammenfassen
= -10x + 2y
3.2 Minuszeichen vor der Klammer
Beispiele:
3.3 Malzeichen vor der Klammer (Ausmultiplizieren)
KOPIE AUS DEM LERNPFAD Klasse 8...
Vergleiche deine Ideen mit denen im nachfolgenden Video:
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.
Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.

Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:
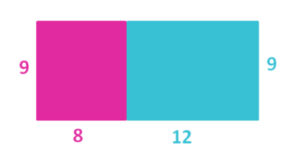
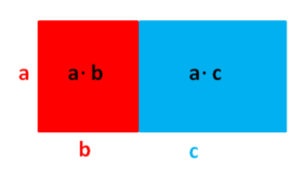
Auch hier ist das große Rechteck aus den kleinen Flächen zusammengesetzt. Der Flächeninhalt kann auf zwei Arten angegeben werden:
als Produkt der Seitenlängen a ⋅ ⟨b+c⟩ und als Summe der einzelnen Flächen a⋅b + a⋅c
Es gilt also: a⋅(b+c) = a⋅b + a⋅c.