Benutzer:Buss-Haskert/Terme/Terme vereinfachen

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU!!

Vorwissen zum Thema Terme
1) Variablen und Terme

2) Terme vereinfachen

2) Terme vereinfachen

EINSTIEGSAUFGABE NOCH ERGÄNZEN

2.1 Terme addieren und subtrahieren

Terme addieren und subtrahieren

Gleiche Variablen (gleichartige Terme) dürfen wir beim Addieren und Subtrahieren zusammenfassen.

Vorsicht: Unterschiedliche Variablen dürfen nicht addiert/subtrahiert werden!

Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft (Zeichnungen und Rechnungen):

  x+x+x = 3x



  x+y+x+y+x = x+x+x+y+y = 3x + 2y

Vorsicht: x, x² und x³ können NICHT zusammengefasst werden, denn sie sind nicht gleichartig!

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 1
• 2
• 3
• 4

Übung 2

Schreibe die Aufgabe aus dem Buch ab in dein Heft und vereinfache.

• S. 102 Nr. 1
• S. 102 Nr. 2
• S. 102 Nr. 3
• S. 102 Nr. 6

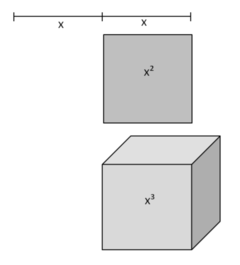
Bist du noch fit beim Addieren und Subtrahieren von negativen Zahlen?
-s + 3s = 2s Geschichte: Du hast 1€ Schulden und bekommst 3 Taschengeld. Dann hast du nun 2€ Guthaben.

Erfinde eine Geschichte zu Aufgabe f

Übung 3

Schreibe die Aufgabe aus dem Buch ab in dein Heft. Kreise gleichartige Terme mit derselben Farbe ein und vereinfache anschließend. (Das Einkreisen ist PFLICHT!)

• S. 102 Nr. 4
• S. 102 Nr. 5
• S. 102 Nr. 6
• S. 102 Nr. 7
• S. 102 Nr. 8

Zusätzliche Übungsmöglichkeiten findest du in den Learningapps:

2.2 Terme multiplizieren und dividieren

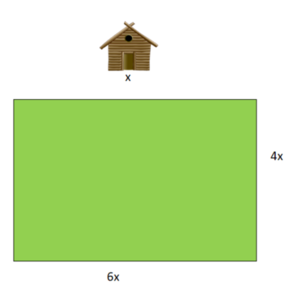
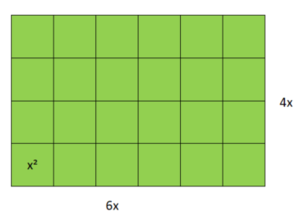
Die Giraffen im Zoo sollen ein neues Außengehege bekommen. Dies soll 6-mal so lang und 4-mal so breit werden wie das Giraffenhaus.
Welche Fläche steht den Giraffen dann außen zur Verfügung?

Erinnerung: Flächeninhalt eines Rechtecks:
A = a∙b

Flächeninhalt (Rechteck) = Länge ∙ Breite

Länge des Rechtecks: 6x
Breite des Rechtecks: 4x

A = 6x ∙ 4x

A = 6∙x ∙ 4∙x    |sortiere, vertausche die Reihenfolge der Faktoren
   = 6∙4∙x∙x    |fasse zusammen
   = 24x²

Zähle die kleinen Quadrate, du erhältst ebenfalls 24x².

Terme multiplizieren und dividieren

Wir dürfen beim Multiplizieren die Reihenfolge der Faktoren vertauschen. Danach multiplizieren wir die Zahlen und fassen wir gleiche Faktoren zu Potenzen zusammen.

Beim Dividieren dividieren durch eine Zahl dividiere nur die Zahlen.

Übertrage den Merksatz und die nachfolgenden Beispiele in dein Heft.
Beispiele:
a) a∙a = a²
b) 4b∙0,2b = 4∙0,2∙b∙b = 0,8b²
c) 12x∙7y = 12∙7∙x∙y = 84xy
d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d² e) 6ab:3b = $\tfrac{6\cdot a\cdot b}{3 \cdot b}$ = 2∙a (gekürzt)

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 4

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 5
• 6
• 8
• 10
• 11
• 12
• 13

Übung 5 (Multiplikation)

Schreibe die Aufgabe aus dem Buch ab in dein Heft und vereinfache.

• S. 104 Nr. 3
• S. 104 Nr. 4
• S. 104 Nr. 5
• S. 104 Nr. 8a
• S. 104 Nr. 10

Überlege "rückwärts": Welcher Term muss mit 7x multipliziert werden, damit das Produkt 28xy beträgt?
Zerlege 28xy in ein Produkt mit dem Faktor 7x:

28xy = 4∙7∙x∙y = 4y∙7x

Multipliziere die Zahlen und Variablen getrennt:
a) 2∙x∙4∙y   |Sortiere!
= 2∙4∙x∙y   |Berechne das Produkt der Zahlen!
= 8xy Lasse zum Schluss überflüssige Malpunkte weg.
f) t²∙5s∙t∙2s   |Sortiere!
= 5∙2∙s∙s∙t²∙t   |Berechne das Produkt der Zahlen und fasse die Variablen zu Potenzen zusammen! Erinnerung: t²∙t = t∙t∙t = t³

= 10s²t³ Sortiere die Variablen alphabetisch

{{Lösung versteckt|1=Multipliziere die Zahlen und Variablen getrennt:
c) 4x∙8xy∙5yb   |Sortiere!
= 4∙5∙8∙b∙x∙x∙y∙y   |Berechne das Produkt der Zahlen und fasse die Variablen zu Potenzen zusammen!
= 160bx²y² |2=Tipp zu Nr. 5|3=Verbergen}} {{Lösung versteckt|1=d) 25ab∙(-40bc)∙(-5c)  |Sortiere!
= 25∙(-5)∙(-40)∙a∙b∙b∙c∙c   |Berechne das Produkt der Zahlen (Tipp: verliebte Zahlen!) und fasse die Variablen zu Potenzen zusammen!
= -100∙(-40)∙ab²c²
= 4000ab²c²|2=Tipp zu Nr. 10d|3=Verbergen}}

Übung 6 (Division)

Schreibe die Aufgaben aus dem Buch ab in dein Heft und vereinfache.

• S. 104 Nr. 7
• S. 104 Nr. 8b

2.3 Vermischte Übungen

|Nun folgen Übungen, bei denen du entscheiden musst, ob Terme addiert/subtrahiert oder multipliziert/dividiert werden. Lies noch einmal die Merksätze auf dieser Seite. Sortiere in der nachfolgenden LearningApp passend.

Übung 7 - Vermischte Übungen

Nun folgen Übungen, bei denen du entscheiden musst, ob Terme addiert/subtrahiert oder multipliziert/dividiert werden. Lies noch einmal die Merksätze auf dieser Seite. Wende dann die richtige Regel an!

• S. 104 Nr. 6
• S. 104 Nr. 9
• S. 104 Nr. 11
• S. 104 Nr. 12(*) oder Nr. 13 (**)

Unterscheide zwischen den Rechenarten Strichrechung und Punktrechnung! Das Zusammenfassen der Terme ist unterschiedlich!
a) 5+5 = 10 aber 5∙5 = 25

c) a+a+a = 3a aber a∙a∙a = a³

a) a + 2a = 3a Das "hoch 2" bei a ist falsch, denn die Terme werden addiert, also dürfen gleichartige Terme zusammengefasst werden und die Terme a und 2a sind gleichartig, die Variable a bleibt unverändert.
x + x² kann nicht weiter zusammengefast werden, denn die Terme werde addiert, also dürfen nur gleichartige Terme zusammengefasst werden, x und x² sind nicht gleichartig.
c) vgl. b)
d) n²∙2n = 2n³ Die Terme werden multipliziert, daher werden die Zahlen und Variablen getrennt mutlipliziert und die Variablen werden zu Potenzen zusammengefasst, also
n²∙2n = 2∙n²∙n = 2n³
e) 2z² + 2z² = 4z² Die Terme werden addiert, die Terme sind gleichartig und dürfen zusammengefasst werden. Dabei bleibt die Variable z² gleich.

f) vgl. e)

Die Terme werden jeweils addiert, also dürfen gleichartige Terme zusammengefasst werden. Die Terme sind gleichartig, sie heißen nun z.B. "cd" statt nur c.

a) cd + cd = 1cd + 1cd = 2cd (Die Terme haben als gleichartige Variable "cd")

{{Lösung versteckt|1=Die Terme werden jeweils addiert/subtrahiert, es dürfen also gleichartige Terme zusammengefasst werden.
a) 5ab + 3mn - ab + 2mn   |Die Terme mit ab sind gleichartig und die mit mn. Diese fasse zusammen.
= 5ab - ab + 3mn + 2mn
= 4ba + 5mn|2=Tipp zu Nr. 13|3=Verbergen}}

Übung 8

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 14
• 15