Benutzer:Buss-Haskert/Trigonometrie/Sinus,Kosinus,Tangens: Unterschied zwischen den Versionen
K (Einstiegsaufgabe ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 1: | Zeile 1: | ||
==1) Sinus, Kosinus, Tangens - Seitenverhältnisse in rechtwinkligen Dreiecken==<br> | ==1) Sinus, Kosinus, Tangens - Seitenverhältnisse in rechtwinkligen Dreiecken==<br> | ||
=== 1.1 Steigung einer Straße === | ===1.1 Steigung einer Straße=== | ||
[[Datei:Steigung 12%.png|rahmenlos]]<br> | [[Datei:Steigung 12%.png|rahmenlos]]<br> | ||
Es gibt mehrere Möglichkeiten, die Steigung einer Straße anzugeben:<br> | Es gibt mehrere Möglichkeiten, die Steigung einer Straße anzugeben:<br> | ||
| Zeile 15: | Zeile 15: | ||
[[Datei:100% Steigung.png|rahmenlos]]|Tipp|Verbergen}} | [[Datei:100% Steigung.png|rahmenlos]]|Tipp|Verbergen}} | ||
<br> | <br> | ||
2. Angabe mithilfe des Steigungsdreiecks und m | 2. Angabe mithilfe des Steigungsdreiecks und m<br> | ||
Die Steigung einer Geraden f(x) = mx + b gibt der Faktor m an. Dazu zeichnest du das Steigungsdreieck. | Die Steigung einer Geraden f(x) = mx + b gibt der Faktor m an. Dazu zeichnest du das Steigungsdreieck.<br> | ||
[[Datei:Steigungsdreieck 12%.png|rahmenlos]] <br> | [[Datei:Steigungsdreieck 12%.png|rahmenlos|600px]] <br> | ||
m = <math>\tfrac{12}{100}</math> = 0,12<br> | m = <math>\tfrac{12}{100}</math> = 0,12<br> | ||
3. Angabe mithilfe des Steigungswinkels <math>\alpha</math> | 3. Angabe mithilfe des Steigungswinkels <math>\alpha</math> | ||
[[Datei:Steigungswinkel.png|rahmenlos]] | [[Datei:Steigungswinkel.png|rahmenlos|600px]] | ||
Das nachfolgende Applet zeigt diese drei Möglichkeiten noch einmal. Verändere die Steigung mithilfe des Schiebereglers und beobachte, was passiert. | Das nachfolgende Applet zeigt diese drei Möglichkeiten noch einmal. Verändere die Steigung mithilfe des Schiebereglers und beobachte, was passiert. | ||
Version vom 5. Januar 2021, 20:41 Uhr
==1) Sinus, Kosinus, Tangens - Seitenverhältnisse in rechtwinkligen Dreiecken==
1.1 Steigung einer Straße
Es gibt mehrere Möglichkeiten, die Steigung einer Straße anzugeben:
1. Angabe in Prozent
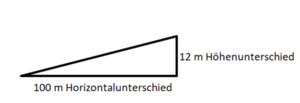
Das Verkehrsschild gibt die Steigung einer Straße in Prozent an.
a) Was bedeutet die Angabe von 12% Steigung? Erkläre!
Steigung =
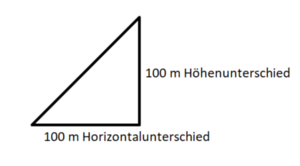
b) Gibt es eine Steigung, die größer als 100% ist?
Die Steigung 100% bedeutet 100m Höhenunterschied auf 100m Horizontalunterschied:
2. Angabe mithilfe des Steigungsdreiecks und m
Die Steigung einer Geraden f(x) = mx + b gibt der Faktor m an. Dazu zeichnest du das Steigungsdreieck.
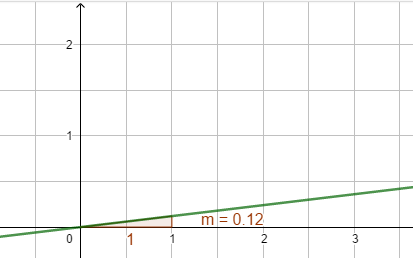
m = = 0,12
3. Angabe mithilfe des Steigungswinkels
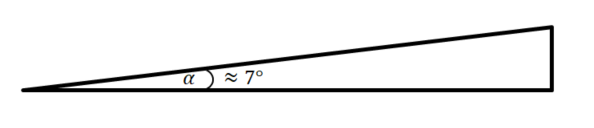
Das nachfolgende Applet zeigt diese drei Möglichkeiten noch einmal. Verändere die Steigung mithilfe des Schiebereglers und beobachte, was passiert.
Materialsammlung: Übungen auf der Seite Aufgabenfuchs
