Benutzer:ClaraS WWU-7/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 18: | Zeile 18: | ||
{{Lösung versteckt|1= Zeichne ein Baumdiagramm. Was sind die Ereignisse? | {{Lösung versteckt|1= Zeichne ein Baumdiagramm. Was sind die Ereignisse? | ||
|2=Tipp|3=Tipp}} | |2=Tipp|3=Tipp}} | ||
| Zeile 28: | Zeile 26: | ||
'''b)''' Für den Tafeldienst wird auch ein Zettel gezogen, jedoch hat die Lehrperson nun auch einen Zettel mit ihrem Namen hinzugefügt. Wie groß ist die Wahrscheinlichkeit, dass sie gezogen wird? | '''b)''' Für den Tafeldienst wird auch ein Zettel gezogen, jedoch hat die Lehrperson nun auch einen Zettel mit ihrem Namen hinzugefügt. Wie groß ist die Wahrscheinlichkeit, dass sie gezogen wird? | ||
{{Lösung versteckt|1= Wie viele Zettel sind nun in der Urne? {{ Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele | {{Lösung versteckt|1= Wie viele Zettel sind nun in der Urne? {{ Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}}|2=Tipps|3=Tipp}} | ||
{{Lösung versteckt|1= Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math>. | {{Lösung versteckt|1= Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math>. | ||
| Zeile 36: | Zeile 34: | ||
{{Box | Aufgabe 2: Schulfest|Bei eurem Schulfest gibt es eine Tombola. Bevor du blind ziehen darfst, wird dir einmal der Inhalt gezeigt, du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf | {{Box | Aufgabe 2: Schulfest|Bei eurem Schulfest gibt es eine Tombola. Bevor du blind ziehen darfst, wird dir einmal der Inhalt gezeigt, du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf die Bilder klicken, um sie in vergrößerter Form zu sehen. | ||
[[Datei:Urne A2 1.jpg|mini|Abbildung 1]][[Datei:Plakat.jpg|mini|Abbildung 2]] | [[Datei:Urne A2 1.jpg|mini|Abbildung 1]][[Datei:Plakat.jpg|mini|Abbildung 2]] | ||
| Zeile 70: | Zeile 68: | ||
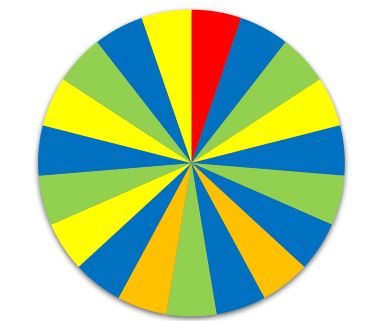
[[Datei:Glücksrad A3.jpg|zentriert]] | [[Datei:Glücksrad A3.jpg|zentriert]] | ||
{{Lösung versteckt| 1= Es gibt 1 rotes Feld, 2 orangene, 4 gelbe, 5 grüne und 7 blaue Felder. |2=Hilfe, falls du die Farben nicht unterscheiden kannst.|3=Hilfe, falls du die Farben nicht unterscheiden kannst.}} | |||
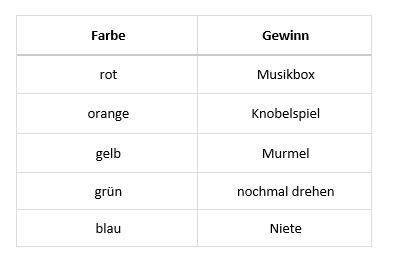
Man kann Folgendes gewinnen: | Man kann Folgendes gewinnen: | ||
[[Datei:Tabelle Glücksrad.jpg|zentriert]] | [[Datei:Tabelle Glücksrad.jpg|zentriert]] | ||
'''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also nochmal drehen. Beim zweiten Mal drehen landest du auf dem roten Feld. Wie groß ist die Wahrscheinlichkeit, dass diese beiden Fälle direkt hintereinander eintreten? | '''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also nochmal drehen. Beim zweiten Mal drehen landest du auf dem roten Feld. Wie groß ist die Wahrscheinlichkeit, dass diese beiden Fälle direkt hintereinander eintreten? | ||
{{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit nochmal drehen zu dürfen? Zeichne hierzu ein Baumdiagramm {{Lösung versteckt| 1= Nun kannst du das Baumdiagramm fortführen. Erinnerst du dich an die Pfadmultiplikationsregel? {{Box | Pfadmultiplikationsregel| Die | Merksatz}} | {{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit nochmal drehen zu dürfen? Zeichne hierzu ein Baumdiagramm {{Lösung versteckt| 1= Nun kannst du das Baumdiagramm fortführen. Erinnerst du dich an die Pfadmultiplikationsregel? {{Box | Pfadmultiplikationsregel| Bei der Pfadmultiplikationsregel werden die Wahrscheinlichkeiten der aufeinander folgenden Ereignisse mit einander multipilziert. | ||
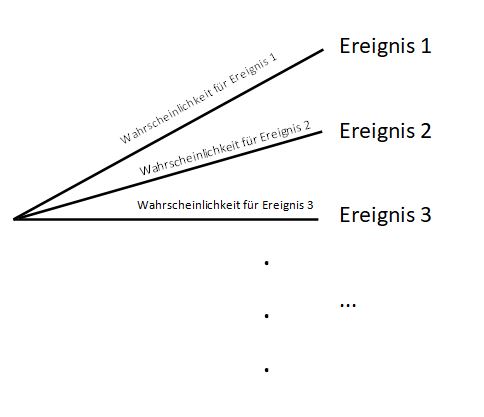
[[Datei:Pfadregel Multiplikation.jpg|links]] | |||
Die Wahrscheinlichkeit von (Ereignis A | Ereignis B) ist dann: | |||
<math>P(Ereignis A | Ereignis B)= Wahrscheinlichkeit A \cdot Wahrscheinlichkeit B </math> | |||
| Merksatz}} | |||
|2=Tipp|3= Tipp}}|2=Tipp|3=Tipp}} | |2=Tipp|3= Tipp}}|2=Tipp|3=Tipp}} | ||
Version vom 20. November 2020, 17:08 Uhr
Zufallsversuche
Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen.