Buss-Haskert/Quadratische Gleichungen

SEITE IM AUFBAU !!!

Lernpfad Quadratische Gleichungen

In diesem Lernpfad lernst du

• was quadratische Gleichungen sind,
• wie du quadratische Gleichungen lösen kannst,
• wie du Anwendungsaufgaben mithilfe von quadratischen Gleichungen löst.
  

Bearbeite die Schritte des Lernpfades selbständig. Stelle Fragen, wo du unsicher bist. Achte auf die Zeit!!

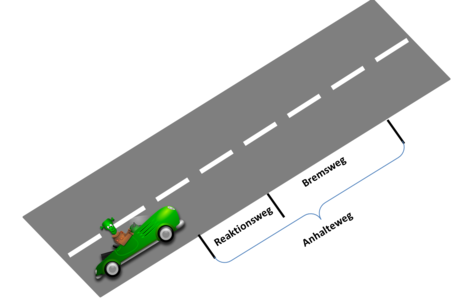
In der Fahrschule lernst du eine Faustformel für die Berechnung des Bremsweges:

Bremsweg in m:   s_B = ($\tfrac{v}{10}$)²

"s" bedeutet Weg bzw. Strecke; v steht für Geschwindigkeit (engl. velocity)

Hier handelt es sich um eine quadratische Gleichung, da die Variable v quadriert wird (v²).

Berechne den Bremsweg, wenn das Auto mit einer Geschwindigkeit von 30km/h fährt, also v=30 und wenn es mit einer Geschwindigkeit von 50km/h unterwegs ist.

Was fällt dir auf?
Vor Schulen oder Kindergärten sollten die Bremswege möglichst kurz sein. Wie schnell darf ein Auto fahren, damit der Bremsweg höchstens 4m beträgt?

Wenn v=30 beträgt, ist s_B = ($\tfrac{30}{10}$)² = 3² = 9 (m)
Für v=50 ist s_B = ($\tfrac{50}{10}$)² = 5² = 25(m)
Der Bremsweg ist also bei 50 km/h deutlich länger als bei 30 km/h, denn er hängt vom Quadrat der Geschwindigkeit ab.

Hier ist s=4m gegeben, die Gleichung muss also nach v aufgelöst werden. Dies lernst du in diesem Lernpfad!

Du siehst: Mathe ist überall! Du erarbeitest nun die Grundlagen zum Lösen solcher quadratischer Gleichungen.

1) Was sind quadratische Gleichungen?

Quadratische Gleichungen sind Gleichungen, in denen die Variable in zweiter Potenz (also z.B. x²) vorkommt.

Erinnerung: Lineare Gleichungen sind Gleichungen, in denen die Variable nur in erster Potenz (also z.B. x = x¹) vorkommt.

Entscheide in der nachfolgenden LearningApp, ob es sich um eine quadratische Gleichung handelt oder nicht.

2) Wie löse ich quadratische Gleichungen?

Quadratische Gleichungen kannst du zeichnerisch und rechnerisch lösen. Nutze für die zeichnerische Lösung GeoGebra und prüfe so immer deine rechnerischen Lösungen. Es gibt verschiedene Formen quadratischer Gleichungen. Die Lösungsstrategie hängt von der Form ab. Dies erklären die folgenden Kapitel.

2.1) Rein quadratische Gleichungen lösen

In der obigen Faustformel kommt die Variable v nur in quadratischer Form vor, also nur als v². Solche Gleichungen heißen "rein quadratisch". Sie haben immer die Form ax² = d (hier umgeformt $\tfrac{1}{100}$v² = s_B)

Rein quadratische Gleichungen

Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:

    ax² = d

Diese Gleichungen zu lösen hast du schon in der 9. Klasse gelernt. Wiederhole dein Wissen mithilfe der nachfolgenden Aufgaben.

Was ist die bei der letzten Aufgabe aufgefallen?

Bei der letzten Aufgabe muss im letzten Schritt $\sqrt{-2}$ berechnet werden. Dies ist nicht möglich, da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.

In den obigen Aufgaben erkennst du, dass eine rein quadratische Gleichung mehrere Lösungen haben kann:
zwei Lösungen, eine Lösung oder keine Lösung. Wovon hängt die Anzahl der Lösungen ab? Erkläre und begründe mithilfe der nachfolgenden Beispiele:

Zwei Lösungen:

1. x² = 169  |

...

Eine Lösung:

2. 2x² + 10 = 10  |

...

Keine Lösung:

3. -3x² = 108  |

...

Anzahl der Lösungen quadratischer Gleichungen

Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Die Gleichung hat zwei Lösungen, eine oder keine Lösung, wenn der Radikand positiv, null oder negativ ist.

Du kannst diese Gleichungen auch grafisch lösen:
Beispiel:
1. x² = 169 kannst du auch schreiben als x² - 169 = 0. Du berechnest also die Nullstellen der Funktion f(x) = x² - 169.

Wie hilft dir das nachfolgende Applet bei der Lösung der Gleichung 0,5x² = 4,5 ? Erkläre!

Nutze jeweils die GeoGebra-Applets, um deine gelösten Aufgaben zu kontrollieren.