Informatik am Johanneum/eigene Verfahren/17jojo: Unterschied zwischen den Versionen
17jojo (Diskussion | Beiträge) (kleine Fehlerbehebung) |
17jojo (Diskussion | Beiträge) (Sicherheitsbewertung eingefügt) |
||
| Zeile 386: | Zeile 386: | ||
===Sicherheitsbewertung=== | ===Sicherheitsbewertung=== | ||
Ein Nachteil meines Verfahrens ist, dass der Buchstabe „A“, im Gegensatz zu allen anderen Buchstaben, immer an der gleichen Stelle des Rechtecks liegt. Da der Buchstabe „A“ ein Vokal ist und im Deutschen häufig verwendet wird, kann man mit Hilfe einer Häufigkeitsanalyse weitere Buchstaben herausfinden. Dazu müsste man lediglich wissen, welche Buchstaben häufig auf den Buchstaben „A“ folgen. Mit diesen neuen Buchstaben könnte man im Anschluss daran weitere Buchstaben herausfinden. Eine Möglichkeit das Verfahren sicherer zu machen, wäre die Reihenfolge, in der die Buchstaben in das Rechteck sortiert werden, nicht vorzugeben. Denkbar wäre, dass der Empfänger des Schlüsselwortes anhand diesem auch erkennt, wie die Buchstaben im Rechteck anzuordnen sind. Damit würde man die Sicherheitslücke des „A´s“ umgehen. Des weiteren wäre es möglich, dass es keine festgelegten Buchstaben zur Bezeichnung der kleinen Rechtecke und Seiten gibt. An Stelle dessen könnten die Buchstaben nach einem anderen Prinzip ermittelt und verwendet werden. Positiv anzumerken ist, dass das Knacken des Geheimtextes ohne Kenntnis des Verschlüsselungsverfahrens eher schwierig ist. Dies liegt daran, dass die Buchstaben nicht einzeln verschlüsselt wurden, sondern in Zweiergruppen. Das manuelle Knacken würde wahrscheinlich sehr lange dauern, mit Hilfe eines Computers sollte es jedoch in kürzerer Zeit möglich sein, da es nur eine begrenzte Anzahl an Möglichkeiten gibt wie die Buchstaben im Rechteck angeordnet sein können. Abschließend ist festzuhalten, dass das Verfahren „ABYZ“ keine absolute Sicherheit versprechen kann. Im Bezug auf den Aufwand, der sowohl mit der Ver- als auch mit der Entschlüsselung verbunden ist, sollte man dementsprechend kritisch hinterfragen, ob es sich lohnt, den Text mit dem „ABYZ“- Verfahren zu verschlüsseln. | |||
Version vom 27. Mai 2020, 14:11 Uhr
ABYZ
Mein Verfahren ermöglicht die Verschlüsselung eines Textes, in dem Buchstabengruppen durch Zahlen und mathematische Zeichen ersetzt werden. Ausschlaggebend für die Verschlüsselung ist dafür die Position der einzelnen Buchstaben in einem Rechteck mit 6x5 Kästchen. Der Name „ABYZ“ leitet sich von den Namen vierer Rechtecke ab, die eine zentrale Rolle bei der Verschlüsselung spielen.
Verschlüsselung
Im Allgemeinen gibt es acht wesentliche Schritte, die bei Verschlüsselung einer Nachricht beachtet werden müssen.
1. Zu aller erst wählt man ein Schlüsselwort, welches man dem Empfänger übermittelt. Das Schlüsselwort kann jedes beliebige Wort sein. Einzig und allein die Anzahl der Buchstaben (x) ist im weiteren Vorgehen relevant.
2. Als nächstes sollte man die Buchstaben des ABCs notieren. Wichtig ist, dass man nach dem „Z“ noch die Buchstaben „Ä, Ö, Ü, ß“ in dieser Reihenfolge notiert.
3. Die Buchstaben bekommen jetzt von links nach rechts eine Ziffer zu geordnet. Dabei entspricht die niedrigste Ziffer der 1 und die höchste Ziffer x (der Anzahl der Buchstaben des Schlüsselwortes). Der erste Buchstabe (also das A) bekommt die Ziffer 1, der zweite Buchstabe (also das B) die Ziffer 2 und so weiter. Man zählt von links nach rechts immer x-Buchstaben ab und beginnt dann wieder von vorne.
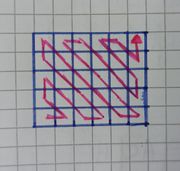
4. Nachdem jedem Buchstaben eine Ziffer zugeordnet wurde braucht man ein Rechteck mit 6x5 Kästchen. In jedes der Kästchen wird nun ein Buchstabe eingetragen. Der erste Buchstabe ist immer das A, da ihm zwangsläufig die Ziffer 1 zugeordnet wurde. Man beginnt unten links in der Ecke und trägt zuerst alle Buchstaben mit der Ziffer eins, dann mit der zwei und so weiter ein. Da es mehrere Buchstaben mit derselben Ziffer gibt beginnt man immer mit der ganz rechten, bzw. man arbeitet sich vom Anfang des Alphabetes zum Ende durch. (Auf dem Foto rechts kann man erkennen, in welcher Reihenfolge die Buchstaben in dem Rechteck einsortiert werden müssen.)
5. Das Rechteck wird nun in vier kleinere Rechtecke unterteilt. Das erste neue Rechteck heißt „A“. Es befindet sich links oben in der Ecke des Ausgangsrechtecks und hat die Maße von 3x2 Kästchen. Das zweite Rechteck befindet sich rechts oben, es heißt „B“, seine Größe beträgt 3x3 Kästchen. Das dritte Rechteck „y“ befindet sich links unten es ist 3x3 Kästchen groß. Das vierte und letzte Rechteck heißt „Z“ und befindet sich unten rechts. Seine Maße sind 3x2 Kästchen.
6. In jedem neuen Rechteck befinden sich nun entweder 6 oder 9 Buchstaben. Diesen Buchstaben wird als nächstes wieder eine Ziffer zugeordnet. Dabei erhält jeweils die Zahl oben links in einem Rechteck die Ziffer 1 und die Zahl unten rechts im Rechteck, je nachdem wie viele Buchstaben in dem Rechteck sind, die Ziffer 6 oder 9.
7. Wie in einigen anderen Verschlüsselungsverfahren müssen die einzelnen Wörter eurer Nachricht, die ihr Verschlüsseln wollt, immer eine gerade Anzahl an Buchstaben haben. Ist dies nicht der Fall, so wird der erste Buchstabe des Worts noch einmal am Ende des Wortes wiederholt.Folgt mehrfach der gleiche Buchstabe aufeinander, so werden diese Buchstaben jeweils durch ein „x“ getrennt.
Bevor die Nachricht verschlüsselt werden kann, muss sie Nachricht noch in Zweiergruppen unterteilt werden. Zwei aufeinanderfolgende Buchstaben bilden eine Gruppe.
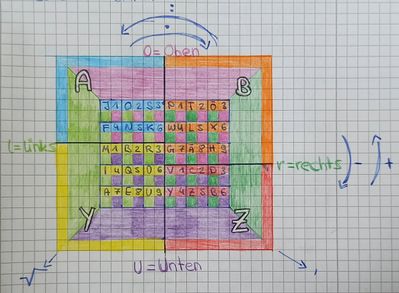
8. Die gebildeten Zweiergruppen geht man nun chronologisch durch und verschlüsselt sie. Ausschlaggebend ist dabei, in welchem der kleinen Rechtecke sich die Buchstaben befinden. Alle Buchstaben des Klartextes werden mit der Ziffer codiert, die ihr im Rechteck zugeordnet wurde. Zusätzlich werden noch einige Buchstaben und mathematische Symbole ergänzt, die Regeln dafür finden sich im Folgenden. (Auf dem Foto rechts ist eine grafische Zusammenfassung der im folgenden genannten Regeln abgebildet. Das Schlüsselwort lautet in diesem Beispiel "Haus".)
8.1 Beide Buchstaben befinden sich im selben Rechteck:
a) Sie befinden sich beide oben links („A“). Die Ziffer ersetzt werden durch ein „A“ getrennt, da dieses Rechteck „A“ heißt.
b) Sie befinden sich beide oben rechts („B“). Die Ziffern werden durch den Buchstaben „B“ getrennt.
c) Sie befinden sich beide unten links („Y“). Die Ziffern werden durch den Buchstaben „Y“ getrennt.
d) Sie befinden sich beide unten rechts („Z“). Die Ziffern werden durch den Buchstaben „Z“ getrennt.
8.2 Beide Buchstaben befinden sich in den linken Rechtecken („A“ und „Y“):
a) Der erste der beiden Buchstaben aus der zweier Gruppe befindet sich oben links („A“) und der zweite befindet sich unten links („Y“). Vor die Ziffern kommt der Buchstabe „L“ (für links) und sie werden durch ein „-“ getrennt.
b) Der erste der beiden Buchstaben befindet sich unten links („Y“) und der zweite oben links („A“). Vor die Ziffern kommt wieder das „L“ und sie werden durch ein „+“ getrennt.
8.3 Beide Buchstaben befinden sich in den rechten Rechtecken („B“ und „Z“):
a) Der erste der beiden Buchstaben aus der zweier Gruppe befindet sich oben rechts („B“) und der zweite befindet sich unten rechts („Z“). Vor die Ziffern kommt der Buchstabe „R“ (für rechts) und sie werden durch ein „-“ getrennt.
b) Der erste der beiden Buchstaben befindet sich unten rechts („Z“) und der zweite oben rechts („B“). Vor die Ziffern kommt wieder das „R“ und sie werden durch ein „+“ getrennt.
8.4 Beide Buchstaben befinden sich in den oberen Rechtecken („A“ und „B“):
a) Der erste der beiden Buchstaben aus der zweier Gruppe befindet sich oben links („A“) und der zweite oben rechts („B“). Vor die Ziffern kommt ein „O“ (für oben) und sie werden durch ein „*“ getrennt.
b) Der erste Buchstabe befindet sich oben rechts („B“) und der zweite oben links („A“). Vor die Ziffern kommt ein „O“ und die beiden werden durch ein „:“ getrennt.
8.5 Beide Buchstaben befinden sich in den unteren Rechtecken („Y“ und „Z“):
a) Der erste der beiden Buchstaben aus der zweier Gruppe befindet sich unten links („Y“) und der zweite unten rechts („Z“). Vor die Ziffern kommt ein „U“ (für unten) und sie werden durch ein „*“ getrennt.
b) Der erste Buchstabe befindet sich unten rechts („Z“) und der zweite unten links („Y“). Vor die Ziffern kommt ein „U“ und die beiden werden durch ein „:“ getrennt.
8.6 Die beiden Buchstaben sind in diagonal zueinanderstehenden Rechtecken:
a) Die Buchstaben befinden sich in den Rechtecken oben links („A“) und unten rechts („Z“): In diesem Fall ist es egal, in welchem der beiden Rechtecke sich welcher Buchstabe befindet. Die beiden Ziffern werden durch ein „,“ getrennt.
b) Die Buchstaben befinden sich in den Rechtecken oben rechts („B“) und unten links („Y“): In diesem Fall ist es egal, in welchem der beiden Rechtecke sich welcher Buchstabe befindet. Die beiden Ziffern werden durch „√“ getrennt.
Die Einzelnen Kombinationen aus Buchstaben, Ziffern und mathematischen Zeichen werden entsprechend der Buchstaben im Klartext aneinandergehängt.
Entschlüsselung
1. Zuerst benötigt man das gleiche Rechteck wie derjenige, der den Text verschlüsselt hat. Mithilfe des Codewortes ist es möglich sich dieses Rechteck zu erstellen. Die Anleitung dafür findet sich bei der Erklärung zur Verschlüsselung. (siehe oben)
2. Der Geheimtext muss dann in mehrere Gruppen unterteilt. Dies Bestehen aus maximal 4 und mindestens 3 Elementen (Buchstaben, Ziffern, mathematische Zeichen)
- Vierer Gruppen beginnen immer mit einem der folgenden vier Buchstaben: „O, U, L, R“
- Dreier Gruppen erkennt man daran, dass zwei Ziffern durch die folgenden Buchstaben oder mathematischen Zeichen getrennt sind: „A, B, Y, Z, , ,√“
3. Nun müssen die einzelnen Gruppen entschlüsselt werden.
3a) Einer der folgenden Buchstaben „A, B, Y, Z“ ist in der Gruppe enthalten:
Der Buchstabe gibt das Rechteck an, in welchem sich beide Ziffern befinden. In dem angegebenen Rechteck ersetzt man dann die Ziffern durch die Buchstaben, die ihnen zugeordnet sind.
3b) Buchstabe „O“ ist in der Gruppe enthalten: Beide Ziffern der Gruppe geben Buchstaben aus der oberen Rechtecken („A“ und „B“) an.
- Die Ziffern sind durch ein „:“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „B“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „A“
- Die Ziffern sind durch ein „*“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „A“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „B“
3c) Buchstabe „U“ ist in der Gruppe enthalten: Beide Ziffern der Gruppe geben einen Buchstaben aus den unteren Rechtecken („Y“ und “Z“) an.
- Die Ziffern sind durch ein „:“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „Z“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „Y“
- Die Ziffern sind durch ein „*“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „Y“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „Z“
3d) Buchstabe „L“ ist in der Gruppe enthalten: Beide Ziffern der Gruppe geben einen Buchstaben aus den linken Rechtecken („A“ und „y“) an
- Die Ziffern sind durch ein „+“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „y“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „A“
- Die Ziffern sind durch ein „-“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „A“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „y“
3e) Buchstabe „R“ ist in der Gruppe enthalten: Beide Ziffern der Gruppe geben einen Buchstaben aus den rechten Rechtecken („B“ und „Z“) an
- Die Ziffern sind durch ein „+“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „Z“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „B“
- Die Ziffern sind durch ein „-“ getrennt. Die Ziffer vor dem genannten Symbol codiert den Buchstaben aus dem Rechteck „B“, die zweite Ziffer codiert den Buchstaben aus dem Rechteck „Z“
3f) Es ist kein Buchstabe in der Gruppe enthalten.
- Ein „√“ ist enthalten. Die Ziffern codieren Buchstaben aus den Rechtecken „B“ und „y“. Welche Ziffer zu welchem Rechteck gehört muss durch ausprobieren herausgefunden werden.
- Ein „ , “ ist enthalten. Die Ziffern codieren Buchstaben aus den Rechtecken „A“ und „Z“. Welche Ziffer zu welchem Rechteck gehört muss durch ausprobieren herausgefunden werden.
4. Nachdem entschlüsseln müssen noch die zusätzlich hinzugefügten Buchstaben entfernt werden. Folgt der gleiche Buchstabe mehrfach aufeinander so wird er durch ein „x“ getrennt. Bei Wörtern, die eine ungerade Anzahl an Buchstaben haben wurde der Anfangsbuchstabe am Ende des Wortes noch einmal wiederholt.
Beispiel
Verschlüsselung
Der Satz EINVERSCHLUESSLUNGSVERFAHRENSOLLTEAUCHEINFACHANZUWENDENSEIN lässt sich mit meinem Verfahren folgendermaßen verschlüsseln:
1. Das gewählte Schlüsselwort lautet Haus. (= 4 Buchstaben)
2. Jedem Buchstaben wird eine Ziffer zugeteilt.
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Ä | Ö | Ü | ß |
3. Die Buchstaben werden in das 6x5 Kästchen Rechteck einsortiert.
| J | O | S | P | T | Ö |
| F | N | K | W | L | X |
| M | B | R | G | Ä | H |
| I | Q | Ü | V | C | D |
| A | E | U | Y | Z | B |
4. Das große Rechteck wird in vier kleinere Rechtecken unterteilt.
| J | O | S | P | T | Ö |
| F | N | K | W | L | X |
| M | B | R | G | Ä | H |
| I | Q | Ü | V | C | D |
| A | E | U | Y | Z | B |
Fett= Rechteck „A“
Kursiv= Rechteck „B“
Normal= Rechteck „y“
Unterstrichen= Rechteck „Z“
5. Die Buchstaben in den einzelnen Rechtecken werden durchnumeriert.
| J 1 | O2 | S3 | P1 | T2 | Ö3 |
| F4 | N5 | K6 | W4 | L5 | X6 |
| M1 | B2 | R3 | G7 | Ä8 | H9 |
| I4 | Q5 | Ü6 | V1 | C2 | D3 |
| A7 | E8 | U9 | Y4 | Z5 | B6 |
6. Der Klartext wird in Zweiergruppen unterteilen und neue Buchstaben werden einsetzten (falls nötig).
EI NE VE RS CH LÜ SX SE LU NG SV ER FA HR EN SO LX LT ES AU CH EI NF AC HE AN ZU WE ND EN SE IN
7. Die Buchstabengruppen werden mit Hilfe des bereits erklärten Schemas codiert.
EI= 8Y4 NE= L5-8 VE= U1:8 RS= L3+3 CH=R2+9 LÜ= 5√6 SX= O3*6 SE= L3-8 LU=5√9 NG=O5*7 SV=3,1 ER=8Y3 FA=L4-7 HR= 9√8 EN= L8+5 SO=3A2 LX=5B6 LT=5B2 ES= L8+3 AU=7Y9 CH=R2+9 EI=8Y4 NF=5A4 AC=U7*2 HE=9√8 AN=L5+7 ZU=U5:9 WE=O4:5 ND=5,3 EN=L8+5 SE= L3-8 IN=L4+5
8. Der fertige Geheimtext lautet:
8Y4L5-8 U1:8 L3+3R2+95√6 O3*6 L3-85√9O5*73,18Y3L4-7 9√8 L8+53A25B65B2 L8+37Y9R2+9 8Y45A4U7*29√8L5+7U5:9O4:55,3L8+5 L3-8L4+5
Entschlüsselung
1. Rechtecken mit Buchstaben und Ziffern Mithilfe des Schlüsselwortes „Haus“ erstellen. (Siehe Beispiel Verschlüsselung)
| J 1 | O2 | S3 | P1 | T2 | Ö3 |
| F4 | N5 | K6 | W4 | L5 | X6 |
| M1 | B2 | R3 | G7 | Ä8 | H9 |
| I4 | Q5 | Ü6 | V1 | C2 | D3 |
| A7 | E8 | U9 | Y4 | Z5 | B6 |
2. Geheimtext anhand der erklärten Kriterien (Siehe Entschlüsselung) in die unterschiedlichen Gruppen unterteilen.
8Y4 L5-8 U1:8 L3+3 R2+9 5√6 O3*6 L3-8 5√9 O5*7 3,1 8Y3 L4-7 9√8 L8+5 3A2 5B6 5B2 L8+3 7Y9 R2+9 8Y4 5A4 U7*2 9√8 L5+7 U5:9 O4:5 5,3 L8+5 L3-8 L4+5
3. Einzelne Gruppe nach den bereits erklärten Kriterien decodieren (siehe Entschlüsselung).
8Y4 = Das „y“ zeigt beiden Ziffern codieren Buchstaben im Rechteck „y“. Die Zahl 8 steht für E und die Zahl 4 für den Buchstaben I. 8Y4 ist entschlüsselt also EI.
L5-8= Das L zeigt beide Ziffern codieren Buchstaben der linken Rechtecke („A“ und „y“). Das „-“ zeigt, dass im Feld „A“ der Buchstabe die Ziffer 5 hat und der Buchstabe in Feld „Y“ hat die Ziffer 8. L5-8 ist entschlüsselt also NE.
…….
8Y4= EI L5-8=NE U1:8=VE L3+3=RS R2+9=CH 5√6=LÜ O3*6=SX L3-8=SE 5√9=LU O5*7=NG 3,1=SV 8Y3=ER L4-7=FA 9√8=HR L8+5=EN 3A2=SO 5B6=LX 5B2=LT L8+3=ES 7Y9=AU R2+9=CH 8Y4=EI 5A4=NF U7*2=AC 9√8=HE L5+7=AN U5:9=ZU O4:5=WE 5,3=ND L8+5=EN L3-8=SE L4+5=IN
4. Die entschlüsselte Nachricht lautet:
EI NE VE RS CH LÜ SX SE LU NG SV ER FA HR EN SO LX LT ES AU CH EI NF AC HE AN ZU WE ND EN SE IN
5. Der Fertige Klartext (ohne zusätzliche Buchstaben) lautet:
EIN VERSCHLÜSSELUNGSVERFAHREN SOLLTE AUCH EINFACH ANZUWENDEN SEIN.
Sicherheitsbewertung
Ein Nachteil meines Verfahrens ist, dass der Buchstabe „A“, im Gegensatz zu allen anderen Buchstaben, immer an der gleichen Stelle des Rechtecks liegt. Da der Buchstabe „A“ ein Vokal ist und im Deutschen häufig verwendet wird, kann man mit Hilfe einer Häufigkeitsanalyse weitere Buchstaben herausfinden. Dazu müsste man lediglich wissen, welche Buchstaben häufig auf den Buchstaben „A“ folgen. Mit diesen neuen Buchstaben könnte man im Anschluss daran weitere Buchstaben herausfinden. Eine Möglichkeit das Verfahren sicherer zu machen, wäre die Reihenfolge, in der die Buchstaben in das Rechteck sortiert werden, nicht vorzugeben. Denkbar wäre, dass der Empfänger des Schlüsselwortes anhand diesem auch erkennt, wie die Buchstaben im Rechteck anzuordnen sind. Damit würde man die Sicherheitslücke des „A´s“ umgehen. Des weiteren wäre es möglich, dass es keine festgelegten Buchstaben zur Bezeichnung der kleinen Rechtecke und Seiten gibt. An Stelle dessen könnten die Buchstaben nach einem anderen Prinzip ermittelt und verwendet werden. Positiv anzumerken ist, dass das Knacken des Geheimtextes ohne Kenntnis des Verschlüsselungsverfahrens eher schwierig ist. Dies liegt daran, dass die Buchstaben nicht einzeln verschlüsselt wurden, sondern in Zweiergruppen. Das manuelle Knacken würde wahrscheinlich sehr lange dauern, mit Hilfe eines Computers sollte es jedoch in kürzerer Zeit möglich sein, da es nur eine begrenzte Anzahl an Möglichkeiten gibt wie die Buchstaben im Rechteck angeordnet sein können. Abschließend ist festzuhalten, dass das Verfahren „ABYZ“ keine absolute Sicherheit versprechen kann. Im Bezug auf den Aufwand, der sowohl mit der Ver- als auch mit der Entschlüsselung verbunden ist, sollte man dementsprechend kritisch hinterfragen, ob es sich lohnt, den Text mit dem „ABYZ“- Verfahren zu verschlüsseln.