Herta-Lebenstein-Realschule/Ähnlichkeit und Strahlensätze/3) Strahlensätze: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Anwendungsaufgabe ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 112: | Zeile 112: | ||
===3.1) Die Strahlensätze anwenden=== | ===3.1) Die Strahlensätze anwenden=== | ||
Die Strahlensätze helfen, schwer zugängliche oder weit entfernte Streckenlängen zu bestimmen. | |||
{{Box|Strahlensätze anwenden|Gehe schrittweise vor: | |||
1. Was ist gegeben, was gesucht? Erstelle eine Strahlensatzfigur und trage die gegebenen Werte in die Skizze ein. | |||
Falls keine Strahlensatzfigur erkennbar ist, zeichne Hilfslinien ein. | |||
2. Stelle eine Verhältnisgleichung mithilfe der Strahlensätze auf. Tipp: Notiere die gesuchte Größe im Zähler, dann kannst du leichter rechnen. | |||
3. Löse die Gleichung. | |||
4. Notiere einen Antwortsatz mit Bezug zur gesuchten Größe.|Merksatz}} | |||
Beispiel: | |||
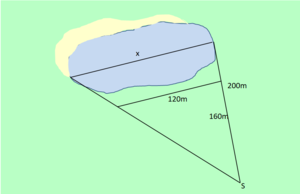
Die Länge eines Sees soll bestimmt werden. Dazu werden drei Strecken an Land gemessen und dann mit dem Strahlensatz die Länge des Sees berechnet. | |||
[[Datei:Anwendung 1 See.png|mini]] | |||
1. Die Strahlensatzfigur ist in der Skizze gegeben. Wo sind die Strahlen? Wo sind die Parallelen? | |||
2. Verhältnisgleichung: <math>\frac{x}{120}</math>=<math>\frac{200}{160}</math> | |||
3. Gleichung lösen: x = <math>\frac{200}{160}</math>·120 | |||
x = 150 | |||
4. Antwort: Der See ist 120m lang. | |||
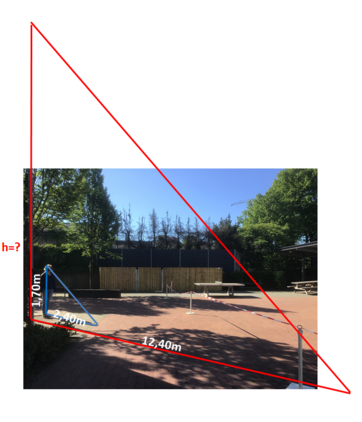
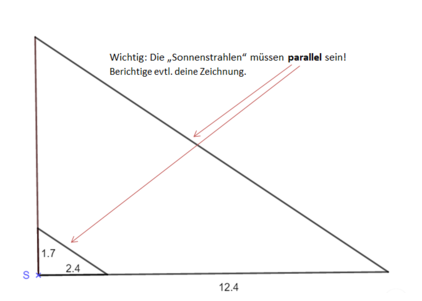
{{Box|Übung 1|Löse das Einstiegsproblem: Wie hoch ist der Baum auf dem Schulhof? Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums.|Üben}} | |||
Welche Größen mussten gemessen werden, um die Höhe des Baumes berechnen zu können? | |||
Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums. | Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums. | ||
[[Datei:Einsteigsbeispiel Baumhöhe Schule.png|422x422px]] | [[Datei:Einsteigsbeispiel Baumhöhe Schule.png|422x422px]] | ||
| Zeile 119: | Zeile 138: | ||
{{Lösung versteckt|1=Verhältnisgleichung: <math>\frac{x}{1,7}</math>=<math>\frac{12,4}{2,4}</math>|2=Hilfe: Verhältnisgleichung|3=Verbergen}} | {{Lösung versteckt|1=Verhältnisgleichung: <math>\frac{x}{1,7}</math>=<math>\frac{12,4}{2,4}</math>|2=Hilfe: Verhältnisgleichung|3=Verbergen}} | ||
{{Box|Übung 2|Löse auf der Seite Aufgabenfuchs die Anwendungsaufgaben Nr. 23 - 28. Zeichne jeweils die Strahlensatzfigur in dein HEft und löse schrittweise. Gib deine Lösung auf der Seite zur Kontrolle ein. | |||
[https://mathe.aufgabenfuchs.de/flaeche/dreieck/strahlensatz.shtml]|Üben}} | |||
<br /> | <br /> | ||
Version vom 10. Mai 2020, 05:56 Uhr
3) Strahlensätze
In der Umwelt lassen viele Strecken sich nicht messen, wie z.B. die Höhe von Bäumen oder die Breite eines Sees. Hier hilft die Mathematik!
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen):
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst.
Datei:Dreiecke Konstruktion Einstieg Strahlensätze 2.png
Für die Streckenverhältnisse ergeben sich immer gleiche Werte:
= 0,45
= 0,45
= = 0,6
= = 0,6
= 1,3
= 1,3
= Erinnerung: Das ist der Streckungsfaktor k
= = 2
= = 2
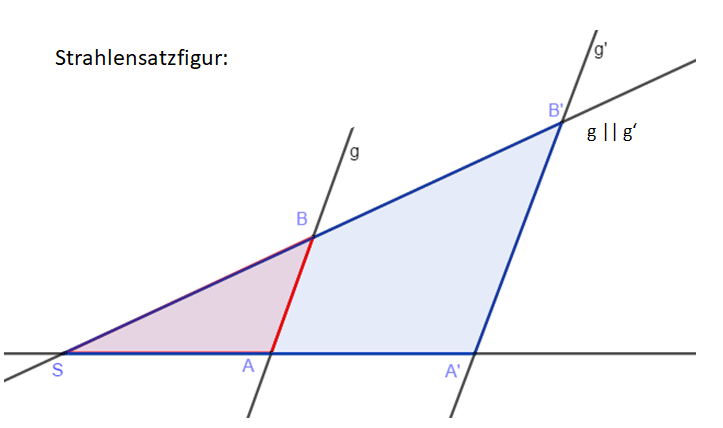
Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c = ; c' = usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die Strahlensätze.
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen.
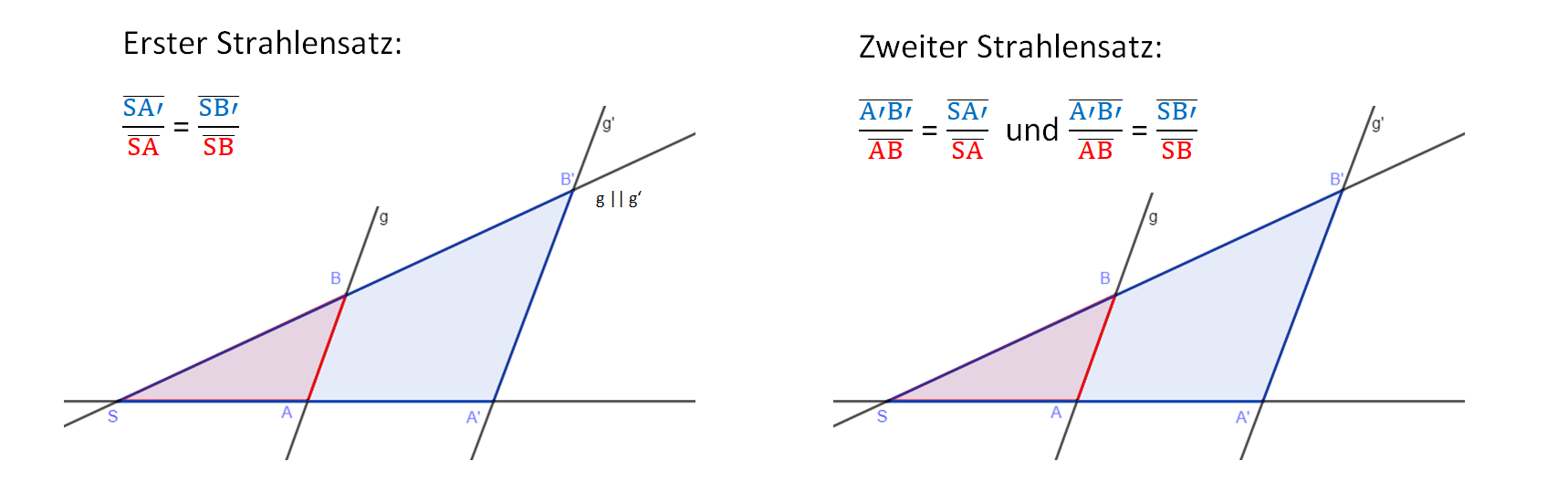
Die Streckenverhältnisse des ersten Strahlensatz heißen für unsere ähnlichen Dreiecke im Beispiel
==k
Die Streckenverhältnisse des zweiten Strahlensatzes sind in unserem Beispiel entsprechend
==k und ==kZum besseren Verständnis noch einmal links die Erklärung und rechts einige Beispiele in Videos:
Du kannst eine Ergebnisse mithilfe des GeoGebra-Applets prüfen. Stelle dazu die Längen mit den Schiebereglern passend ein.
Um die Strecke einzustellen, nutze den Schieberegler für die Strecke (oder bei Nr. 3 auch Schieberegler für die Strecke ) und verändere diese Länge so lange, bis der passende Wert für die Länge von erscheint.
Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse.


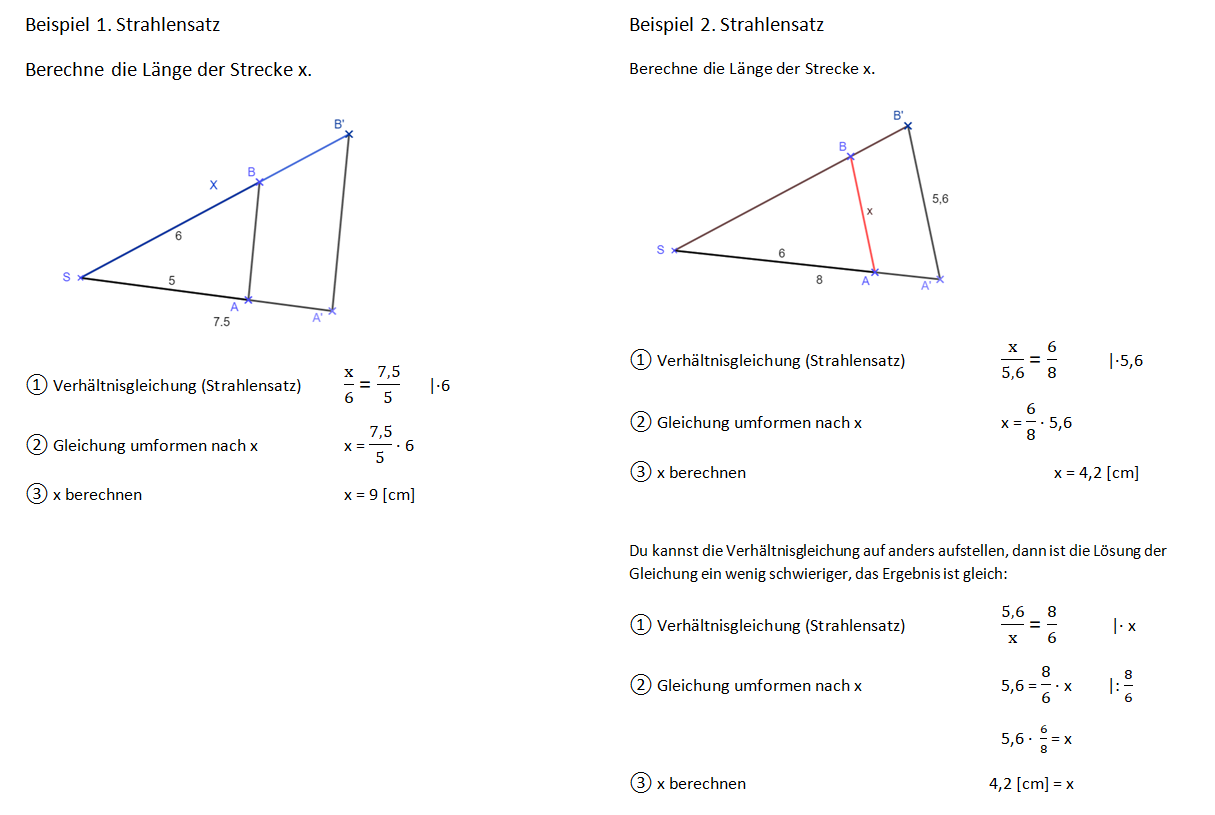
Die nachfolgendne Video zeigt die Strahlensätze in dieser sogenannten x-Figur und Beispiele zu Streckenberechnungen.
Kontrolliere hier deine Ergebnisse der Verhältnisgleichungen zu Aufgabe 4. Stelle dazu mit den Schiebereglern die Länge der Strecken passend ein:

3.1) Die Strahlensätze anwenden
Die Strahlensätze helfen, schwer zugängliche oder weit entfernte Streckenlängen zu bestimmen.
Beispiel: Die Länge eines Sees soll bestimmt werden. Dazu werden drei Strecken an Land gemessen und dann mit dem Strahlensatz die Länge des Sees berechnet.
1. Die Strahlensatzfigur ist in der Skizze gegeben. Wo sind die Strahlen? Wo sind die Parallelen? 2. Verhältnisgleichung: = 3. Gleichung lösen: x = ·120
x = 150
4. Antwort: Der See ist 120m lang.
Welche Größen mussten gemessen werden, um die Höhe des Baumes berechnen zu können?
Zeichne eine passende Strahlensatzfigur in dein Heft und bestimme die Höhe des Baums.