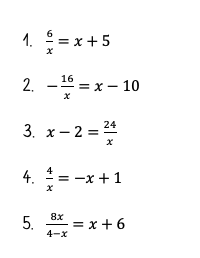|
|
| Zeile 19: |
Zeile 19: |
|
| |
|
|
| |
|
| <nowiki>{{Box|Tipp|Schaut im Buch auf S. 36 und S. 37 die Beispielaufgaben an. </nowiki>Die quadratische Ergänzung funktioniert immer gleich. Wir ergänzen immer auf beiden Seiten der Gleichung <math>\left ( \frac{b}{2} \right )^2</math><nowiki>. b ist dabei die Zahl, die vor dem x steht.|Unterrichtsidee }}</nowiki>
| | {{Box|Tipp|Schaut im Buch auf S. 36 und S. 37 die Beispielaufgaben an. |
| | Die quadratische Ergänzung funktioniert immer gleich. |
| | Wir ergänzen immer auf beiden Seiten der Gleichung <math>\left ( \frac{b}{2} \right )^2</math>. b ist dabei die Zahl, die vor dem x steht.|Unterrichtsidee }} |
|
| |
|
|
| |
|
Version vom 14. Dezember 2019, 14:52 Uhr
Quadratische Gleichungen und Bruchgleichungen
Hier findest du Übungsaufgaben, sowie Erklärungen zu dem Thema Quadratische Gleichungen und Bruchgleichungen.
Unter folgendem Link könnt ihr eintragen, welche Aufgaben ihr in der kommenden Stunde noch üben möchtet
Rein Quadratische Gleichungen
Noch im Aufbau
Gemischt Quadratische Gleichungen
Satz vom Nullprodukt
Quadratische Ergänzung
ACHTUNG! Wenn ihr im Internet nach der quadratischen Ergänzung sucht, findet ihr oft die Ergänzung als Bestandteil von Parabeln. Das haben wir noch nicht gemacht. des Weiteren gibt es zwei Formen der quadratischen Ergänzung. Wir haben bisher nur eine gemacht. Deshalb seid vorsichtig, dass ihr euch nicht selbst verwirrt.
Tipp
Schaut im Buch auf S. 36 und S. 37 die Beispielaufgaben an.
Die quadratische Ergänzung funktioniert immer gleich.
Wir ergänzen immer auf beiden Seiten der Gleichung

. b ist dabei die Zahl, die vor dem x steht.
Beispiel:

Die Zahl, die vor dem x steht (die also mit einem "Mal Zeichen" mit x verbunden ist) ist die 2. Das heißt wir setzen für b die Zahl 2 ein.

Daraus folgt:

Nun entsteht eine Binomische Formel. In diesem Fall die erste. Falls du die binomischen Formeln nicht mehr kennst klicke folgenden Link.
Wir dürfen schreiben:






Lösungsformel
Noch im Aufbau
Bruchgleichungen
Merke
Eine Gleichung, in der Variablen im Nenner vorkommen heißen Bruchgleichungen.
Bruchgleichungen löst man schrittweise:
1. Definitionsmenge bestimmen. (Hier klicken, um mehr über die Definitionsmenge zu erfahren.)
2. Mit einem geeigneten gemeinsamen Nenner multiplizieren.
3. Gleichung durch umformen lösen.
4. Überprüfen, ob die Lösungen in der Definitionsmenge enthalten sind.
Beispiel
1. x1 = 1; x2 = -6
2. x1 = 8; x2 = 2
3. x1 = 6; x2 = -4
4. Keine Lösung
5. x1 = 2; x2 = -12
Unter folgendem Link könnt ihr eintragen, welche Aufgaben ihr in der kommenden Stunde noch üben möchtet
Ähnlichkeit
Vergrößern und Verkleinern
Merke
Eine Figur maßstäblich vergrößern oder verkleinern bedeutet: Alle Seitenlängen werden mit demselben positiven Faktor k multipliziert.
Ist der Faktor k größer als 1, wird die Figur vergrößert.
Ist der Faktor k kleiner als 1, wird die Figur verkleinert.
k ist der Quotient aus der Länge der Bildstrecke und der Länge der Originalstrecke.
Die Winkel bleiben unverändert.
Arbeitsauftrag
Betrachte die Abbildung und verändere Position und Größe der Figur. Die beiden Figuren sind immer ähnlich zueinander. Woran kannst du das erkennen?