Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierungen: Zurückgesetzt Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierungen: Zurückgesetzt Quelltext-Bearbeitung 2017 |
||
| Zeile 14: | Zeile 14: | ||
<ggb_applet id="m2gj2nux" width="859" height="560" border="888888" /> | <ggb_applet id="m2gj2nux" width="859" height="560" border="888888" /> | ||
Applet von C. Buss-Haskert | Applet von C. Buss-Haskert | ||
Oh, verstehe! Wenn du den Lückentext für ein Wiki anpasst, kannst du die runden Klammern direkt im Text verwenden, indem du sie einfach hinzufügst. Hier ist eine angepasste Version des Codes: | |||
```plaintext | |||
{{Box|1=Eigenschaften der Exponentialfunktion|2= | {{Box|1=Eigenschaften der Exponentialfunktion|2= | ||
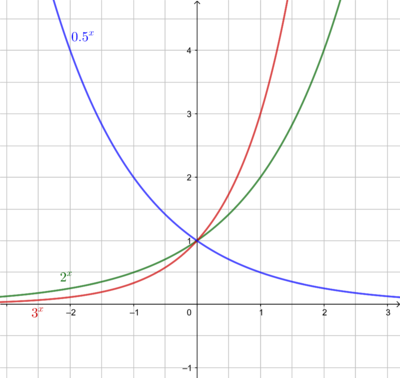
Beschreibe den Verlauf des Graphen der Exponentialfunktion | Beschreibe den Verlauf des Graphen der Exponentialfunktion f(x) = a<sup>x</sup>. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Der Graph verläuft immer '''oberhalb''' der x-Achse. | Der Graph verläuft immer '''oberhalb''' der x-Achse. | ||
Der Graph geht immer durch den Punkt ''' | Der Graph geht immer durch den Punkt '''(0|1)''' | ||
Für | Für a>1 '''steigt''' der Graph (Zunahme), | ||
für | für 0<a<1 '''fällt''' der Graph (Abnahme). | ||
</div> | </div> | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
``` | |||
Mit dieser Schreibweise werden die runden Klammern direkt im Text verwendet, ohne dass zusätzliche Formatierungen erforderlich sind. Dies sollte in einem Wiki-Kontext funktionieren. Gib mir Bescheid, wenn es weitere Fragen oder Anpassungen gibt! 😊 | |||
{{Box|1=Eigenschaften der Exponentialfunktion|2= Beschreibe den Verlauf des Graphen der Exponentialfunktion f(x) = a<sup>x</sup>. | {{Box|1=Eigenschaften der Exponentialfunktion|2= Beschreibe den Verlauf des Graphen der Exponentialfunktion f(x) = a<sup>x</sup>. | ||
Version vom 7. Januar 2025, 15:16 Uhr
Vorwissen
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
4 Die Exponentialfunktion
Originallink https://www.geogebra.org/m/m2gj2nux

Applet von C. Buss-Haskert Oh, verstehe! Wenn du den Lückentext für ein Wiki anpasst, kannst du die runden Klammern direkt im Text verwenden, indem du sie einfach hinzufügst. Hier ist eine angepasste Version des Codes:
```plaintext
```
Mit dieser Schreibweise werden die runden Klammern direkt im Text verwendet, ohne dass zusätzliche Formatierungen erforderlich sind. Dies sollte in einem Wiki-Kontext funktionieren. Gib mir Bescheid, wenn es weitere Fragen oder Anpassungen gibt! 😊
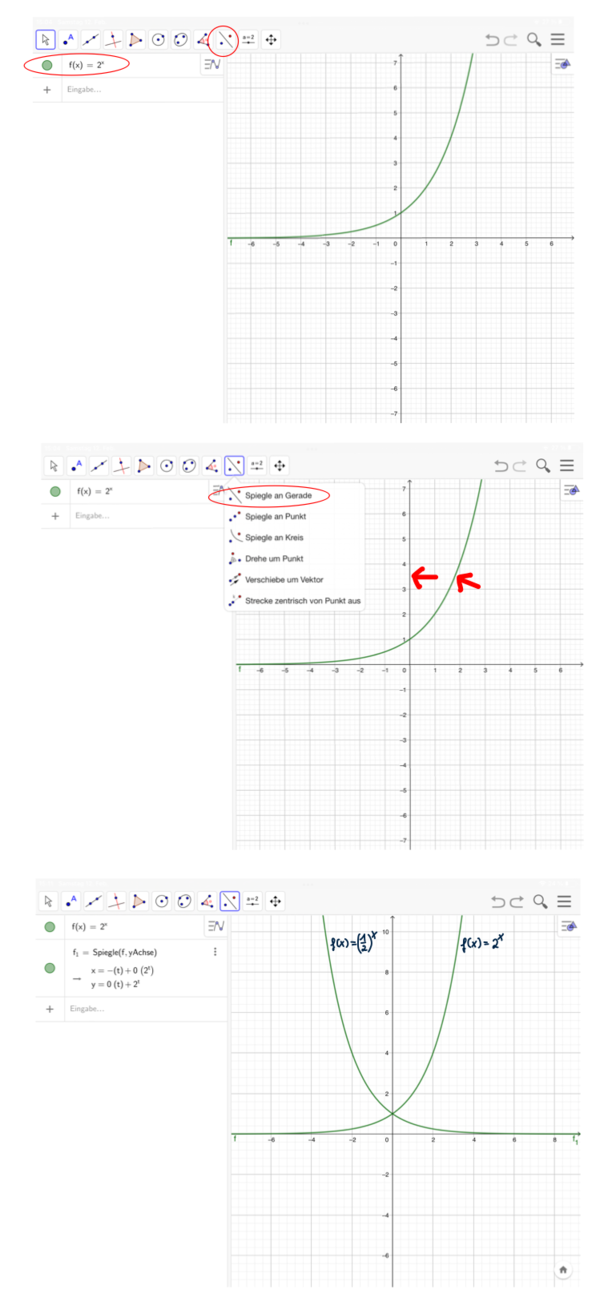
Die Bilderfolge zeigt dir, wie du in GeoGebra Funktionsgraphen an Geraden spiegelst. Wähle das entsprechende Werkzeug und berühre anschließend den Graphen und die y-Achse (rote Pfeile).