Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 337: | Zeile 337: | ||
==3.3 Anwendung des exponentiellen Wachstums: Halbwertszeit und Generationszeit (Verdopplungszeit)== | ==3.3 Anwendung des exponentiellen Wachstums: Halbwertszeit und Generationszeit (Verdopplungszeit)== | ||
Einstieg: evtl. Bierschaumzerfall (Untersuchtung auf [https://www.leifiphysik.de/kern-teilchenphysik/radioaktivitaet-einfuehrung/versuche/bierschaumzerfall leifiphysik]) | Einstieg: evtl. Bierschaumzerfall (Untersuchtung auf [https://www.leifiphysik.de/kern-teilchenphysik/radioaktivitaet-einfuehrung/versuche/bierschaumzerfall leifiphysik]) | ||
{{Box|1=Halbwertszeit|2=Die Halbwertszeit T<sub><math>\tfrac{1}{2}</math></sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge radioaktiven Materials halbiert hat.<br> | {{Box|1=Halbwertszeit|2=Die Halbwertszeit T<sub><math>\tfrac{1}{2}</math></sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge radioaktiven Materials '''halbiert''' hat.<br> | ||
Der Wachstumsfaktor ist also q=100% - 50% = 1 - 0,5 = 0,5 und <br> | Der '''Wachstumsfaktor''' ist also '''q = '''100% - 50% = 1 - 0,5 = '''0,5''' und <br> | ||
die Anzahl n der Zerfallsprozesse wird berechnet mit n = <math>\tfrac{Zeit}{Halbwertszeit}</math>.|3=Kurzinfo}} | die Anzahl '''n der Zerfallsprozesse''' wird berechnet mit n = <math>\tfrac{Zeit}{Halbwertszeit}</math>.|3=Kurzinfo}} | ||
Das nachfolgende Applet stellt den Zerfallsprozess anschaulich dar: | Das nachfolgende Applet stellt den Zerfallsprozess anschaulich dar: | ||
| Zeile 348: | Zeile 348: | ||
<small>Applet von Hegius, Mathezone</small> | <small>Applet von Hegius, Mathezone</small> | ||
{{Box|1=Generationszeit/ Verdopplungszeit|2= Die Generationszeit T<sub>2</sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge / Population verdoppelt hat.<br> | {{Box|1=Generationszeit/ Verdopplungszeit|2= Die Generationszeit T<sub>2</sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge / Population '''verdoppelt''' hat.<br> | ||
Der Wachstumsfaktor ist also q = 100%+100% = 1 + 1 = 2 und <br> | Der '''Wachstumsfaktor''' ist also '''q ='''100%+100% = 1 + 1 = '''2 '''und <br> | ||
die Anzahl n der Generationszeiten wird berechnet mit n = <math>\tfrac{Zeit}{Generationszeit}</math>.|3=Kurzinfo}} | die Anzahl n der Generationszeiten wird berechnet mit n = <math>\tfrac{Zeit}{Generationszeit}</math>.|3=Kurzinfo}} | ||
Das nachfolgende Applet stellt den Verdopplungsprozess anschaulich dar: | Das nachfolgende Applet stellt den Verdopplungsprozess anschaulich dar: | ||
Version vom 7. Januar 2025, 15:42 Uhr
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
3 Exponentielles Wachstum
Prognose für das Jahr 2030: n = 11
W11 = W0 ∙ q11
= 7,70 ∙ 1,02511
Die Gleichung Wn = W0 · qn heißt Exponentialgleichung, da die Variable n im Exponenten steht.
Erinnerung vermehrter/verminderter Grundwert in der Prozentrechnung:
vermehrter Grundert: G+ = G · p+% (mit p+% = 1+p% = q)

Applet von C. Buß-Haskert Originallink https://www.geogebra.org/m/jtgzqdtf
3.1 Exponentielles Wachstum: Beispiele und Anwendungen
3.1.1 Wn gesucht
geg: W0 = 1,38 Mrd.; p% = 0,8% = 0,008, also ist q = 1+0,008 = 1,008; n = 5 (von 2020 - 2025)
ges: W5
Wn = W0 · qn
W5 = 1,38 · 1,0085
= 1,436
Du nutzt folgende Taste beim Taschenrechner, um Exponenten größer als 3 einzugeben (hier z.B. n = 8):

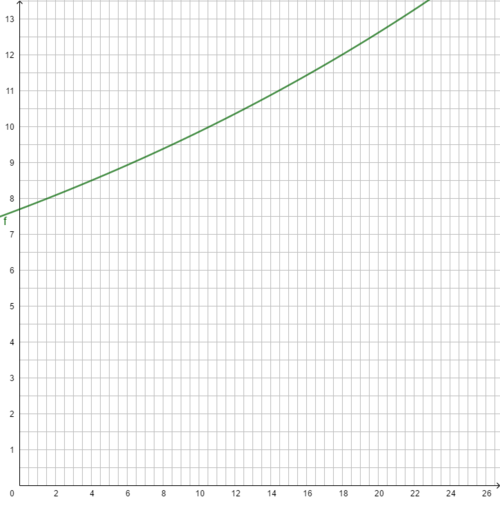
3.1.2 W0 gesucht
geg: W30 = 4,7 Mio km²; p% = -1,7% = -0,017, also ist q = 1-0,017 = 0,983; n = 30
ges: W0
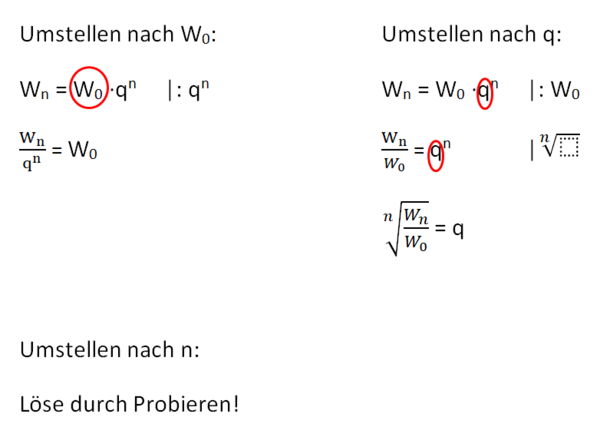
Wn = W0 · qn | : qn
W0 =
W0 =
=
≈ 7,86
3.1.3 q bzw. p% gesucht
geg: W0 = 600 €; W5 = 730 €; n = 5
ges: q bzw. p%
Wn = W0 · qn | : W0
= qn |
= q
1,04 ≈ q
p% = q - 1 = 0,04 = 4%
3.1.4 n gesucht
geg: W0 = 100°C; Wn = 65°C ; p% = -5% = -0,05, also q = 1-0,05 = 0,95
ges: n
Wn = W0 · qn | Löse durch systematisches Probieren (Wertetabelle)
Für n = 1 gilt:
W1 = W0 · q1 |
= 100 · 0,951
= 95 (°C)
...
Für n = 8 gilt:
W8 = W0 · q8 |
= 100 · 0,958
≈ 66,3 (°C)
Für n = 9 gilt:
W9 = W0 · q9 |
= 100 · 0,959
≈ 63,0 (°C)
Du kannst die Lösung auch durch Logarithmieren lösen:
Wn = W0 · qn
65 = 100 · 0,95n |:100
0,65 = 0,95n |log
log0,950,65 = n
8,4 ≈ n
geg: W0 = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3
ges: W1; W2; ...; W5
geg: W0 = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3; Wn = 1200 g
ges: n
Rechne wie in Anwendungsaufgabe 4. Löse durch systematische Probieren.
Lösung:
für n = 6 ist W6 = ... ≈965,4 g
für n = 7 ist W7 = ... ≈ 1254,9 g
geg: W0 = 18700 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009; n = 2 (von 2013 bis 2015)
ges: W2
geg: W2 = 22500 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009
ges: W0 (2013) und W1 (2014)
geg: W0 = 26200 €(im Jahr 2018); p% = 2,3% = 0,023, also q = 1+0,023 = 1,023; n = 5 (von 2018 bis 2023)
ges: W5
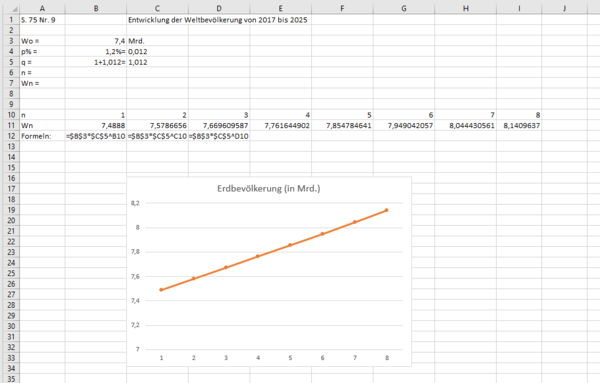
geg: W0 = ... (Bevölkerungszahlen im Jahr 2010); p% = 1,2% = 0,012, also q = 1+0,012= 1,012 usw.; n = 40 (von 2010 bis 2050)
ges: W40
geg: W0 = 100% (Lichtintensität); p% = -11% = -0,11, also q = 1-0,11 = 0,89; n = 10 (in 10m Tiefe)
ges: W10
Rechne wie in Anwendungsaufgabe 1.
Lösung: W10 = ... ≈ 31,2%
geg: Luftdruck in Meereshöhe W0=1013 hPa; Abnahme je 100m p%=-1,23%=-0,0123, also q=1-0,0123 = 0,9877; Höhe des Kilimandscharo 5895m = 58,95· 100 m, also x = 58,95 und des Mt. Everest 8848m = 88,48·100 m, also x = 88,48
ges: Luftdruck auf den Bergen, also Wx
Wx = W0 · qx
= 1013 · 0,987758,95
≈ 488,4 (hPa)
Bestimme zunächst den Luftdruck in 500 m Höhe (also x = 5) und in 841 m Höhe (also x = 8,41). Danach berechne den Unterschied von beiden. dies ist W.
Gib die Funktionsgleichung bei GeoGebra ein. Wx = 1013 · 0,9887x:100
x steht hier für die Höhe, in der der Luftdruck berechnet werden soll.
3.2 Anwendung des exponentiellen Wachstums: Zinseszinsrechnung
Bei diesem Kapitalwachstum handelt es sich um ein exponentielles Wachstum.
geg:K = 7500€; p% = 1,5% = 0,015, also q = 1 + 0,015 =1,015; n = 5
K5 = K0 ∙ q5
= 7500 ∙ 1,0155
a) geg:...
ges: q; Kn
q = 1 + p% = 1 + 0,015 = 1,015
b) geg:...
ges: p%; Kn
p% = q - 1 = 1,035 - 1 = 0,035 = 3,5%
c) geg: ...
ges: K0; p%
d)geg: ...
ges: q und p%
Stelle die Formel nach q um und setzte die gegebene Größen ein. Bestimme so den Wert für q.
e) geg: ...
ges: q; n
q = 1 + p% = ...
Bestimme n durch Probieren.
Rechne zunächst mit einem Betrag von z.B. K0 = 1000€
geg: K0 = 1000€; Kn = 2 ∙ 1000€ = 2000€; p% = 1,8% = 0,018, q = 1 + 0,018 = 1,018
Stelle die passende Gleichung auf und gib diese bei GeoGebra ein. Löse damit Aufgabenteil c) und d),
(Kn=7200∙1,018n
x
Vergleiche die beiden Angebote:
Angebot A:
geg: K0 = 10000€; p% = 2,25% = 0,0225, also q = 1,0225; n = 7 Jahre
ges: Kn
Kn = K0 ∙ qn Setze ein und berechne.
Angebot B:
geg: K0 = 10000€; p% = 1,5% = 0,015, also q = 1,015; n = 7 Jahre; auf das Kapital nach 7 Jahren K7 gibt es zusätzlich 10%.
Kn = K0 ∙ qn Setze ein und berechne.
Berechne dann das Endkapital, indem du auf K7 noch einmal einen Aufschlag von 10% rechnest:
Endkapital KEnde = K7 ∙ 1,1 ...
a) geg: K0 = 2800€; n = 5; K5 = 3607,75€;
ges: Zinssatz p% (Berechne zunächst q und damit dann p%).
b) K0 = 5000€; p% = 4,5 = 0,045, also q = 1,045; Kn = 2 ∙ 5000€ = 10000€ ("verdoppelt")
ges: n
Löse durch Probieren!
c) geg: n = 8 Jahre; p% = 5,25% = 0,0525, also q = 1 + 0,0525 = 1,0525; K8 = 6776,25€
ges: K0
Vergleiche deine Lösungen zu den Aufgaben oben (bunte Mischung)
K0 = 500€; K0 = 4500€
p% = 1,2%; p% = 1%; p% = 3,5%; p% = 5,2%;
q=1,015; q = 1,01; q =1,03
Kn=8079,63€; Kn = 11685,39€; Kn = 11098,45€; Kn = 12208,29€
3.3 Anwendung des exponentiellen Wachstums: Halbwertszeit und Generationszeit (Verdopplungszeit)
Einstieg: evtl. Bierschaumzerfall (Untersuchtung auf leifiphysik)
Das nachfolgende Applet stellt den Zerfallsprozess anschaulich dar:
- Halbwertszeit (Atome)
Direkter Link: https://www.geogebra.org/m/cq62nsqj

Applet von Hegius, Mathezone
Das nachfolgende Applet stellt den Verdopplungsprozess anschaulich dar:
- Generationszeit/ Verdopplungszeit (Bakterien)
Direkter Link: passt das Applet??

Applet von Hegius, R. Schürz
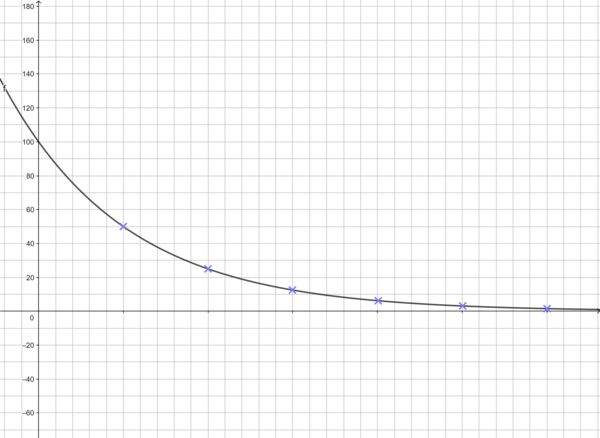
geg: Wismut 210 mit T = 5 Tage; q = 0,5 und Ausgangsmenge W0 = 100g.
Zeit = 30 Tage, in 5 Tagesabschnitten, also für n = 1, 2, 3, 4, 5 und 6
ges: Wertetabelle:
W1 = W0 · 0,51
= 100 · 0,5 = 50 (g)
W2 = W0 · 0,52
= 100 · 0,52 = 25 (g)
W3 = W0 · 0,53
= 100 · 0,53 = 12,5 (g)
...
geg: Radium-229 mit T = 240 s; q = 0,5 und Ausgangsmenge W0 = 48g.
Zeit = 6 Minuten = 360 s
ges: n; Wn
n = = = 1,5
geg: Radium-229 mit T = 240 s; q = 0,5 und Ausgangsmenge W0 = 48mg.
Wn = 1,5 mg
ges: n; t (Zeit)
1,5 = 48 · 0,5n
Löse durch systematisches Probieren.
geg: Generationszeit T2 = 45 Tage; W0 = 10 (Ratten); q = 2; t = 3 Monate = 90 Tage; n = = = 2
geg: Generationszeit T2 = 45 Tage = 1,5 Monate; q = 2; W0 = 10 (Ratten); Wn = 80 Mio;
ges: n; t
geg: n = 23 (wie in Nr. 8b)
geg: q = 2; W0 = 50 Bakterien; T2 = 30 Minuten = 0,5 Stunden; t= 3,5 Stunden; n = = = 7
geg: q = 2; T2 = 3 Wochen; Wn = 100·W0
ges: n; t
Wn = W0·qn | Setze q = 2 und Wn = 100·W0 ein
Löse durch systematisches Probieren.
ges: n; Wn
n = ≈ 6,4
Wn = W0 · qn
geg: W0 = 400; W18,8 = 2·400 = 800; n = 18,8
ges: q
Wn = W0 · qn
800 = 400 · q18,8 |:400
2 = q18,8 |
= q
1,038 ≈ q
geg: W0 = 400; n = 2h = 120min; q = 1,038
ges: Wn
geg: W0 = 100% (die gesamte Menge des Stoffe ist noch da); W6 = 100% - 34% = 66%; n = 6
ges: q
W6 = W0 · q6 | Umstellen nach q
= q
= q
0,933 ≈ q
Nun berechne die Halbwertszeit:
geg: W0 = 100%; Wn = 50%; q = 0,933
ges: n
Wn = W0 · qn
0,5 = 1 · 0,993n
Löse durch Probieren.
Für n = 9 gilt: W9 ≈ 0,54
Für n = 10 gilt: W10 ≈ 0,4998
geg: W0 = 100%; W24 = 300% (verdreifacht); n = 24
ges: q (prozentuales Wachstum pro Tag); p%
...
Einschub: Logarithmieren
Ist beim exponentiellen Wachstum der Exponent n gesucht, kannst du diesen Wert durch systematisches Probieren erhalten. Eine genauere Möglichkeit ist das Logarithmieren.
Falls du einen Taschenrechner nutzt, der diese Möglichkeit nicht hat, tippe wie folgt:
x =