Geometrie im Dreieck/Auf den Spuren der Winkel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (155 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Kapitel-Informationskästchen= | ==Kapitel-Informationskästchen== | ||
{{Box | {{Box | ||
| Zeile 5: | Zeile 5: | ||
|2=In diesem Lernpfadkapitel beschäftigen wir uns mit den verschiedenen Winkelarten: dem Neben-, Scheitel-, Stufen- und Wechselwinkel. | |2=In diesem Lernpfadkapitel beschäftigen wir uns mit den verschiedenen Winkelarten: dem Neben-, Scheitel-, Stufen- und Wechselwinkel. | ||
Du hast noch Unsicherheiten, wann welcher Winkel vorliegt? | Du hast noch Unsicherheiten, wann welcher Winkel vorliegt? Du hast Schwierigkeiten sie zu erkennen? Oder die nützlichen Eigenschaften, die mit den verschiedenen Winkeln einhergehen, sind dir noch nicht vollends bewusst? Dann bist du hier genau richtig. Wir lernen das gemeinsam. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 14: | Zeile 14: | ||
Viel Erfolg! | Viel Erfolg! | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
==Freds Herausforderung== | |||
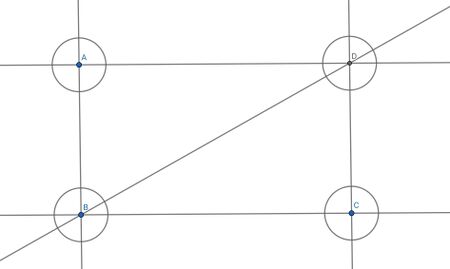
Fred nimmt gerade das Thema "Winkel" im Mathematikunterricht durch. Im Sportunterricht erkennt Fred in einer Konstruktion verschiedene Dreiecke und Winkel. Freds Mathematik- und Sportlehrerin schlägt ihm vor, dass er seine Mathematiknote verbessern kann, wenn er die Winkel in der Konstruktion bestimmen kann. Da Fred nicht ganz zufrieden mit seiner Mathematiknote ist und diese gerne verbessern würde, möchte er die Winkel der Konstruktion nun bestimmen. | |||
[[Datei:Kastenkombio.jpg|thumb|Kastenkombio|zentriert|mini|450x450px| ]] | |||
Um die Winkelgrößen zu bestimmen, fertigt er eine Zeichnung an. | |||
[[Datei:FredsZeichnung.jpg|thumb|FredsZeichnung|zentriert|mini|450x450px| Freds Zeichnung.]] | |||
Denkst du Freds Zeichnung ist passend für das Problem? Halte deine Überlegungen fest und begründe sie. Die Auflösung erhältst du nach Bearbeitung des Kapitels. | |||
==Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen== | ==Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen== | ||
{{Box|Aufgabe 1|Teste dein Wissen zu den verschiedenen Winkelarten. Ordne die Bilder der Winkel den richtigen Bezeichnungen zu. | |||
<iframe src="https://learningapps.org/watch?v=pwiqmvfdj24" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
Dir ist die Zuordnung nicht so leicht gefallen? Dann schaue dir die folgenden Merksätze zu den Winkelarten an. | |||
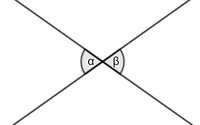
{{Box|Merksätze|{{Lösung versteckt|1=[[Datei:Scheitelwinkel.jpg|rechts|200x200px]] | |||
An zwei Geraden, die sich schneiden, nennt man gegenüberliegende Winkel '''Scheitelwinkel'''. Die Winkel sind gleich groß. | |||
In der Abbildung: α und β sind Scheitelwinkel und es gilt α <math>=</math> β. |2=Merksatz Scheitelwinkel|3=Merksatz Scheitelwinkel verbergen}}{{Lösung versteckt|1=[[Datei:Nebenwinkel.jpg|rechts|130x130px]] | |||
An zwei Geraden, die sich schneiden, nennt man nebeneinanderliegende Winkel '''Nebenwinkel'''. Nebenwinkel ergeben zusammen 180°. | |||
In der Abbildung: α und β sind Nebenwinkel und es gilt α+β <math>=</math> 180°.|2=Merksatz Nebenwinkel|3=Merksatz Nebenwinkel verbergen}} | |||
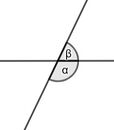
{{Lösung versteckt|1=[[Datei:Stufenwinkel.jpg|rechts|200x200px]] | |||
An zwei parallelen Geraden, die von einer weiteren Geraden geschnitten werden, nennt man Winkel, die in Stufen angeordnet sind, '''Stufenwinkel'''. | |||
Die Winkel sind gleich groß. | |||
In der Abbildung: α und β sind Scheitelwinkel und es gilt α = β.|Merksatz | In der Abbildung: α und β sind Stufenwinkel und es gilt α<math>=</math> β.|2=Merksatz Stufenwinkel|3=Merksatz Stufenwinkel verbergen}}{{Lösung versteckt|1=[[Datei:Wechselwinkel.jpg|rechts|180x180px]] | ||
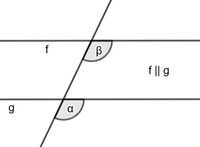
An zwei parallelen Geraden, die von einer weiterer Geraden geschnitten werden, erhält man '''Wechselwinkel''', indem man erst den Stufenwinkel und anschließend davon den Scheitelwinkel bestimmt. Auch für Wechselwinkel gilt, dass sie gleich groß sind. | |||
In der Abbildung: α und β sind Wechselwinkel und es gilt α<math>=</math> β.|2=Merksatz Wechselwinkel|3=Merksatz Wechselwinkel verbergen}}|Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | }} | ||
==Aufgabe 2: Winkelgrößen bestimmen== | |||
==Aufgabe 2: Winkelgrößen bestimmen == | |||
{{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen und begründe | '''Hinweis:''' Wähle eine der drei Aufgaben aus. | ||
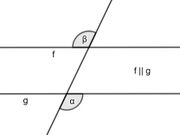
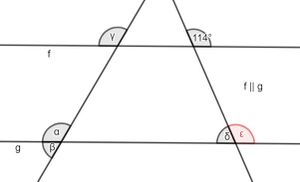
{{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen ohne zu messen und begründe mithilfe der Winkelarten, wie du auf die Lösung gekommen bist. | |||
[[Datei:Winkelgröße 1.jpg|zentriert|mini]] | [[Datei:Winkelgröße 1.jpg|zentriert|mini]] | ||
| Zeile 31: | Zeile 72: | ||
{{Lösung versteckt|1= '''β=120°''' | {{Lösung versteckt|1= '''β=120°''' | ||
mögliche | mögliche Begründungen: | ||
: 1. β ist Stufenwinkel zum Winkel 120°. Da Stufenwinkel gleich groß sind, gilt β=120°. | : 1. β ist Stufenwinkel zum Winkel 120°. Da Stufenwinkel gleich groß sind, gilt β=120°. | ||
: 2. Falls δ=120° schon bestimmt wurde: β=120°, da β und δ Wechselwinkel sind und diese gleich groß sind. | : 2. Falls δ=120° schon bestimmt wurde: β=120°, da β und δ Wechselwinkel sind und diese gleich groß sind. | ||
| Zeile 52: | Zeile 93: | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
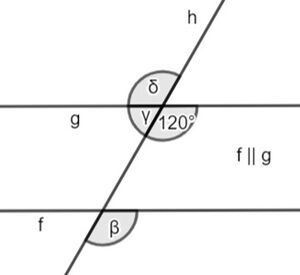
[[Datei:Winkelgröße 2.jpg|zentriert|mini|450x450px]] | {{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen ohne zu messen und begründe mithilfe der Winkelarten, wie du auf die Lösung gekommen bist. | ||
[[Datei:Winkelgröße 2 neu.jpg|zentriert|mini|450x450px]] | |||
{{Lösung versteckt|1= '''α=70°''' | {{Lösung versteckt|1= '''α=70°''' | ||
| Zeile 90: | Zeile 131: | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
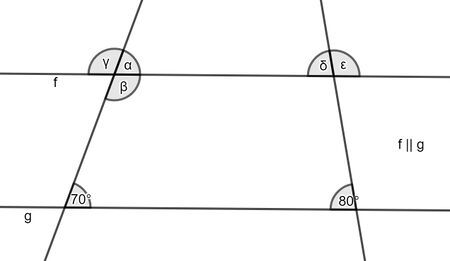
{{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen und begründe | {{Box|Aufgabe 2: Winkelgrößen bestimmen|Bestimme die Winkelgrößen ohne zu messen und begründe mithilfe der Winkelarten, wie du auf die Lösung gekommen bist. | ||
[[Datei:Winkelgröße 3.1.jpg|zentriert|mini|450x450px|Winkel α ist doppelt so groß wie Winkel β.]] | [[Datei:Winkelgröße 3.1.jpg|zentriert|mini|450x450px|Winkel α ist doppelt so groß wie Winkel β.]] | ||
| Zeile 119: | Zeile 160: | ||
== Aufgabe 3: Wer bin ich? == | ==Aufgabe 3: Wer bin ich?== | ||
{{Box|Aufgabe 3: Winkelarten|Mein Winkel, der genau neben mir liegt, und ich bilden gemeinsam eine gestreckte Linie. Wir ergänzen uns immer zu einem Halbkreis. Wer bin ich? | |||
Mein | {{Lösung versteckt|1=Je größer mein Winkel, der genau neben mir liegt, ist, desto kleiner bin ich.|2=Tipp 1|3=Tipp 1}} | ||
{{ | {{Lösung versteckt|1=Mein Winkel, der genau neben mir liegt, und ich ergeben gemeinsam 180°. Wenn er beispielsweise 70° aufweist, besitze ich 110°.|2=Tipp 2|3=Tipp 2}} | ||
=== | {{Lösung versteckt|1=Ich bin der Nebenwinkel.|2=Lösung|3=Lösung}} | ||
=== | |||
=== | |||
Mein Partner und ich sind uns sehr ähnlich. Wir berühren uns im Schnittpunkt der Geraden. Wer bin ich? | |||
{{Lösung versteckt|1=Mein Partner und ich haben immer die selbe Winkelgröße.|2=Tipp 1|3=Tipp 1}} | |||
{{Lösung versteckt|1=Wir liegen zwar nicht nebeneinander, dafür aber direkt gegenüber.|2=Tipp 2|3=Tipp 2}} | |||
{{Lösung versteckt|1=Ich bin der Scheitelwinkel.|2=Lösung|3=Lösung}} | |||
Mein Partner und ich sind nie auf der gleichen Seite. Vielleicht liegt es daran, dass wir uns stets auf einer unterschiedlichen Geraden (parallel zueinander) befinden. Wer bin ich? | |||
{{Lösung versteckt|1=Ich entstehe, wenn eine dritte Gerade zwei parallele Geraden schneidet.|2=Tipp 1|3=Tipp 1}} | |||
{{Lösung versteckt|1=Mein Partner und ich haben die gleiche Winkelgröße.|2=Tipp 2|3=Tipp 2}} | |||
{{Lösung versteckt|1=Ich bin der Wechselwinkel.|2=Lösung|3=Lösung}} | |||
Mein Partner und ich sind stets auf der gleichen Seite, obwohl wir uns auf unterschiedlichen Geraden (parallel zueinander) befinden. Wer bin ich? | |||
{{Lösung versteckt|1=Ich entstehe, wenn eine dritte Gerade zwei parallele Geraden schneidet.|2=Tipp 1|3=Tipp 1}} | |||
{{Lösung versteckt|1=Mein Partner und ich haben die gleiche Winkelgröße.|2=Tipp 2|3=Tipp 2}} | |||
{{Lösung versteckt|1=Ich bin der Stufenwinkel.|2=Lösung|3=Lösung}}|Arbeitsmethode|Farbe | |||
| Farbe = #CD2990 | |||
}} | |||
==Aufgabe 4: Winkel in der Sporthalle== | ==Aufgabe 4: Winkel in der Sporthalle== | ||
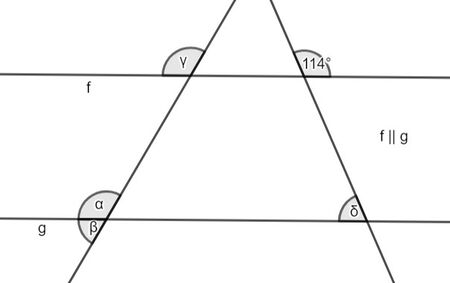
{{Box|Aufgabe 4.1: Winkel berechnen|Wir nehmen an, dass Freds Zeichnung aus dem Einstieg das Problem aus dem Sportunterricht akkurat beschreibt. Berechne die fehlenden Winkel aus der Zeichnung. | |||
[[Datei:Geoge2.jpg|thumb|Geoge2|zentriert|mini|450x450px| ]] | |||
{{ | {{ | ||
Lösung versteckt| | Lösung versteckt|1= | ||
'''α=90°''' | |||
|Lösung|Lösung verbergen | |||
,da die Nebenwinkel zu diesem alle rechte Winkel sind (90°) muss die Winkelgröße von α auch 90° sein. | |||
'''β=90°''' | |||
,da der Scheitelwinkel zu β 90° groß ist muss β=90° gelten. | |||
'''β'=60°''' | |||
,da der Scheitelwinkel zu β' 60° groß ist muss β'=60° gelten. | |||
'''ε=30°''' | |||
,da der Scheitelwinkel zu ε 30° groß ist muss ε=30° gelten. | |||
'''γ=90°''' | |||
,da die Nebenwinkel zu diesem alle rechte Winkel sind (90°) muss die Winkelgröße von γ auch 90° sein. Genau wie bei α. | |||
'''δ=60°''' | |||
,da der Scheitelwinkel zu δ 60° groß ist muss δ=60° gelten. | |||
'''δ'=90°''' | |||
,da der Scheitelwinkel zu δ' 90° groß ist muss δ'=90° gelten. | |||
'''τ=30°''' | |||
,da der Scheitelwinkel zu τ 30° groß ist muss τ=30° gelten. | |||
|2=Lösung|3=Lösung verbergen | |||
}}|Arbeitsmethode | }}|Arbeitsmethode | ||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | }} | ||
{{Box|Aufgabe 2: | |||
Nachdem du alle Aufgaben bis hier bereits erfolgreich gelöst hast, versuche Fred in der folgenden Aufgabe dabei zu unterstützen, seine Note zu verbessern. | |||
{{Box|Aufgabe 4.2: Berücksichtigung der Voraussetzungen|Freds Lehrerin will ihm die bessere Note noch nicht geben, da er eine wichtige Sache noch nicht berücksichtigt hat. Überlege ein weiteres Mal, ob Freds Herangehensweise an das Problem sinnvoll ist. Notiere deine Überlegungen, vergleiche sie mit deinen Notizen vom Anfang und gleiche sie mit der Lösung ab. | |||
[[Datei:Kastenkombio.jpg|thumb|Kastenkombio|zentriert|mini|450x450px| ]] | |||
{{ | |||
Lösung versteckt|Überlege, ob die Geraden aus Freds Zeichnung genau den Sportgeräten entsprechen.| | |||
Erster Tipp | |||
|Tipp verbergen | |||
}} | |||
{{ | {{ | ||
Lösung versteckt| | Lösung versteckt| | ||
Tipp | Sind Bank und Boden, sowie Kasten und Sprossenwand parallel zueinander?| | ||
Zweiter Tipp | |||
|Tipp verbergen | |Tipp verbergen | ||
}} | }} | ||
{{ | {{ | ||
Lösung versteckt| | Lösung versteckt|1= | ||
Lösung | Fred hat bei seiner Zeichnung nicht darauf geachtet, ob die obere Bank wirklich parallel zum Boden ist. Da das nicht der Fall ist ist Freds Zeichnung nicht genau und er kann die Winkel nicht ideal berechnen.| | ||
2=Lösung| | |||
3=Lösung verbergen | |||
}}|Arbeitsmethode| | }}|Arbeitsmethode| | ||
}} | }} | ||
Hier kommst du zurück zur Startseite des Kapitels:{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Geometrie_im_Dreieck}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 7. Dezember 2024, 08:54 Uhr
Kapitel-Informationskästchen
Freds Herausforderung
Fred nimmt gerade das Thema "Winkel" im Mathematikunterricht durch. Im Sportunterricht erkennt Fred in einer Konstruktion verschiedene Dreiecke und Winkel. Freds Mathematik- und Sportlehrerin schlägt ihm vor, dass er seine Mathematiknote verbessern kann, wenn er die Winkel in der Konstruktion bestimmen kann. Da Fred nicht ganz zufrieden mit seiner Mathematiknote ist und diese gerne verbessern würde, möchte er die Winkel der Konstruktion nun bestimmen.
Um die Winkelgrößen zu bestimmen, fertigt er eine Zeichnung an.
Denkst du Freds Zeichnung ist passend für das Problem? Halte deine Überlegungen fest und begründe sie. Die Auflösung erhältst du nach Bearbeitung des Kapitels.
Aufgabe 1: Zuordnungen von Begriffen zu Abbildungen
Dir ist die Zuordnung nicht so leicht gefallen? Dann schaue dir die folgenden Merksätze zu den Winkelarten an.
Aufgabe 2: Winkelgrößen bestimmen
Hinweis: Wähle eine der drei Aufgaben aus.
Aufgabe 3: Wer bin ich?
Aufgabe 4: Winkel in der Sporthalle
Nachdem du alle Aufgaben bis hier bereits erfolgreich gelöst hast, versuche Fred in der folgenden Aufgabe dabei zu unterstützen, seine Note zu verbessern.
Hier kommst du zurück zur Startseite des Kapitels: