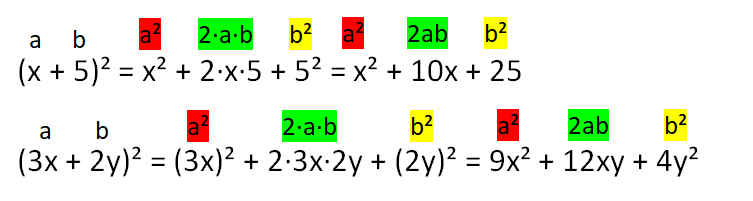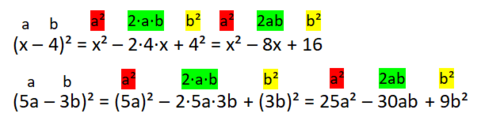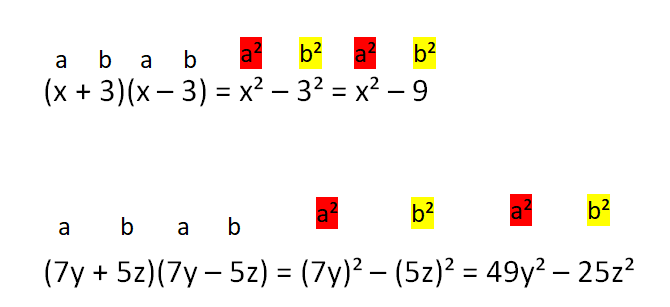Benutzer:L.hodankov/Binomische Formeln: Unterschied zwischen den Versionen
(Inhalte übernommen und angepasst) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule [[https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Terme(mit_Klammern)/Binomische_Formeln]]. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA. | |||
Herzlichen Dank! | |||
SEITE IM AUFBAU! | |||
===Binomische Formeln=== | ===Binomische Formeln=== | ||
Die binomische Formeln sind drei Sonderfälle bei der Multiplikation von Summen. Die Ergebnisse lassen sich hier leicht zusammenfassen und so die ausführlichen Berechnungen abkürzen. | Die binomische Formeln sind drei Sonderfälle bei der Multiplikation von Summen. Die Ergebnisse lassen sich hier leicht zusammenfassen und so die ausführlichen Berechnungen abkürzen. | ||
| Zeile 28: | Zeile 34: | ||
{{LearningApp|app=pwbnw837j19|width=100%|height=600px}}|2= Tipp Quadratzahlen|3=Verbergen}} | {{LearningApp|app=pwbnw837j19|width=100%|height=600px}}|2= Tipp Quadratzahlen|3=Verbergen}} | ||
{{LearningApp|app=p7ieycjz519|width=100%|height=400px}} | {{LearningApp|app=p7ieycjz519|width=100%|height=400px}} | ||
{{LearningApp|app=pb65n03bk20|width=100%|height=400px}} | {{LearningApp|app=pb65n03bk20|width=100%|height=400px}} | ||
{{LearningApp|app=pxb2hozmt22|width=100%|height=400px}} | |||
====2. binomische Formel==== | ====2. binomische Formel==== | ||
| Zeile 57: | Zeile 60: | ||
{{Box|Übung 2: 2. binomische Formel|Bearbeite die nachfolgenden LearningApps.|Üben}} | {{Box|Übung 2: 2. binomische Formel|Bearbeite die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pwvujeibn19|width=100%|height=400px}} | {{LearningApp|app=pwvujeibn19|width=100%|height=400px}} | ||
| Zeile 68: | Zeile 71: | ||
<ggb_applet id="t6syugs7" width="950" height="550" border="888888" /> | <ggb_applet id="t6syugs7" width="950" height="550" border="888888" /> | ||
<small>Applet von Thorsten Glaser</small> | <small>Applet von Thorsten Glaser</small> | ||
| Zeile 89: | Zeile 91: | ||
{{LearningApp|app=pw4x96c9c19|width=100%|height=400px}} | {{LearningApp|app=pw4x96c9c19|width=100%|height=400px}} | ||
{{LearningApp|app=ppj4v8caa20|width=100%|height=400px}} | {{LearningApp|app=ppj4v8caa20|width=100%|height=400px}} | ||
{{Box|Übung 5: 3. binomische Formel|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse die Klammern mithilfe der 3. binomischen Formeln auf. | |||
* S. 163, Nr. 3 | |||
* S. 163, Nr. 4 | |||
* S. 163, Nr. 5. |Üben}} | |||
====Zusammenfassung==== | ====Zusammenfassung==== | ||
| Zeile 100: | Zeile 107: | ||
{{#ev:youtube|EYbvhWEG6kE|800|center}} | {{#ev:youtube|EYbvhWEG6kE|800|center}} | ||
====Vermischte Übungen zu den binomischen Formeln==== | ====Vermischte Übungen zu den binomischen Formeln==== | ||
{{Box|Übung | {{Box|Übung 6|Löse auf der Seite realmath so viele Aufgaben, dass du die 300 Punkte-Marke knackst. | ||
* [https://realmath.de/Neues/Klasse8/binome/binomei01.php Übung Level 1 (realmath)] | * [https://realmath.de/Neues/Klasse8/binome/binomei01.php Übung Level 1 (realmath)] | ||
* [https://www.realmath.de/Neues/Klasse8/binome/binomevar02a-2.php Level 2 (realmath)] | * [https://www.realmath.de/Neues/Klasse8/binome/binomevar02a-2.php Level 2 (realmath)] | ||
|Üben}} | |Üben}} | ||
{{Box|Übung | {{Box|Übung 7|Bearbeite die nachfolgenden LearningApps und Quizze.|Üben}} | ||
{{LearningApp|app=7804644|width=100%|height=600px}} | {{LearningApp|app=7804644|width=100%|height=600px}} | ||
{{LearningApp|app=pcuwev2x319|width=100%|height=600px}} | {{LearningApp|app=pcuwev2x319|width=100%|height=600px}} | ||
{{LearningApp|app=padiizght19|width=100%|height=400px}} | {{LearningApp|app=padiizght19|width=100%|height=400px}} | ||
Übung für Fortgeschrittene: | |||
{{h5p-zum|id=23962|heigth=800px}} | {{h5p-zum|id=23962|heigth=800px}} | ||
(Quizz von B. Lachner) | (Quizz von B. Lachner) | ||
{{Box|Übung | {{Box|Übung 8|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen in dein Heft. | ||
* S. | * S. 164, Nr. 1 | ||
* S. | * S. 164, Nr. 2 | ||
* S. | * S. 164, Nr. 3 | ||
* S. | * S. 164, Nr. 5. |Üben}} | ||
{{Lösung versteckt|Löse Nr. | {{Lösung versteckt|Löse Nr. 5 schrittweise:<br> | ||
Wende zuerst die binomischen Formeln an. Prüfe dann, ob zum Auflösen der Klammer noch ein weitere Schritt notwendig ist (wenn z.B. ein Minuszeichen vor der Klammer steht). Fasse danach zusammen.|1.Tipp zu Nr. | Wende zuerst die binomischen Formeln an. Prüfe dann, ob zum Auflösen der Klammer noch ein weitere Schritt notwendig ist (wenn z.B. ein Minuszeichen vor der Klammer steht). Fasse danach zusammen.|1.Tipp zu Nr. 5|Verbergen}} | ||
=====Übung: Quadratzahlen und besondere Produkte mit den binomischen Formeln berechnen===== | =====Übung: Quadratzahlen und besondere Produkte mit den binomischen Formeln berechnen===== | ||
| Zeile 146: | Zeile 153: | ||
{{LearningApp|app=p3tbprpfk19|width=100%|height=400px}} | {{LearningApp|app=p3tbprpfk19|width=100%|height=400px}} | ||
{{LearningApp|app=p1segcy2j19|width=100%|height=400px}} | {{LearningApp|app=p1segcy2j19|width=100%|height=400px}} | ||
| Zeile 160: | Zeile 161: | ||
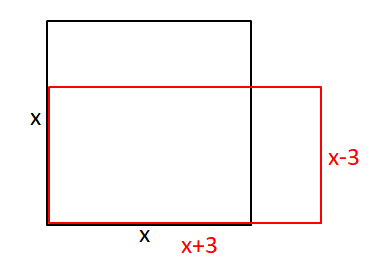
{{Lösung versteckt|Benenne die Länge des quadratischen Grundstückes mit x.<br>Nun hilft eine Skizze:[[Datei:Skizze zum Grundstückstausch.png|rahmenlos|600px]]|Tipp 1|Verbergen}} | {{Lösung versteckt|Benenne die Länge des quadratischen Grundstückes mit x.<br>Nun hilft eine Skizze:[[Datei:Skizze zum Grundstückstausch.png|rahmenlos|600px]]|Tipp 1|Verbergen}} | ||
{{Lösung versteckt|Schau das Video an und übertrage die Idee auf die Aufgabe.{{#ev:youtube|2_bwIaC66AU|500|center}}|Tipp 2|Verbergen}} | {{Lösung versteckt|Schau das Video an und übertrage die Idee auf die Aufgabe.{{#ev:youtube|2_bwIaC66AU|500|center}}|Tipp 2|Verbergen}} | ||
Aktuelle Version vom 6. Mai 2025, 20:46 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule [[1]]. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
SEITE IM AUFBAU!
Binomische Formeln
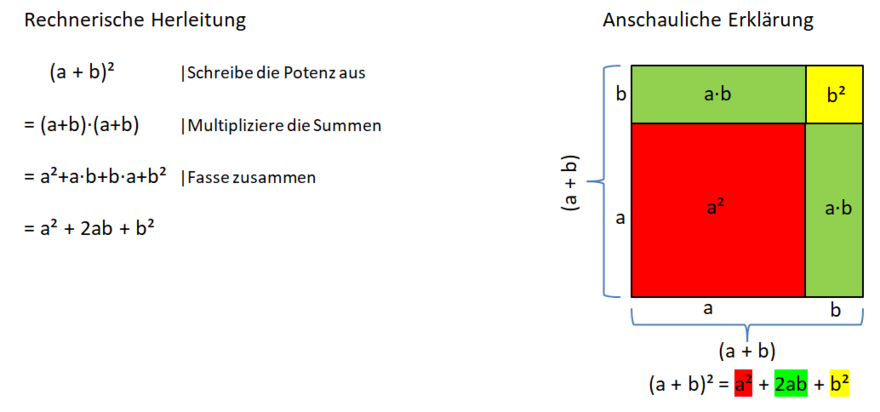
Die binomische Formeln sind drei Sonderfälle bei der Multiplikation von Summen. Die Ergebnisse lassen sich hier leicht zusammenfassen und so die ausführlichen Berechnungen abkürzen.
Durch entsprechende Figuren lassen sie sich auch gut anschaulich erklären.
1. binomische Formel
Herleitung der 1. binomischen Formel

Beispiele:
Übung
Du musst die Quadratzahlen beherrschen! Erinnerung:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400
25² = 625
2. binomische Formel
Herleitung der 2. binomischen Formel
Das GeoGebra-Applet leitet anschaulich die 2. binomische Formel her. Erkläre deinem Partner die einzelnen Schritte.

Übung
Kontrolliere deine Lösungen (als Variablen sind nur x und y erlaubt):

Applet von Thorsten Glaser
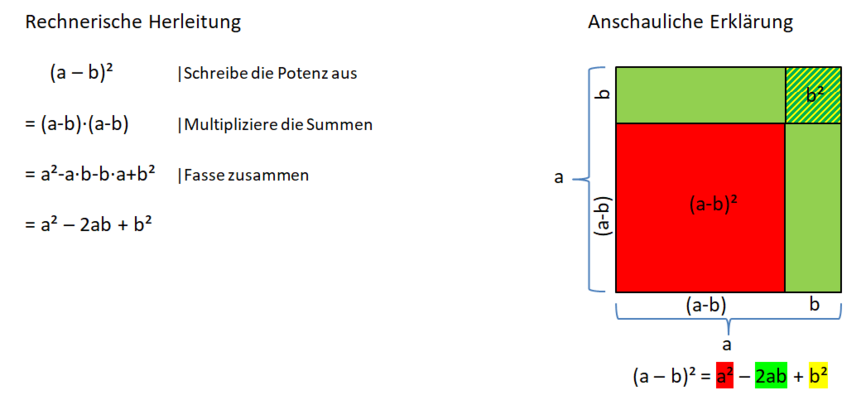
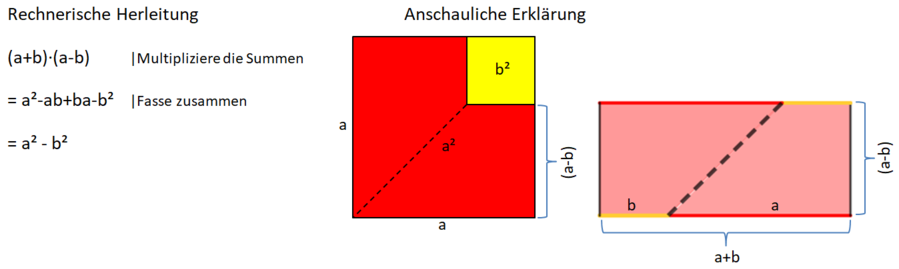
3. binomische Formel
Herleitung der 3. binomischen Formel
Das GeoGebra-Applet leitet anschaulich die 3. binomische Formel her. Erkläre deinem Partner die einzelnen Schritte.

Übung
Zusammenfassung

Das nachfolgende Video fasst die binomischen Formeln noch einmal zusammen.
Nun hast du alle drei binomischen Formeln kennengelernt. Höre das Lied dazu an, dann kannst du dir die Formeln gut merken (es ist ein Ohrwurm!😉).
Vermischte Übungen zu den binomischen Formeln
Übung für Fortgeschrittene:
(Quizz von B. Lachner)
Löse Nr. 5 schrittweise:
Übung: Quadratzahlen und besondere Produkte mit den binomischen Formeln berechnen
Die 1. und 2. binomische Formel helfen beim Berechnen von größeren Quadratzahlen.
Beispiele:
46² = (40+6)²
=40² + 2∙40∙6 + 6²
=1600 + 480 + 36
=2116
39² = (40-1)²
=40² - 2∙40∙1 + 1²
=1600 - 80 + 1
=1521
63 ∙ 57 = (60+3)∙(60-3)
=60² - 3²
=3600 - 9
=3591