Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/Berechnen relativer Häufigkeiten mit Baumdiagrammen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 14: | Zeile 17: | ||
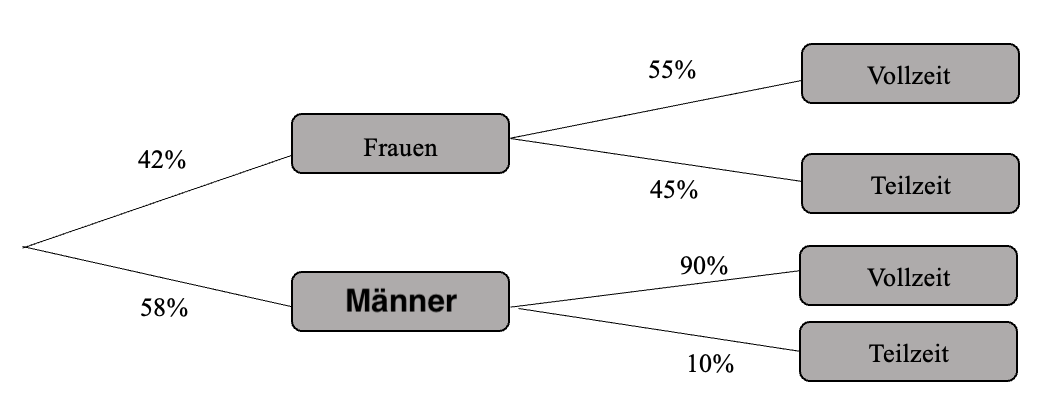
<big>Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.</big> | <big>Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.</big> | ||
[[Datei:Baumdiagramm relative Häufigkeit.png|center]] | [[Datei:Baumdiagramm relative Häufigkeit v2.png|center]] | ||
| Zeile 41: | Zeile 44: | ||
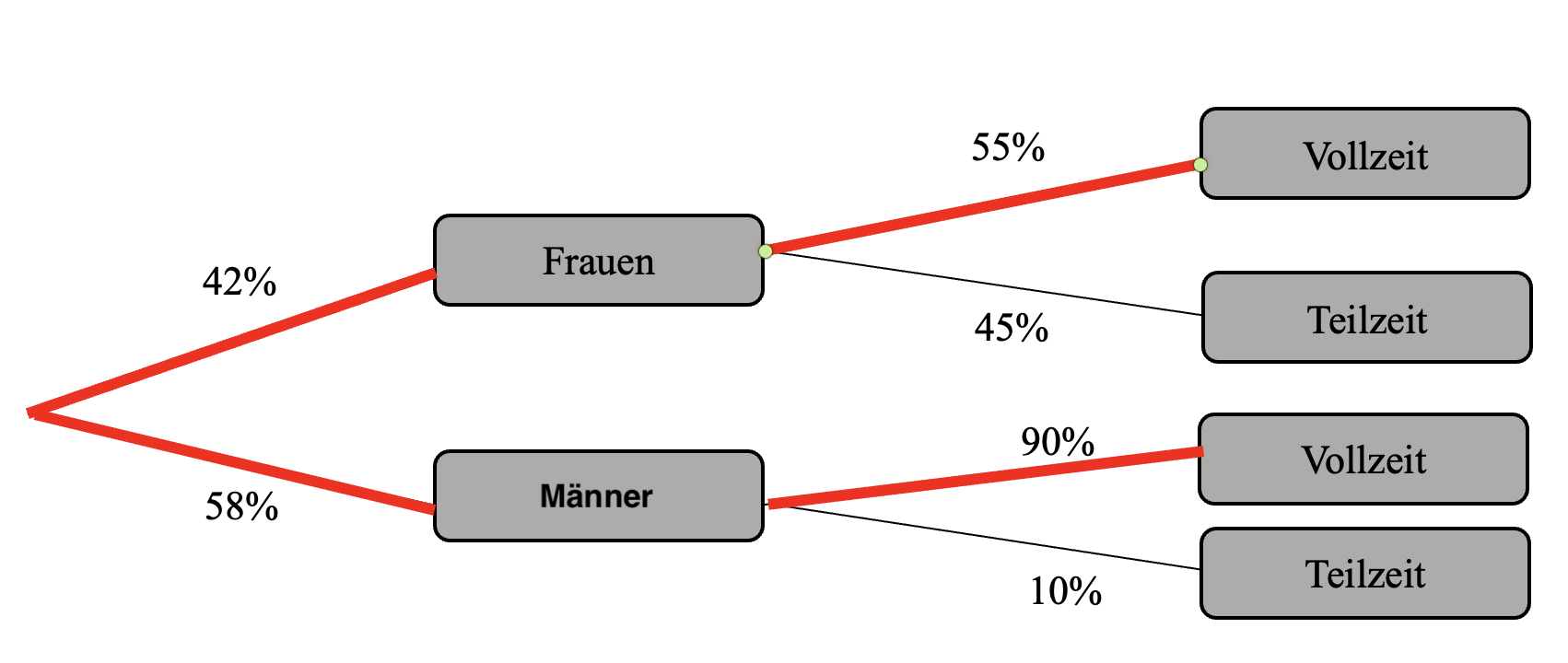
Um die relative Häufigkeit auszurechnen, musst du dir überlegen, welche Ergebnisse (Pfade) auf dein Ereignis passen. Anschließend wendest du wie gewohnt die Produkt- und Summenregel an. | Um die relative Häufigkeit auszurechnen, musst du dir überlegen, welche Ergebnisse (Pfade) auf dein Ereignis passen. Anschließend wendest du wie gewohnt die Produkt- und Summenregel an. | ||
[[Datei:Baumdiagramm relative Häufigkeit | [[Datei:Baumdiagramm relative Häufigkeit Lösung v2.png|center]] | ||
| Zeile 57: | Zeile 60: | ||
'''<big>P(E) = P(Frauen,Vollzeit) | '''<big>P(E) = P(Frauen,Vollzeit) + P(Männer, Vollzeit) = 23,1% + 52,2% = 75,3%</big>''' | ||
| Zeile 74: | Zeile 77: | ||
S.189, Nr.3 | S.189, Nr.3 | ||
S.194, Nr.6 a) und b) | S.194, Nr.6 a) und b) | ||
|Üben}} | |Üben}} | ||
Aktuelle Version vom 25. September 2023, 08:21 Uhr
Beispiel:
Immer mehr Menschen die Arbeiten haben einen Teilzeitjob. Vor allem Frauen arbeiten häufig in Teilzeit. Eine Befragung ergab das nebenstehende Baumdiagramm.
Um die relative Häufigkeit auszurechnen, musst du dir überlegen, welche Ergebnisse (Pfade) auf dein Ereignis passen. Anschließend wendest du wie gewohnt die Produkt- und Summenregel an.
Wie du siehst passende die Ergebnisse (Frauen,Vollzeit) und (Männer, Vollzeit)
Zuerst wenden wir die Produktregel an:
P(Frauen, Vollzeit) = 0,42 ⋅ 0,55 = 0,231 = 23,1%
P(Männer, Vollzeit) = 0,58 ⋅ 0,9 = 0,522 = 52,2%
Jetzt wenden wir die Summenregel an:
P(E) = P(Frauen,Vollzeit) + P(Männer, Vollzeit) = 23,1% + 52,2% = 75,3%
Antwort: 75,3% aller Befragten arbeiten in Vollzeit.