Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/6.Pfadregeln zur Berechnung von Wahrscheinlichkeiten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 31: | Zeile 31: | ||
Ein '''Ereignis''' setzt sich aus mehreren günstigen Ergebnissen zusammen. <br> | Ein '''Ereignis''' setzt sich aus mehreren günstigen Ergebnissen zusammen. <br> | ||
Beispiel:<br> | Beispiel:<br> | ||
Das Ereignis E: Die Münze zeigt mindestens einmal Zahl" setzt sich aus den Ergebnissen (K,Z) und (Z, | Das Ereignis E: Die Münze zeigt mindestens einmal Zahl" setzt sich aus den Ergebnissen (K,Z),(Z,Z)und (Z,K) zusammen. | ||
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse '''addiert'''.<br> | Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse '''addiert'''.<br> | ||
| Zeile 38: | Zeile 38: | ||
Beispiel:<br> | <big>Beispiel:<br> | ||
E: "Die Münze zeigt mindestens einmal Zahl"<br> | E: "Die Münze zeigt mindestens einmal Zahl"<br> | ||
P(E) = P(K,Z) <span style="color:red">'''+'''</span> P(Z,Z)<br> | |||
P(E) = P(K,Z) <span style="color:red">'''+'''</span> P(Z,Z) <span style="color:red">'''+'''</span> P(Z,K)<br> | |||
= <math>\tfrac{1}{4}</math> <span style="color:red"> '''+''' </span> <math>\tfrac{1}{4}</math> <span style="color:red"> '''+''' </span> <math>\tfrac{1}{4}</math> <br> | |||
= <math>\tfrac{3}{4}</math> = 75% | |||
</big> | |||
Baumdiagramm: | Baumdiagramm: | ||
<div class="width-1-2">[[Datei:Baumdiagramm | <div class="width-1-2">[[Datei:Summenregel Baumdiagramm 2.jpg|center]]</div> | ||
<br> | <br> | ||
Falls du noch zusätzliche Hilfe zur Summenregel brauchst benötigst, findest du hier ein Erklärvideo. | Falls du noch zusätzliche Hilfe zur Summenregel brauchst benötigst, findest du hier ein Erklärvideo. | ||
| Zeile 78: | Zeile 80: | ||
b) <math>\tfrac{9}{25}</math> | b) <math>\tfrac{9}{25}</math> | ||
c) <math>\tfrac{ | c) <math>\tfrac{21}{25}</math> | ||
| | | | ||
2= Lösung Übung 1 | | 2= Lösung Übung 1 | | ||
| Zeile 86: | Zeile 88: | ||
{{Box|Übung 2| | {{Box|Übung 2| | ||
Aus einem Behälter mit 8 blauen, 5 roten, 1 schwarze und 5 gelben Kugeln werden | Aus einem Behälter mit 8 blauen, 5 roten, 1 schwarze und 5 gelben Kugeln werden '''<u>gleichzeitig</u>''' zwei Kugeln gezogen. Nach jedem Zug werden die Kugeln wieder zurückgelegt. | ||
Aufgaben: | Aufgaben: | ||
| Zeile 105: | Zeile 107: | ||
|Üben}} | |Üben}} | ||
{{Lösung versteckt| | |||
1= | |||
(5) P(E) = 1 - P(Ē) | |||
Ē: Es wird keine rote und keine gelbe Kugel gezogen. | |||
| | |||
2= Tipp | | |||
3= Verbergen | |||
}} | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 110: | Zeile 125: | ||
b) | b) | ||
(1) <math>\tfrac{ | (1) <math>\tfrac{80}{361}</math> ≈ 22% | ||
(2) <math>\tfrac{ | (2) <math>\tfrac{10}{361}</math> ≈ 3% | ||
(3) <math>\tfrac{ | (3) <math>\tfrac{50}{361}</math> ≈ 14% | ||
(4) <math>\tfrac{240}{361}</math> ≈ 66 | (4) <math>\tfrac{240}{361}</math> ≈ 66% | ||
(5) P(E) = 1 - P(Ē) | (5) P(E) = 1 - P(Ē) | ||
P(E) = 1 - <math>\tfrac{ | P(E) = 1 - <math>\tfrac{80}{361}</math> ≈ 78% | ||
| | | | ||
2= Lösung Übung 2 | | 2= Lösung Übung 2 | | ||
| Zeile 140: | Zeile 155: | ||
(4) <math>\tfrac{11}{36}</math> ≈ 31% | (4) <math>\tfrac{11}{36}</math> ≈ 31% | ||
(5) <math>\tfrac{35}{36}</math> ≈ 97% | (5) <math>\tfrac{35}{36}</math> ≈ 97% | ||
| | |||
2= Lösung Übung 3 | | 2= Lösung Übung 3 | | ||
3= Verbergen | |||
}} | |||
==Mehrstufige Zufallsversuche "ohne zurücklegen"== | |||
Achtung: Bei mehrstufigen Zufallsversuchen ohne zurücklegen, verändert sich die Wahrscheinlichkeit der zweite Stufe. Am Beispiel der Urne kannst du dir das so vorstellen: | |||
In einer Urne sind insgesamt 10 Kugeln. Wird eine Kugel gezogen ohne sie zurückzulegen, hast du im zweiten Zug nur noch insgesamt 9 Kugeln. | |||
{{Box|Übung 4 | | |||
S.190, | |||
Nr.8 b) | |||
Nr.9 | |||
Bei Nr.9 musst du wissen, wie das Kartenspiel aufgebaut ist. | |||
Hier hast du [https://www.skatstube.de/skat-lernen/das-skat-blatt alle Karten] auf einem Blick! Mach davon einen Screenshot und füge diesen in Goodnotes ein! | |||
Noch ein Tipp zu Nr.9: | |||
Zeichne nicht das komplette Baumdiagramm. Überlege dir, welche Pfade für das Ereignis relevant sind! Es reicht, wenn du nur die zeichnest! | |||
|Üben}} | |||
{{Lösung versteckt| | |||
1= | |||
<big>E1: <math>\tfrac{1}{6}</math> ≈ 16,7% | |||
E2: <math>\tfrac{2}{9}</math> ≈ 22,2% | |||
E3: <math>\tfrac{7}{18}</math> ≈ 38,9% | |||
E4: <math>\tfrac{13}{18}</math> ≈ 72,2%</big> | |||
| | |||
2= Lösung Nr.8 | | |||
3= Verbergen | |||
}} | |||
{{Lösung versteckt| | |||
1= | |||
<big>a) <math>\tfrac{7}{124}</math> | |||
b) <math>\tfrac{15}{62}</math> | |||
c) <math>\tfrac{3}{248}</math> | |||
d) <math>\tfrac{33}{248}</math> | |||
e) <math>\tfrac{1}{62}</math> | |||
f) <math>\tfrac{1}{992}</math> </big> | |||
| | |||
2= Lösung Nr.9 | | |||
3= Verbergen | 3= Verbergen | ||
}} | }} | ||
Aktuelle Version vom 19. September 2023, 17:15 Uhr
Wie berechne ich Wahrscheinlichkeiten (mithilfe eines Baumdiagramms)?
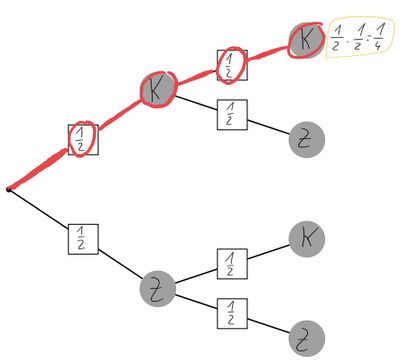
Um zu einem möglichen Ergebnis zu gelangen, musst du einen bestimmten Pfad des Baumdiagrammes gehen. Die Wahrscheinlichkeit dieses Ergebnisses berechnest du, indem du die Wahrscheinlichkeiten entlang des Pfades multiplizierst.
Beispiel:
Es wird eine Münze zweimal geworfen. Mögliche Ergebnisse pro Wurf sind Kopf (K) und Zahl (Z). Die Wahrscheinlichkeit für das Ergebnis Kopf,Kopf lässt sich mit der Produktregel wie folgt berechnen:
P(K,K) = ∙ = = 0,25 = 25%
Baumdiagramm:
Falls du noch zusätzliche Hilfe zur Produktregel brauchst benötigst, findest du hier ein Erklärvideo.
Schaue es nur, wenn du es nicht verstanden hast!!!
Nun betrachten wir nicht mehr nur einzelne Ergebnisse sondern berechnen die Wahrscheinlichkeiten von Ereignissen.
Ein Ereignis setzt sich aus mehreren günstigen Ergebnissen zusammen.
Beispiel:
Das Ereignis E: Die Münze zeigt mindestens einmal Zahl" setzt sich aus den Ergebnissen (K,Z),(Z,Z)und (Z,K) zusammen.
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, werden die einzelnen Wahrscheinlichkeiten der günstigen Ergebnisse addiert.
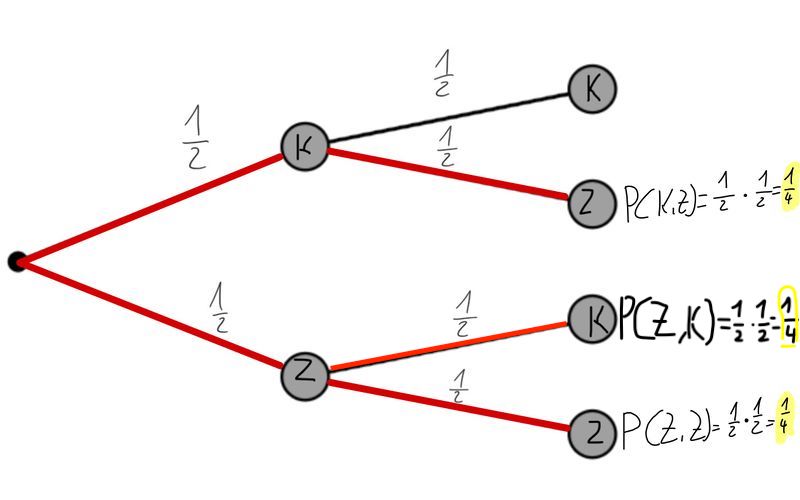
Beispiel:
E: "Die Münze zeigt mindestens einmal Zahl"
P(E) = P(K,Z) + P(Z,Z) + P(Z,K)
= + +
= = 75%
Baumdiagramm:
Falls du noch zusätzliche Hilfe zur Summenregel brauchst benötigst, findest du hier ein Erklärvideo.
Schaue es nur, wenn du es nicht verstanden hast!!!
b)
c)
(5) P(E) = 1 - P(Ē)
Ē: Es wird keine rote und keine gelbe Kugel gezogen.b) (1) ≈ 22% (2) ≈ 3% (3) ≈ 14% (4) ≈ 66% (5) P(E) = 1 - P(Ē)
P(E) = 1 - ≈ 78%
a) Nach jedem Wurf wird notiert, ob eine sechs gefallen ist oder nicht. Die Wahrscheinlichkeit eine sechs zu würfeln beträgt jeweils , keine sechs zu Würfeln
b) (1) ≈ 69% (2) ≈ 28% (3) ≈ 3% (4) ≈ 31%
(5) ≈ 97%
Mehrstufige Zufallsversuche "ohne zurücklegen"
Achtung: Bei mehrstufigen Zufallsversuchen ohne zurücklegen, verändert sich die Wahrscheinlichkeit der zweite Stufe. Am Beispiel der Urne kannst du dir das so vorstellen:
In einer Urne sind insgesamt 10 Kugeln. Wird eine Kugel gezogen ohne sie zurückzulegen, hast du im zweiten Zug nur noch insgesamt 9 Kugeln.
E1: ≈ 16,7% E2: ≈ 22,2% E3: ≈ 38,9%
E4: ≈ 72,2%
a) b) c) d) e)
f)