Benutzer:Gabriel.cicek/Zufällige Ereignisse und ihre Wahrscheinlichkeit/Wahrscheinlichkeit bei mehrstufigen Laplace-Versuchen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{Box|1=Merke|2=<br> Sind bei einem mehrstufigen Zufallsversuch die Wahrscheinlichkeiten auf jeder Stufe gleich groß, so ist der Versuch ein mehrstufiger L…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
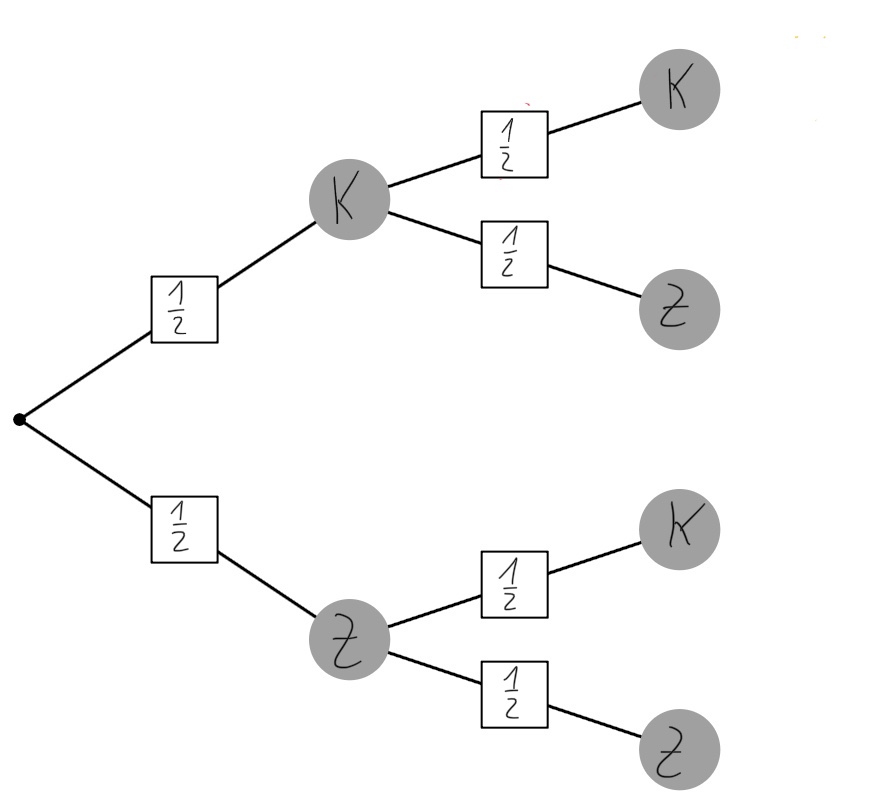
Baumdiagramm und Wahrscheinlichkeiten der Stufen: | Baumdiagramm und Wahrscheinlichkeiten der Stufen: | ||
<div class="width-1-2">[[Datei:Baumdiagramm Münzwurf.jpg| | <div class="width-1-2">[[Datei:Baumdiagramm Münzwurf.jpg|center]]</div> | ||
Wie bei einstufigen Laplace- Zufallsversuchen, ist auch hier die Wahrscheinlichkeit für ein Ereignis: | |||
:<math>P(A) = \frac{\text{Anzahl der günstigen} \text{ Ergebnisse}}{\mathrm{Anzahl\ aller\ m\ddot oglichen\ Ergebnisse}}</math> | |||
Am Beispiel des zweifachen Münzwurfes wäre das für das Ereignis "Nach jedem Wurf zeigt die Münze Zahl": | |||
<big>P(Z,Z) = <math>\tfrac{1}{4} </math>, weil nur ein Ergebnis auf das Ereignis zutrifft und es insgesamt vier Ergebnisse gibt. | |||
<br> | <br> | ||
}} | |||
{{Box|Übung| | |||
Seite 186, | |||
Nr.3-4 | |||
Nr.5 a)-c) | |||
|Üben}} | |||
'''<big>Tipps für die Aufgaben im Buch:</big>''' | |||
'''Aufgabe 4:''' | |||
{{Lösung versteckt| | |||
1= | |||
(1) Differenz ist das Ergebnis eine Subtraktion. Die Differenz von 8 und 3 ist 5. | |||
(2) Die Summe ist das Ergebnis einer Addition. Die Summe von 1 und 3 ist 4. | |||
(4) Das Produkt ist das Ergebnis eine Multiplikation. Das Produkt von 2 und 3 ist 6. | |||
(5) Die Vielfachen von 3 sind 3,6,9,12,15,..., Die Vielfachen von 3 berechnest du, indem du eine ganze Zahl mit 3 multiplizierst. | |||
| | |||
2= Tipp | | |||
3= Verbergen | |||
}} | |||
'''<big>Lösungen für die Aufgaben im Buch:</big>''' | |||
{{Lösung versteckt| | |||
1= | |||
a) Für das Baumdiagramm gibt es keine Lösung. | |||
b) (1) 1/12 | |||
(2) 1/4 | |||
| | |||
2= Lösung Nr.3 | | |||
3= Verbergen | |||
}} | |||
{{Lösung versteckt| | |||
1= | |||
Die Differenz der Augenzahlen ist größer als 2: | |||
Günstige Wurfkombinationen: (6,1);(6,2);(6,3);(5,1);(5,2);(4,1);(1,6);(1,5);(1,4);(2,6);(2,5);(3,6) | |||
Anzahl der günstigen Kombinationen: 12 | |||
Wahrscheinlichkeit: 12/36 = 1/3 | |||
Die Summe der Augenzahlen beträgt 8: | |||
Günstige Wurfkombinationen: (2,6); (3,5); (4,4); (5,3); (6,2) | |||
Anzahl der günstigen Kombinationen: 5 | |||
Wahrscheinlichkeit: 5/36 | |||
Die Summe der Augenzahlen ist kleiner als 5: | |||
Günstige Wurfkombinationen: (1,1); (1,2); (2,1); (1,3); (2,2); (3,1) | |||
Anzahl der günstigen Kombinationen: 6 | |||
Wahrscheinlichkeit: 6/36 = 1/6 | |||
Das Produkt der Augenzahlen beträgt 6: | |||
Günstige Wurfkombinationen: (1,6); (2,3); (3,2); (6,1) | |||
Anzahl der günstigen Kombinationen: 4 | |||
Wahrscheinlichkeit: 4/36 = 1/9 | |||
Die Summe der Augenzahlen ist ein Vielfaches von 3: | |||
Günstige Wurfkombinationen: (3,3); (6,6); (1,2); (2,1); (2,4); (4,2); (3,6); (6,3); (1,5); (5,1); (4,5); (5,4) | |||
Anzahl der günstigen Kombinationen: 12 | |||
Wahrscheinlichkeit: 12/36 = 1/3 | |||
Das Produkt der Augenzahlen ist durch 4 teilbar: | |||
Günstige Wurfkombinationen: (1,4); (2,4); (4,1); (4,2); (2,2); (3,4); (4,3); (2,6); (6,2); (4,4); (4,5); (5,4); (4,6); (6,4); (6,6) | |||
Anzahl der günstigen Kombinationen: 15 | |||
Wahrscheinlichkeit: 15/36 = 5/12 | |||
| | |||
2= Lösung Nr.4 | | |||
3= Verbergen | |||
}} | |||
{{Lösung versteckt| | |||
1= | |||
a) Für das Baumdiagramm gibt es keine Lösung | |||
S = {(RR); (RG); (RS); (GR); (GG); (GS); (SR); (SG); (SS)} | |||
b) 1/9 | |||
c) | |||
P(E1) = 1/3 | |||
P(E2) = 4/9 | |||
P(E3) = 3/9 | |||
P(E4) = 5/9 | |||
| | |||
2= Lösung Nr.5 | | |||
3= Verbergen | |||
}} | }} | ||
Aktuelle Version vom 18. September 2023, 19:18 Uhr
Tipps für die Aufgaben im Buch:
Aufgabe 4:
(1) Differenz ist das Ergebnis eine Subtraktion. Die Differenz von 8 und 3 ist 5.
(2) Die Summe ist das Ergebnis einer Addition. Die Summe von 1 und 3 ist 4.
(4) Das Produkt ist das Ergebnis eine Multiplikation. Das Produkt von 2 und 3 ist 6.
Lösungen für die Aufgaben im Buch:
a) Für das Baumdiagramm gibt es keine Lösung. b) (1) 1/12
(2) 1/4Die Differenz der Augenzahlen ist größer als 2:
Günstige Wurfkombinationen: (6,1);(6,2);(6,3);(5,1);(5,2);(4,1);(1,6);(1,5);(1,4);(2,6);(2,5);(3,6)
Anzahl der günstigen Kombinationen: 12
Wahrscheinlichkeit: 12/36 = 1/3
Die Summe der Augenzahlen beträgt 8:
Günstige Wurfkombinationen: (2,6); (3,5); (4,4); (5,3); (6,2)
Anzahl der günstigen Kombinationen: 5
Wahrscheinlichkeit: 5/36
Die Summe der Augenzahlen ist kleiner als 5:
Günstige Wurfkombinationen: (1,1); (1,2); (2,1); (1,3); (2,2); (3,1)
Anzahl der günstigen Kombinationen: 6
Wahrscheinlichkeit: 6/36 = 1/6
Das Produkt der Augenzahlen beträgt 6:
Günstige Wurfkombinationen: (1,6); (2,3); (3,2); (6,1)
Anzahl der günstigen Kombinationen: 4
Wahrscheinlichkeit: 4/36 = 1/9
Die Summe der Augenzahlen ist ein Vielfaches von 3:
Günstige Wurfkombinationen: (3,3); (6,6); (1,2); (2,1); (2,4); (4,2); (3,6); (6,3); (1,5); (5,1); (4,5); (5,4)
Anzahl der günstigen Kombinationen: 12
Wahrscheinlichkeit: 12/36 = 1/3
Das Produkt der Augenzahlen ist durch 4 teilbar:
Günstige Wurfkombinationen: (1,4); (2,4); (4,1); (4,2); (2,2); (3,4); (4,3); (2,6); (6,2); (4,4); (4,5); (5,4); (4,6); (6,4); (6,6)
Anzahl der günstigen Kombinationen: 15
Wahrscheinlichkeit: 15/36 = 5/12a) Für das Baumdiagramm gibt es keine Lösung
S = {(RR); (RG); (RS); (GR); (GG); (GS); (SR); (SG); (SS)}
b) 1/9
c) P(E1) = 1/3 P(E2) = 4/9 P(E3) = 3/9
P(E4) = 5/9