Benutzer:Meike WWU-12/Entwurf des Lernpfadkapitels: Unfallforensiker*in: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 136: | Zeile 136: | ||
Das Auto im Unfall aus Aufgabe 1 wiegt ca. <math>1,4</math> t und ist nach kurzem Abbremsen vor dem Unfall noch <math>63</math> km/h gefahren. | Das Auto im Unfall aus Aufgabe 1 wiegt ca. <math>1,4</math> t und ist nach kurzem Abbremsen vor dem Unfall noch <math>63</math> km/h gefahren. | ||
'''Bestimme die kinetische Energie beim Aufprall.''' | '''Bestimme die kinetische Energie beim Aufprall und schreibe die Rechnung auf dem Arbeitsblatt auf.''' | ||
{{Lösung versteckt|1= Zunächst müssen alle Werte in die richtigen Einheiten umgerechnet werden. Erinnerung: | {{Lösung versteckt|1= Zunächst müssen alle Werte in die richtigen Einheiten umgerechnet werden. Erinnerung: | ||
| Zeile 145: | Zeile 145: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Als solltest du die Werte umrechnen: | Als erstes solltest du die Werte umrechnen: | ||
Da <math>1</math> t <math>= 1000</math> kg gilt, gilt <math>1,4</math> t<math>= 1400</math> kg. | Da <math>1</math> t <math>= 1000</math> kg gilt, gilt <math>1,4</math> t<math>= 1400</math> kg. | ||
Zudem gilt: | Zudem gilt: | ||
<math>\begin{align} | <math>\begin{align} | ||
63 \frac{km}{h} | 63 \frac{km}{h} &= 63000 \frac{m}{h} \\ | ||
&= 63000 \frac{m}{h} \\ | |||
&= 1050 \frac{m}{min} \\ | &= 1050 \frac{m}{min} \\ | ||
&= 17,5 \frac{m}{s} | &= 17,5 \frac{m}{s} | ||
\end{align}</math>, | \end{align}</math>, | ||
wobei im ersten Schritt durch Multiplikation mit <math>1000</math> km in m umgewandelt wurden und im zweiten und dritten Schritt jeweils durch Division durch <math>60</math> Stunden in Minuten bzw. Minuten in Sekunden umgewandelt wurden. | wobei im ersten Schritt durch Multiplikation mit <math>1000</math> km in m umgewandelt wurden und im zweiten und dritten Schritt jeweils durch Division durch <math>60</math> Stunden in Minuten bzw. Minuten in Sekunden umgewandelt wurden. | ||
| Zeile 160: | Zeile 161: | ||
<math>\begin{align} | <math>\begin{align} | ||
E_{\text{kin}} &= \frac{m \cdot v^2}{2} \\ | E_{\text{kin}} &= \frac{m \cdot v^2}{2} \\ | ||
&= \frac{1400 \cdot 17.5^2}{2} \\ | &= \frac{1400 \cdot 17.5^2}{2} \\ | ||
&= 214.375 [J] \\ | &= 214.375 [J] \\ | ||
| Zeile 188: | Zeile 188: | ||
</gallery> | </gallery> | ||
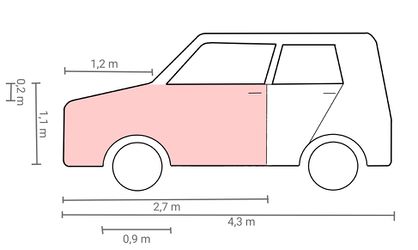
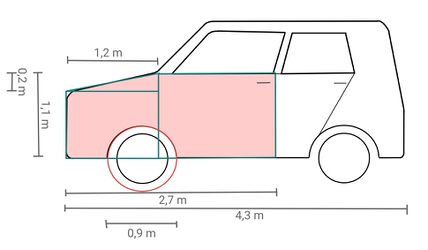
Berechne | '''Berechne, wie groß die beschädigte Fläche, im Bild die rot markierte Fläche, in etwa ist (in m<sup>2</sup>). Runde dabei bei jedem Rechenschritt auf zwei Nachkommastellen und schreibe den Rechenweg auf dem Arbeitsblatt auf.''' | ||
{{Lösung versteckt|1= Um die Fläche | {{Lösung versteckt|1= Um die Fläche ungefähr zu berechnen, kann man die Form des Autos in kleinere Flächen aufteilen und durch Kreise, Dreiecke und Rechtecke annähern. Zum Beispiel so: | ||
<gallery widths="500" heights="250"> | <gallery widths="500" heights="250"> | ||
| Zeile 196: | Zeile 196: | ||
</gallery> | </gallery> | ||
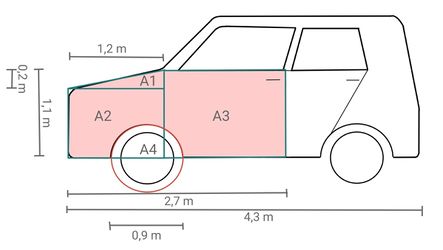
Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten | Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreises) wird abgezogen.|2=Tipp|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 209: | Zeile 209: | ||
<math>\text{A2}</math> ist ein Rechteck mit einer Länge von <math>1.2</math> m und einer Höhe von <math>1.1 \text{m}- 0.2 \text{m} = 0.9 \text{m}</math>, also <math>\text{A2} = 1.2 \cdot 0.9 = 1.08 </math> [m<sup>2</sup>]. | <math>\text{A2}</math> ist ein Rechteck mit einer Länge von <math>1.2</math> m und einer Höhe von <math>1.1 \text{m}- 0.2 \text{m} = 0.9 \text{m}</math>, also <math>\text{A2} = 1.2 \cdot 0.9 = 1.08 </math> [m<sup>2</sup>]. | ||
<math>\text{A3}</math> ist ein Rechteck mit einer Länge von <math>2.7 \text{m} - 1.2 \text{m} = 1.5 \text{m}</math> und einer Höhe von <math>1.1 \text{m}</math>, also <math>\text{A3} = 1.5 \cdot 1.1 = 1.65 </math> [m<sup>2</sup>]. | |||
Fläche <math>\text{A4}</math> ist ein Kreis mit Radius <math>0.9 \text{m}:2 = 0.45 \text{m}</math>, also <math>\text{A4} = \pi \ | Fläche <math>\text{A4}</math> ist ein Kreis mit Radius <math>0.9 \text{m}:2 = 0.45 \text{m}</math>, also <math>\text{A4} = \pi \cdot 0.45^2 \approx 0.64 </math> [m<sup>2</sup>]. | ||
Insgesamt ergibt sich somit für die Fläche A vom Auto: | Insgesamt ergibt sich somit für die Fläche A vom Auto: | ||
<math>\begin{align} | <math>\begin{align} | ||
A &= A1 + A2 + A3 - \frac{A4}{2} \\ | |||
&= 0.12 + 1.08 + 1.65 - 0.32 \\ | &= 0.12 + 1.08 + 1.65 - 0.32 \\ | ||
&= 2.53 | &= 2.53 | ||
\end{align}</math> | \end{align}</math> | ||
Je nachdem, wie du die Fläche angenähert hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. <math>2.53</math> m<sup>2</sup> groß.|2=Lösung|3=Lösung verbergen}} | Je nachdem, wie du die Fläche angenähert hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. <math>2.53</math> m<sup>2</sup> groß.|2=Lösung|3=Lösung verbergen}} | ||
| Zeile 232: | Zeile 232: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
'''Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem Unfall (Schritt 1) und anschließend den Prozentsatz der Reperaturkosten daran und trage alle Werte in die Tabelle ein.''' | '''Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem Unfall (Schritt 1) und anschließend den Prozentsatz der Reperaturkosten daran (Schritt 2) und trage alle Werte in die Tabelle ein. Übertrage nach dem Überprüfen die richtigen Werte auf das Arbeitsblatt.''' | ||
{{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | {{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | ||
| Zeile 242: | Zeile 242: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Wir nutzen die Formel W=p | Wir nutzen die Formel <math>W = p \cot G</math>. | ||
Zu dem '''Restwert''' vor dem Unfall: | Zu dem '''Restwert''' vor dem Unfall: | ||
Es gilt <math>\text{p} =70 | Es gilt <math>\text{p} =70 % =0.7</math>, da der Restwert und nicht der Verlust berechnet werden soll, und <math>\text{G} =21000</math> [€]. | ||
Somit <math>\text{W} =14700</math> [€] | Somit <math>\text{W} =14700</math> [€] | ||
Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | ||
<math>\begin{align} | <math>\begin{align} | ||
\text{W} = \text{p} \cdot \text{G} \Leftrightarrow \text{p} =\ | \text{W} = \text{p} \cdot \text{G} \Leftrightarrow \text{p} = \frac{\text{W}}{\text{G}} | ||
\end{align}</math> | \end{align}</math>. | ||
Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings <math>\text{G} =14700</math> und der Prozentwert ist <math>\text{W} =2500</math>. | Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings <math>\text{G} =14700</math> und der Prozentwert ist <math>\text{W} =2500</math>. | ||
Somit gilt <math>\text{p} \approx 0.17 =17 | Somit gilt <math>\text{p} \approx 0.17 =17 %</math>. | ||
Der Prozentsatz der Reparaturkosten am Restwert des Autos beträgt also ca. <math>17 | Der Prozentsatz der Reparaturkosten am Restwert des Autos beträgt also ca. <math>17 %</math>. | ||
|2=Lösungsweg|3=Lösungsweg verbergen}} | |2=Lösungsweg|3=Lösungsweg verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
Aktuelle Version vom 26. April 2023, 14:19 Uhr
Unfallforensiker:in
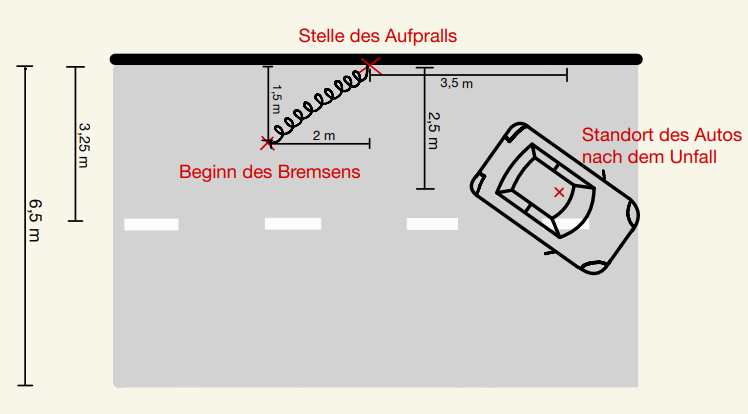
Aufgabe 1: Unfallrekonstruktion
Aufgabe 2: Unfallgutachten