Benutzer:Meike WWU-12/Entwurf des Lernpfadkapitels: Unfallforensiker*in: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (40 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
|1=Info | |1=Info | ||
|2= | |2= | ||
Als Unfallforensiker | Als Unfallforensiker:in kann man arbeiten, wenn man eine Weiterbildung als staatlich geprüfte:r Techniker:in oder Meister:in der Fachrichtung Kraftfahrzeugtechnik oder Maschinenbau oder vergleichbares absolviert und mindestens drei Jahre Berufserfahrung gesammelt hat. Alternativ kann man nach einem abgeschlossenen Studium, zum Beispiel im Bereich Fahrzeugelektronik, in den Beruf einsteigen. Aufgaben sind die Mitarbeit bei der Aufnahme von Verkehrsunfällen, die Sicherung technischer und digitaler Unfallspuren, Vermessung der Unfallstelle, Unfallrekonstruktionen und das Fertigen von Berichten und Stellungnahmen. | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
| Zeile 48: | Zeile 48: | ||
|2=Tipp|3=Tipp verbergen}} | |2=Tipp|3=Tipp verbergen}} | ||
{{Box | Merke | Ein '''spitzer Winkel''' ist | {{Box | Merke | Ein '''spitzer Winkel''' ist größer als <math>0^{\circ}</math> und kleiner als <math>90^{\circ}</math>. Ein '''rechter Winkel''' hat genau <math>90^{\circ}</math>. Ein '''stumpfer Winkel''' ist größer als <math>90^{\circ}</math> und kleiner als <math>180^{\circ}</math>. Einen Winkel von <math>180^{\circ}</math> nennt man '''gestreckten Winkel'''. Ein '''überstumpfer Winkel''' ist größer als <math>180^{\circ}</math> und kleiner als <math>360^{\circ}</math> groß. Ein '''Vollwinkel ''' hat genau <math>360^{\circ}</math>.| Merksatz | Farbe={{Farbe|grün|dunkel}}}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 1b: Unfallrekonstruktion | | {{Box | Aufgabe 1b: Unfallrekonstruktion | | ||
Du | Bei einem Überholmanöver ist ein Auto mit der Fahrbahnbegrenzung des Gegenverkehrs kollidiert. | ||
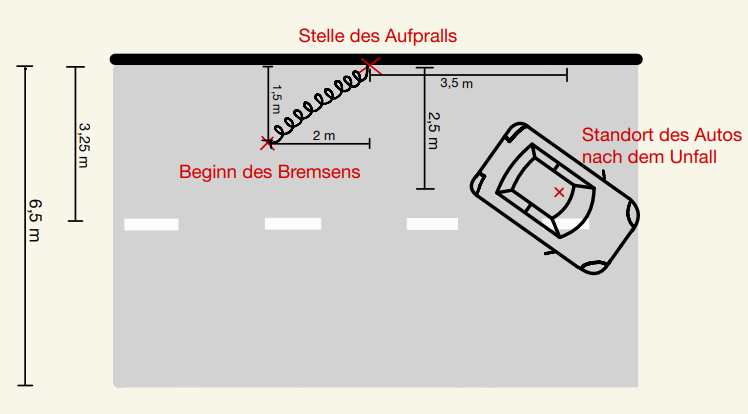
Du stellst als Unfallforensiker:in am Unfallort eine sehr kurze Bremsspur, die Stelle des Aufpralls auf die Fahrbahnbegrenzung sowie die Position des Autos nach dem Unfall fest. Zudem nimmst du einige Messungen vor, sodass folgende Skizze des Unfallortes entsteht: | |||
[[Datei:Unfallstelle.png|800px|middle]] | [[Datei:Unfallstelle.png|800px|middle]] | ||
| Zeile 69: | Zeile 70: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Lösung versteckt|1=Gehe davon aus, dass 2 Kästchen im Koordinatensystem | {{Lösung versteckt|1=Gehe davon aus, dass 2 Kästchen im Koordinatensystem <math>1</math> m in der Realität entsprechen, damit die Skizze maßstabsgetreu ist.|2=Tipp 1|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1=Betrachte die Skizze des Unfallorts und überlege anhand der angegebenen Abmessungen, wie du (1) den Beginn der Bremsspur, (2) den Aufprall des Autos sowie (3) den jetzigen Standort des Autos als drei Punkte im Koordinatensystem darstellen kannst. | {{Lösung versteckt|1=Betrachte die Skizze des Unfallorts und überlege anhand der angegebenen Abmessungen, wie du (1) den Beginn der Bremsspur, (2) den Aufprall des Autos sowie (3) den jetzigen Standort des Autos als drei Punkte im Koordinatensystem darstellen kannst. | ||
Überlege nun, wie du außerdem die Begrenzungen der Straße als Geraden im Koordinatensystem darstellen kannst.|2=Tipp 2|3=Tipp 2 verbergen}} | Überlege nun, wie du außerdem die Begrenzungen der Straße als Geraden im Koordinatensystem darstellen kannst.|2=Tipp 2|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=Als Vereinfachung kannst du annehmen, dass die Bremsspur im Koordinatenursprung beginnt. Zeichne den Beginn des Bremsweges daher als Punkt A(0 | {{Lösung versteckt|1=Als Vereinfachung kannst du annehmen, dass die Bremsspur im Koordinatenursprung beginnt. Zeichne den Beginn des Bremsweges daher als Punkt <math>A(0|0)</math> im Koordinatensystem ein. Aus den gemessenen Entfernungen in der angegebenen Skizze folgt dann, dass das Auto im Punkt <math>B(2|1{,}5)</math> auf die Fahrbahnbegrenzung prallte und schließlich wieder im Punkt <math>C(5{,}5|{-}1)</math> zum Stehen kam. Zeichne diese drei Punkte in das Koordinatensystem ein. Veranschauliche nun die Begrenzungen der Straße, indem du (1) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe <math>1{,}5</math> verläuft, (2) eine Gerade als Mittellinie zeichnest, die parallel zur x-Achse auf Höhe <math>-1{,}75</math> verläuft, und (3) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe <math>-5</math> verläuft. Zuletzt sind noch die Punkte <math>A</math> und <math>B</math> sowie die Punkte <math>B</math> und <math>C</math> jeweils zu verbinden, um den Bremsweg sowie den Weg des Autos nach Aufprall auf die Fahrbahnbegrenzung zu veranschaulichen.|2=Tipp 3|3=Tipp 3 verbergen}} | ||
{{Lösung versteckt|1= Je nachdem, welchen Maßstab du gewählt hast und welche Information der Unfallskizze du als "Ausgangspunkt" der mathematischen SKizze im Koordinatensystem gewählt hast, können sich leicht abweichende | {{Lösung versteckt|1= Je nachdem, welchen Maßstab du gewählt hast und welche Information der Unfallskizze du als "Ausgangspunkt" der mathematischen SKizze im Koordinatensystem gewählt hast, können sich leicht abweichende Darstellungen ergeben. | ||
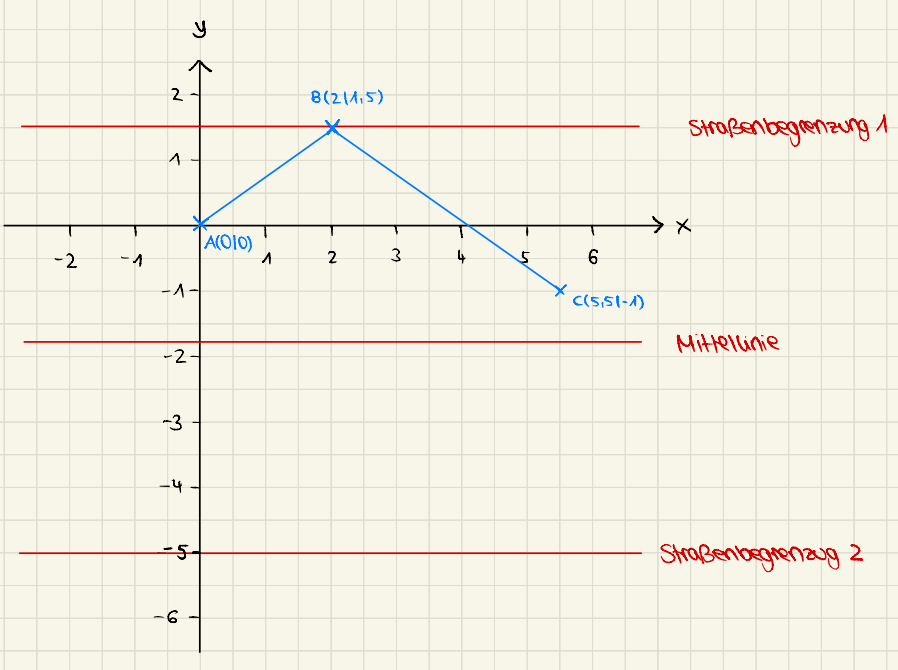
Hier wird angenommen, dass 2 Kästchen in der Realität | Hier wird angenommen, dass 2 Kästchen in der Realität <math>1</math> m entsprechen. Als "Ausgangspunkt" der Skizze wurde der Beginn der Bremsspur als Punkt <math>A(0|0)</math> festgelegt. | ||
[[Datei:Lösung im Koordinatensystem.png|1500px|middle]] | [[Datei:Lösung im Koordinatensystem.png|1500px|middle]] | ||
| Zeile 95: | Zeile 96: | ||
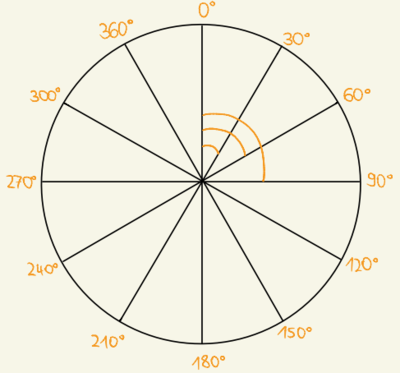
Du hast nun als Unfallforensiker:in die Aufgabe, den Einlauf- bzw. Auslaufwinkel in der vorliegenden Unfallsituation zu bestimmen. | Du hast nun als Unfallforensiker:in die Aufgabe, den Einlauf- bzw. Auslaufwinkel in der vorliegenden Unfallsituation zu bestimmen. | ||
'''Miss dazu im Koordinatensystem, das in | '''Miss dazu im Koordinatensystem, das in Aufgabe 1b angefertigt wurde, den Einlauf- bzw. Auslaufwinkel mithilfe eines Geodreiecks. Trage den gemessenen Winkel an passender Stelle in das Koordinatensystem aus Aufgabe 1b ein.''' | ||
| Zeile 103: | Zeile 104: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Lösung versteckt|1=Falls du in Aufgabe 1b keine geeignete Skizze im Koordinatensystem anfertigen konntest, mache einen Screenshot von der zur Verfügung gestellten Lösung zu Aufgabe 1b. Füge | {{Lösung versteckt|1=Falls du in Aufgabe 1b keine geeignete Skizze im Koordinatensystem anfertigen konntest, mache einen Screenshot von der zur Verfügung gestellten Lösung zu Aufgabe 1b. Füge dieses dann auf deinem Arbeitsblatt ein und miss dort den geforderten Winkel.|2=Tipp 1|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1=Falls du nicht mehr weißt, wie man mit dem Geodreieck Winkel misst: | {{Lösung versteckt|1=Falls du nicht mehr weißt, wie man mit dem Geodreieck Winkel misst: | ||
| Zeile 110: | Zeile 111: | ||
{{Lösung versteckt|1= Es gilt Einlaufwinkel=Auslaufwinkel. Daher reicht es, einen der beiden Winkel zu messen. | {{Lösung versteckt|1= Es gilt Einlaufwinkel=Auslaufwinkel. Daher reicht es, einen der beiden Winkel zu messen. | ||
Es ergibt sich '''Einlaufwinkel= | Es ergibt sich '''Einlaufwinkel=Auslaufwinkel≈<math>36^{\circ}</math>'''. | ||
|2=Lösung|3=Lösung verbergen}} | |2=Lösung|3=Lösung verbergen}} | ||
| Zeile 132: | Zeile 133: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Box | 1=Merksatz: Formel für die kinetische Energie | 2=Die kinetische Energie bestimmt man mit der Formel | {{Box | 1=Merksatz: Formel für die kinetische Energie | 2=Die kinetische Energie bestimmt man mit der Formel <math>E_{\text{kin}} = \frac{m \cdot v^2}{2}</math>, wobei die kinetische Energie <math>E_{\text{kin}}</math> in Joule angegeben wird, die Masse <math>m</math> in kg und die Geschwindigkeit <math>v</math> in s. Es gilt außerdem <math>1 J= 1\cdot \frac{kg \cdot m^2}{s^2}</math>.| 3=Merksatz |Farbe={{Farbe|grün|dunkel}}}} | ||
Das Auto im Unfall aus Aufgabe | Das Auto im Unfall aus Aufgabe 1 wiegt ca. <math>1,4</math> t und ist nach kurzem Abbremsen vor dem Unfall noch <math>63</math> km/h gefahren. | ||
'''Bestimme die kinetische Energie beim Aufprall und schreibe die Rechnung auf dem Arbeitsblatt auf.''' | |||
{{Lösung versteckt|1= Zunächst müssen alle Werte in die richtigen Einheiten umgerechnet werden. Erinnerung: | |||
<math>1</math> t <math>= 1000</math> kg. | |||
Um km/h in m/s umzurechnen, multiplizierst du am besten erst mit <math>1000</math>, dann erhältst du einen Wert in m/h und dividierst dann durch <math>3600</math> bzw. zweimal durch <math>60</math>, denn eine Stunde sind <math>3600</math> Sekunden. | |||
|2=Tipp|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= | |||
Als erstes solltest du die Werte umrechnen: | |||
Da <math>1</math> t <math>= 1000</math> kg gilt, gilt <math>1,4</math> t<math>= 1400</math> kg. | |||
Zudem gilt: | |||
<math>\begin{align} | |||
63 \frac{km}{h} &= 63000 \frac{m}{h} \\ | |||
&= 1050 \frac{m}{min} \\ | |||
&= 17,5 \frac{m}{s} | |||
\end{align}</math>, | |||
wobei im ersten Schritt durch Multiplikation mit <math>1000</math> km in m umgewandelt wurden und im zweiten und dritten Schritt jeweils durch Division durch <math>60</math> Stunden in Minuten bzw. Minuten in Sekunden umgewandelt wurden. | |||
Durch Einsetzen der Werte in die Lösung ergibt sich: | |||
<math>\begin{align} | |||
E_{\text{kin}} &= \frac{m \cdot v^2}{2} \\ | |||
&= \frac{1400 \cdot 17.5^2}{2} \\ | |||
&= 214.375 [J] \\ | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe=#CD2990 }} | | Arbeitsmethode | Farbe=#CD2990 }} | ||
| Zeile 145: | Zeile 175: | ||
'''Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts A zu. Überprüfe deine Lösung.''' | '''Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts <math>A</math> zu. Überprüfe deine Lösung.''' | ||
{{LearningApp|width=100%|height=500px|app=pnf5uwamn23}} | {{LearningApp|width=100%|height=500px|app=pnf5uwamn23}} | ||
| Zeile 158: | Zeile 188: | ||
</gallery> | </gallery> | ||
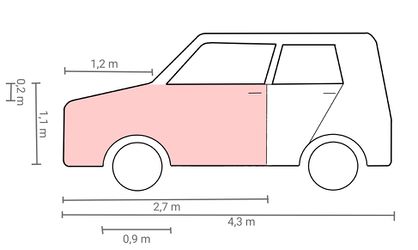
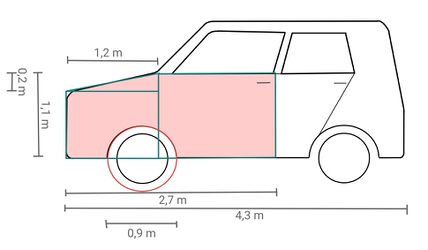
Berechne | '''Berechne, wie groß die beschädigte Fläche, im Bild die rot markierte Fläche, in etwa ist (in m<sup>2</sup>). Runde dabei bei jedem Rechenschritt auf zwei Nachkommastellen und schreibe den Rechenweg auf dem Arbeitsblatt auf.''' | ||
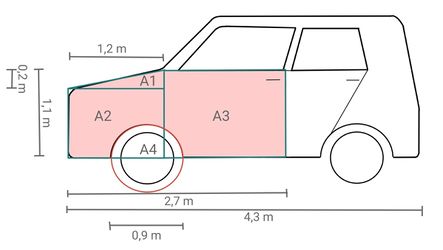
{{Lösung versteckt|1= Um die Fläche | {{Lösung versteckt|1= Um die Fläche ungefähr zu berechnen, kann man die Form des Autos in kleinere Flächen aufteilen und durch Kreise, Dreiecke und Rechtecke annähern. Zum Beispiel so: | ||
<gallery widths="500" heights="250"> | <gallery widths="500" heights="250"> | ||
| Zeile 166: | Zeile 196: | ||
</gallery> | </gallery> | ||
Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten | Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreises) wird abgezogen.|2=Tipp|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= | |||
Wir berechnen mit der im Tipp gegebenen Einteilung: | |||
<gallery widths="500" heights="250"> | |||
Datei:Flächeninhalt Auto mit Markierung.jpg | |||
</gallery> | |||
Dann gilt: <math>\text{A1}</math> ist ein rechtwinkliges Dreieck mit einer Höhe von <math>0.2 \text{m}</math>und einer Grundseite der Länge <math>1.2 \text{m}</math>, somit <math>\text{A1} = \frac{1.2 \cdot 0.2}{2} = 0.12</math> [m<sup>2</sup>] | |||
<math>\text{A2}</math> ist ein Rechteck mit einer Länge von <math>1.2</math> m und einer Höhe von <math>1.1 \text{m}- 0.2 \text{m} = 0.9 \text{m}</math>, also <math>\text{A2} = 1.2 \cdot 0.9 = 1.08 </math> [m<sup>2</sup>]. | |||
<math>\text{A3}</math> ist ein Rechteck mit einer Länge von <math>2.7 \text{m} - 1.2 \text{m} = 1.5 \text{m}</math> und einer Höhe von <math>1.1 \text{m}</math>, also <math>\text{A3} = 1.5 \cdot 1.1 = 1.65 </math> [m<sup>2</sup>]. | |||
Fläche <math>\text{A4}</math> ist ein Kreis mit Radius <math>0.9 \text{m}:2 = 0.45 \text{m}</math>, also <math>\text{A4} = \pi \cdot 0.45^2 \approx 0.64 </math> [m<sup>2</sup>]. | |||
Insgesamt ergibt sich somit für die Fläche A vom Auto: | |||
<math>\begin{align} | |||
A &= A1 + A2 + A3 - \frac{A4}{2} \\ | |||
&= 0.12 + 1.08 + 1.65 - 0.32 \\ | |||
&= 2.53 | |||
\end{align}</math> | |||
Je nachdem, wie du die Fläche angenähert hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. <math>2.53</math> m<sup>2</sup> groß.|2=Lösung|3=Lösung verbergen}} | |||
|Arbeitsmethode | Farbe={{Farbe|orange}} }} | |Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 2d⭐: Schadensbegutachtung | | {{Box | Aufgabe 2d⭐: Schadensbegutachtung | | ||
Nach Absprache mit einer Werkstatt erfährst du, dass die Reparaturkosten 2.500 € betragen. Das Auto hat ursprünglich 21.000 € gekostet und hatte durch den alltäglichen Verschleiß und das Alter vor dem Unfall bereits einen Werteverlust von 30%. | Nach Absprache mit einer Werkstatt erfährst du, dass die Reparaturkosten <math>2.500</math> € betragen. Das Auto hat ursprünglich <math>21.000</math> € gekostet und hatte durch den alltäglichen Verschleiß und das Alter vor dem Unfall bereits einen Werteverlust von 30%. | ||
{{Box | {{Box | ||
| Zeile 180: | Zeile 232: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem | '''Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem Unfall (Schritt 1) und anschließend den Prozentsatz der Reperaturkosten daran (Schritt 2) und trage alle Werte in die Tabelle ein. Übertrage nach dem Überprüfen die richtigen Werte auf das Arbeitsblatt.''' | ||
{{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | {{LearningApp|width=100%|height=500px|app=pgqvqcz9j23}} | ||
{{Lösung versteckt|1=Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein | {{Lösung versteckt|1=Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein <math>W=p \cdot G</math>, wobei <math>W</math> der '''Prozentwert''', <math>p</math> der '''Prozentsatz''' und <math>G</math> der '''Grundwert''' ist. | ||
Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und 100%-30%=70%) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll. | Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und <math>100% - 30% = 70%</math>) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll. | ||
Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.|2=Tipp|3=Tipp verbergen}} | Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.|2=Tipp|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Wir nutzen die Formel W=p | Wir nutzen die Formel <math>W = p \cot G</math>. | ||
Zu dem '''Restwert''' vor dem Unfall: | Zu dem '''Restwert''' vor dem Unfall: | ||
Es gilt p=70%=0 | Es gilt <math>\text{p} =70 % =0.7</math>, da der Restwert und nicht der Verlust berechnet werden soll, und <math>\text{G} =21000</math> [€]. | ||
Somit W=14700 [€] | Somit <math>\text{W} =14700</math> [€] | ||
Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | Zum '''Prozentsatz''' der Reparaturkosten am Restwert: | ||
<math>\begin{align} | <math>\begin{align} | ||
W | \text{W} = \text{p} \cdot \text{G} \Leftrightarrow \text{p} = \frac{\text{W}}{\text{G}} | ||
\end{align}</math> | \end{align}</math>. | ||
Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings G=14700 und der Prozentwert ist W=2500. | |||
Somit gilt | Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings <math>\text{G} =14700</math> und der Prozentwert ist <math>\text{W} =2500</math>. | ||
Somit gilt <math>\text{p} \approx 0.17 =17 %</math>. | |||
Der | Der Prozentsatz der Reparaturkosten am Restwert des Autos beträgt also ca. <math>17 %</math>. | ||
|2=Lösungsweg|3=Lösungsweg verbergen}} | |2=Lösungsweg|3=Lösungsweg verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
| Zeile 210: | Zeile 263: | ||
{{Box | Aufgabe 2e⭐: Geschwindigkeit berechnen | | {{Box | Aufgabe 2e⭐: Geschwindigkeit berechnen | | ||
[[Datei:Unfallort Bremsweg.png|mini]] | [[Datei:Unfallort Bremsweg.png|mini]] | ||
Am Unfallort ist aufgefallen, dass ein zweites | Am Unfallort ist aufgefallen, dass ein zweites Fahrzeug nur knapp vor dem verunfallten Wagen zum Stehen kam. | ||
Im Rahmen der Unfallanalyse untersuchst du als Unfallforensiker:in, ob sich die fahrende Person im zweiten Auto an die vorgeschriebene | Im Rahmen der Unfallanalyse untersuchst du als Unfallforensiker:in, ob sich die fahrende Person im zweiten Auto an die vorgeschriebene Geschwindigkeitsbegrenzung gehalten hat. Um dies herauszufinden, wird die Länge der entstandenen Bremsspur gemessen. So kann mit wenigen Schritten ermittelt werden, wie hoch die Geschwindigkeit vor dem Unfall war. | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=Die Länge des Bremsweges | |2=Die Länge des Bremsweges in m bestimmt man mit der Formel <math>b(x) = \frac{x^2}{100}</math>, wobei <math>x</math> die Geschwindigkeit in km/h angibt. | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
Es ist eine Bremsspur mit einer Länge von <math>49</math> m entstanden. | |||
'''Berechne, wie hoch die Geschwindigkeit des zweiten Autos war.''' | |||
'''Kreuze auf dem Arbeitsblatt an, ob sich die fahrende Person an die vorgeschriebene Geschwindigkeitsbegrenzung von <math>50</math> km/h gehalten hat.''' | |||
{{Lösung versteckt|1=Nutze Äquivalenzumformungen! Du weißt, dass der Bremsweg <math>49</math> m betrug. Löse die Gleichung <math>49 = \frac{x^2}{100}</math> nach <math>x</math> auf, um die Geschwindigkeit zu bestimmen.|2=Tipp 1|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Multipliziere zunächst beide Seiten der Gleichung mit <math>100</math>.|2=Tipp 2|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1=Ziehe schließlich auf beiden Seiten der Gleichung die Wurzel. Entscheide, welches Ergebnis im Sachzusammenhang geeignet ist.|2=Tipp 3|3=Tipp 3 verbergen}} | |||
{{Lösung versteckt|1= | |||
<math>\begin{align} | |||
& & b(x) &= \frac{x^2}{100} & &\mid \text{Einsetzen}\\ | |||
\Leftrightarrow & & 49 &= \frac{x^2}{100} & &\mid \cdot 100\\ | |||
\Leftrightarrow & & 49 \cdot 100 &= x^2 & &\mid \surd\\ | |||
\Leftrightarrow & & \pm \sqrt{4900} &= x & &\mid \text{Berechnen}\\ | |||
\Leftrightarrow & & \pm 70 &= x | |||
\end{align}</math> | |||
Da es keine negativen Geschwindigkeiten gibt, eignet sich im Sachzusammenhang nur die Lösung <math>x = 70</math>. Somit ist aus der Bremsspur von <math>49</math> m auf eine Geschwindigkeit des zweiten Autos von <math>70</math> km/h zu schließen. Die fahrende Person hat sich also nicht an die vorgegebene Geschwindigkeitsbegrenzung von <math>50</math> km/h gehalten. | |||
|2=Lösung|3=Lösung verbergen}} | |||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
Aktuelle Version vom 26. April 2023, 14:19 Uhr
Unfallforensiker:in
Aufgabe 1: Unfallrekonstruktion
Aufgabe 2: Unfallgutachten