Anton-Philipp-Reclam-Gymnasium Leipzig/Kraefte723/Kräfte an der Schraubenfeder: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Beispiel Schraubenfeder Diagramm.jpg|alternativtext=Beispiel Schraubenfeder Diagramm|mini]] | |||
==Kräfte an der Schraubenfeder== | |||
[[Datei:Kräfte an der Schraubenfeder.lol.png|alternativtext=Kräfte an der Schraubenfeder|mini]] | [[Datei:Kräfte an der Schraubenfeder.lol.png|alternativtext=Kräfte an der Schraubenfeder|mini]] | ||
[[Datei:Unterschied Kräfte an der Schraubenfeder.png|alternativtext=Unterschied Kräfte an der Schraubenfeder|mini]] | [[Datei:Unterschied Kräfte an der Schraubenfeder.png|alternativtext=Unterschied Kräfte an der Schraubenfeder|mini]] | ||
| Zeile 4: | Zeile 8: | ||
Die Verlängerung einer Schraubenfeder ist proportional zur wirkenden Kraft: F~s. | Die Verlängerung einer Schraubenfeder ist proportional zur wirkenden Kraft: F~s. | ||
====1. Berechnung==== | |||
Man berechnet es mit: F = D•s. D = Federkonstante und s = cm. | Man berechnet es mit: F = D•s. D = Federkonstante und s = cm. | ||
Beispiel: | ====2. Beispiel==== | ||
[[:Datei:Beispiel Schraubenfeder Diagramm.jpg|Beispiel]]: | |||
F | F | ||
| Zeile 22: | Zeile 30: | ||
0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 | ||
====3. Kleiner Text==== | |||
Wenn man die Verlängerung der Schraubenfeder verdoppelt, | Wenn man die Verlängerung der Schraubenfeder verdoppelt, | ||
| Zeile 29: | Zeile 38: | ||
dass für viele elastische Körper das folgende Gesetz gilt: | dass für viele elastische Körper das folgende Gesetz gilt: | ||
F = D•s | F = D•s | ||
====4. Lückentext==== | |||
<br /> | <br /> | ||
| Zeile 37: | Zeile 48: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
In diesem Lückentext geht es um die …………………………… . Wenn man die Kraft verdoppelt, so <u>………………</u> sich auch die Verlängerung der Schraubenfeder. Dann hat der englische Wissenschaftler <u>………….</u> erkannt, | In diesem Lückentext geht es um die <u>…………………………… .</u> . Wenn man die Kraft verdoppelt, so <u>………………</u> sich auch die Verlängerung der Schraubenfeder. Dann hat der englische Wissenschaftler <u>………….</u> erkannt, | ||
dass für viele elastische Körper das folgende <u>…………………</u> gilt. | dass für viele elastische Körper das folgende <u>…………………</u> gilt. | ||
Man berechnet: <u>………………………………………………………………</u> . | Man berechnet: <u>………………………………………………………………</u> . | ||
Aktuelle Version vom 25. Januar 2023, 10:07 Uhr
Kräfte an der Schraubenfeder
Ebenso gibt es auch die Kräfte an der Schraubenfeder.
Die Verlängerung einer Schraubenfeder ist proportional zur wirkenden Kraft: F~s.
1. Berechnung
Man berechnet es mit: F = D•s. D = Federkonstante und s = cm.
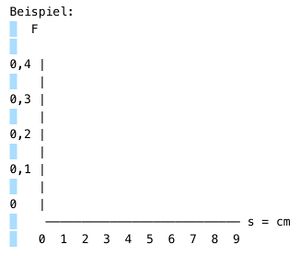
2. Beispiel
F
0,4 |
|
0,3 |
|
0,2 |
|
0,1 |
|
0 |
——————————————————————————— s = cm 0 1 2 3 4 5 6 7 8 9
3. Kleiner Text
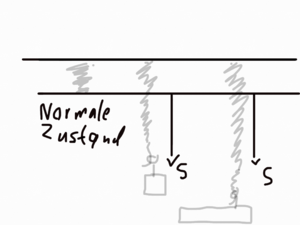
Wenn man die Verlängerung der Schraubenfeder verdoppelt, verdoppelt sich auch die Kraft. Und eine Verdreifachung der Kraft bewirkt seine Verdreifachung der Verlängerung. Nähmlich der englische Wissenschaftler Robert Hooke (1635-1703) hat herausgefunden, dass für viele elastische Körper das folgende Gesetz gilt: F = D•s
4. Lückentext
Und jetzt ein Lückentext für euch!!!
In diesem Lückentext geht es um die …………………………… . . Wenn man die Kraft verdoppelt, so ……………… sich auch die Verlängerung der Schraubenfeder. Dann hat der englische Wissenschaftler …………. erkannt, dass für viele elastische Körper das folgende ………………… gilt. Man berechnet: ……………………………………………………………… .