Anton-Philipp-Reclam-Gymnasium Leipzig/Kraefte744/Reibungskräfte: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (31 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Reibungskraft | ==='''<u>Reibungskraft</u>'''=== | ||
====<u>Definition</u>==== | |||
Die Reibungskraft ist eine Kraft, die zwischen den Oberflächen von zwei sich berührenden Körpern wirkt. Reibung entsteht dann, wenn zwei Körper aufeinander liegen, gleiten oder rollen. | |||
Unter dem Mikroskop erkennt man dass Oberflächen nie komplett glatt sind >> Körper verhaken sich. Je rauer die Oberfläche ist, desto mehr Kraftaufwand wird benötigt. | |||
Reibungskraft wirkt entgegen der Bewegung. | |||
Formelzeichen: F | '''Formelzeichen:''' F | ||
Einheit: N (Newton) oder J (Joule) | '''Einheit:''' N (Newton) oder J (Joule) | ||
Messgerät: Federkraftmesser | '''Messgerät''': Federkraftmesser | ||
<br /> | |||
=====Reibungskraftarten===== | |||
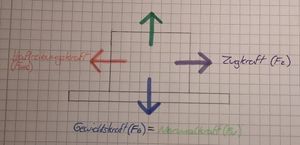
[[Datei:Skizze zur Haftreibungskraft.jpg|mini|Holzklotz auf ebenen Holzboden(Haftreibungskraft)]] | |||
'''Haftreibungskraft(F<sub>HR</sub>):''' | |||
- Kraft wirkt zwischen zwei zueinander ruhenden Körpern | |||
- Zugkraft (F<sub>Z</sub>) </= Haftreibungskraft (F<sub>HR</sub>) | |||
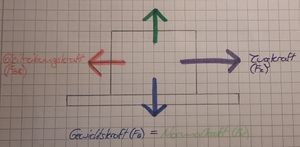
Gleitreibungskraft(F | '''Gleitreibungskraft(F<sub>GR</sub>):''' | ||
- Kraft wirkt zwischen zwei zueinander bewegten Körpern[[Datei:Skizze Gleitreibungskraft.jpg|mini|Holzklotz auf ebenen Holzboden(Gleitreibungskraft)]]- Zugkraft (F<sub>Z</sub>) > Gleitreibungskraft (F<sub>GR</sub>) | |||
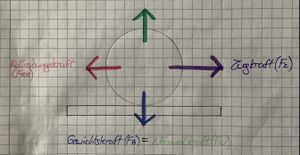
Rollreibungskraft(F | '''Rollreibungskraft(F<sub>RR</sub>):''' | ||
- Kraft wirkt beim Abrollen eines Wälzkörpers | |||
- Zugkraft (F<sub>Z</sub>) > Rollreibungskraft (F<sub>RR</sub>) | |||
<u>'''''MERKE:'''''</u> | |||
[[Datei:Eine Skizze zur Rollreibung.jpg|mini|Holzrad auf ebenen Holzboden(Rollreibungskraft)]] | |||
Ruhestand = Haftreibungskraft | Ruhestand = Haftreibungskraft | ||
| Zeile 39: | Zeile 44: | ||
Wälzbewegung = Rollreibungskraft | Wälzbewegung = Rollreibungskraft | ||
====<u>Berechnung</u> ==== | |||
F<sub>R</sub>= µ x F<sub>N</sub> (Reibungskraft = Reibungskoeffizient x Normalkraft) | |||
=====Beispielaufgabe===== | |||
Tim zieht ein 20kg schweres Aluminiumkomplettrad über eine ebene trockene asphaltierte Straße. | |||
'''1.''' Wie hoch ist die Haftreibungskraft? | |||
'''2.''' Wie viel Kraft muss er anwenden, um das Rad zum Rutschen/Gleiten zubekommen? | |||
'''3.''' Wie viel Kraft braucht man um das Rad zum Rollen zu bringen? | |||
'''Ges.:''' Kraft in N | |||
'''Geg.:''' | |||
- Ebene Fläche | |||
- Reifen auf trockenen Asphalt ( µ<sub>HR</sub> = 0,8 / µ<sub>GR</sub> = 0,5 / µ<sub>RR</sub> = 0,02 ) [Koeffizient bei ebener Fläche im Formelsammlung Seite 76.] | |||
F<sub>G</sub> = M x 10 = 20 kg x 10 = 200N | |||
200N ( F<sub>G</sub>) = 200N (F<sub>N</sub>) | |||
Lösung: | |||
#F<sub>HR</sub> = µ<sub>H</sub> x F<sub>N</sub> = 0,8 x 200 N = '''160 N''' | |||
#F<sub>GR</sub> = µ<sub>GR</sub> x F<sub>N</sub> = 0,5 x 200 N = '''100 N''' | |||
#F<sub>RR</sub> = µ<sub>RR</sub> x F<sub>N</sub> = 0,02 x 200 N = '''4 N''' | |||
<br /> | |||
====<u>Übungsaufgaben</u>==== | |||
'''1.'''Ein Stapel Stahlplatten liegt auf dem Tisch. | |||
Eine Stahlplatte wiegt 500g. Wie hoch ist die ist Haftreibungskraft, wenn der Stapel aus 12 Platten besteht? | |||
'''2.'''Die Haftreibungskraft einer Holzhütte auf Holzgrund ist 1.980 N (Newton). | |||
Wieviel wiegt die Holzhütte? Wie viel Kraft brauche ich um sie in Bewegung zu halten / weiter zu schieben? | |||
'''Zusatz:''' | |||
Was bewirkt ein Spanngurt bei der Palette auf der Ladefläche eines LKWs ? | |||
=====Lösung===== | |||
'''1.''' | |||
'''ges.:''' Haftreibungskraft (N) | |||
'''geg.:''' M (Masse) = 500g x 12 | |||
Reibungszahl Stahl auf Holz (µ) = 0,6 | |||
'''Lösung:''' | |||
500g x 12 = 6000g = 6 kg | |||
F<sub>G</sub>= 6kg x 10 = 60 N | |||
F<sub>N</sub>= 60 N | |||
F<sub>HR</sub>= µ<sub>HR</sub> x F<sub>N</sub> = 0,6 x 60 N = 36 N | |||
'''2.''' | |||
'''ges.:''' M (Masse) in kg, | |||
F<sub>GR</sub> (N) | |||
'''geg.:''' F<sub>HR</sub> = 1980 N | |||
'''Lösung:''' | |||
I.) | |||
F<sub>G</sub> = µ x F<sub>N</sub> I /µ | |||
F<sub>G</sub> / µ = F<sub>N</sub> =1980 N / 0,6 = 3300N | |||
F<sub>N</sub> = M x10 I / 10 | |||
F<sub>N</sub> / 10 = M = 3300N / 10 = 330 Kg | |||
II.) | |||
F<sub>GR</sub> = µ<sub>GR</sub> x F<sub>N</sub> = 0,35 x 3300 N = 1155 N | |||
'''Antwort:''' Um die 330kg schwere Holzhütte in Bewegung zu halten benötigt man 1155 N. | |||
'''Zusatz:''' Das Spanngurt erhöht den Anpressdruck der Palette auf der Ladefläche und erhöht damit die Haftreibungskraft zwischen der Palette und der Ladefläche. | |||
====<u>Schülerexperiment</u>==== | |||
=====Material===== | |||
- Federkraftmesser (Fz<sub>max</sub> = 3 N ) | |||
- Holzklotz ( F<sub>G</sub> = 30 g = F<sub>N</sub> = 0,30 N) | |||
- halbvolle Duftsanddose ( F<sub>G</sub>= 455 g = F<sub>N</sub> = 4,55 N ) | |||
- Holzbalken (geschliffen, unlackiert) | |||
=====Verlauf===== | |||
- Duftsand auf Holklotz stellen = F<sub>N</sub> = 0,30N + 4,55 N = <u>4,85 N)</u>[[Datei:Physik Kraftreibung von der Seite.mp4|mini|Holzklotz über Holzbalken von der Seite]] | |||
- gleichmäßig mit Federkraftmesser (F<sub>Z</sub>) über Holzbalken ziehen = F<sub>GR</sub>[[Datei:Physik Kraftreibung von oben.mp4|mini|Holzklotz über Holzbalken von oben]] | |||
<br /> | |||
=====Beobachtung===== | |||
- bleibt bis Fz 1,45 N haften = F<sub>HR</sub> | |||
- sobald es gleitet sinkt die Fz auf 1,30 N = F<sub>GR</sub> | |||
<br /> | |||
=====Berechnung===== | |||
'''ges:''' Reibungkoeffizient (µ<sub>HR</sub> / µ<sub>GR</sub>) | |||
'''geg:''' F<sub>HR</sub> = 1,45 N | |||
F<sub>GR</sub> = 1,30 N | |||
F<sub>N</sub> = 4,85 N | |||
'''Lösung:''' | |||
F<sub>HR</sub> = µ<sub>HR</sub> x F<sub>N</sub> <big>I</big> :F<sub>N</sub> | |||
F<sub>HR</sub> / F<sub>N</sub> = µ<sub>HR</sub> | |||
1,45 N / 4,85 = <u>0,30</u> | |||
F<sub>GR</sub> = µ<sub>GR</sub> x F<sub>N</sub> <big>I</big> :F<sub>N</sub> | |||
F<sub>GR</sub> / F<sub>N</sub> = µ<sub>GR</sub> | |||
1,30 N / 4,85 N = <u>0,27</u> | |||
'''Antwort:''' Bei einem geschliffenen, unlackiertem Holzuntergrund beträgt der Haftreibungskoeffizient 0,30 und der Gleitreibungskoeffizient 0,27.<br /> | |||
<br /> | |||
=== Quellen === | |||
- Wissen: studyflix.de, Formelsammlung | |||
- Video + Bilder: Eigenproduktion | |||
Aktuelle Version vom 15. Januar 2023, 12:37 Uhr
Reibungskraft
Definition
Die Reibungskraft ist eine Kraft, die zwischen den Oberflächen von zwei sich berührenden Körpern wirkt. Reibung entsteht dann, wenn zwei Körper aufeinander liegen, gleiten oder rollen.
Unter dem Mikroskop erkennt man dass Oberflächen nie komplett glatt sind >> Körper verhaken sich. Je rauer die Oberfläche ist, desto mehr Kraftaufwand wird benötigt.
Reibungskraft wirkt entgegen der Bewegung.
Formelzeichen: F
Einheit: N (Newton) oder J (Joule)
Messgerät: Federkraftmesser
Reibungskraftarten
Haftreibungskraft(FHR):
- Kraft wirkt zwischen zwei zueinander ruhenden Körpern
- Zugkraft (FZ) </= Haftreibungskraft (FHR)
Gleitreibungskraft(FGR):
- Kraft wirkt zwischen zwei zueinander bewegten Körpern
- Zugkraft (FZ) > Gleitreibungskraft (FGR)
Rollreibungskraft(FRR):
- Kraft wirkt beim Abrollen eines Wälzkörpers
- Zugkraft (FZ) > Rollreibungskraft (FRR)
MERKE:
Ruhestand = Haftreibungskraft
Bewegung = Gleitreibungskraft
Wälzbewegung = Rollreibungskraft
Berechnung
FR= µ x FN (Reibungskraft = Reibungskoeffizient x Normalkraft)
Beispielaufgabe
Tim zieht ein 20kg schweres Aluminiumkomplettrad über eine ebene trockene asphaltierte Straße.
1. Wie hoch ist die Haftreibungskraft?
2. Wie viel Kraft muss er anwenden, um das Rad zum Rutschen/Gleiten zubekommen?
3. Wie viel Kraft braucht man um das Rad zum Rollen zu bringen?
Ges.: Kraft in N
Geg.:
- Ebene Fläche
- Reifen auf trockenen Asphalt ( µHR = 0,8 / µGR = 0,5 / µRR = 0,02 ) [Koeffizient bei ebener Fläche im Formelsammlung Seite 76.]
FG = M x 10 = 20 kg x 10 = 200N
200N ( FG) = 200N (FN)
Lösung:
- FHR = µH x FN = 0,8 x 200 N = 160 N
- FGR = µGR x FN = 0,5 x 200 N = 100 N
- FRR = µRR x FN = 0,02 x 200 N = 4 N
Übungsaufgaben
1.Ein Stapel Stahlplatten liegt auf dem Tisch.
Eine Stahlplatte wiegt 500g. Wie hoch ist die ist Haftreibungskraft, wenn der Stapel aus 12 Platten besteht?
2.Die Haftreibungskraft einer Holzhütte auf Holzgrund ist 1.980 N (Newton).
Wieviel wiegt die Holzhütte? Wie viel Kraft brauche ich um sie in Bewegung zu halten / weiter zu schieben?
Zusatz:
Was bewirkt ein Spanngurt bei der Palette auf der Ladefläche eines LKWs ?
Lösung
1.
ges.: Haftreibungskraft (N)
geg.: M (Masse) = 500g x 12
Reibungszahl Stahl auf Holz (µ) = 0,6
Lösung:
500g x 12 = 6000g = 6 kg
FG= 6kg x 10 = 60 N
FN= 60 N
FHR= µHR x FN = 0,6 x 60 N = 36 N
2.
ges.: M (Masse) in kg,
FGR (N)
geg.: FHR = 1980 N
Lösung:
I.)
FG = µ x FN I /µ
FG / µ = FN =1980 N / 0,6 = 3300N
FN = M x10 I / 10
FN / 10 = M = 3300N / 10 = 330 Kg
II.)
FGR = µGR x FN = 0,35 x 3300 N = 1155 N
Antwort: Um die 330kg schwere Holzhütte in Bewegung zu halten benötigt man 1155 N.
Zusatz: Das Spanngurt erhöht den Anpressdruck der Palette auf der Ladefläche und erhöht damit die Haftreibungskraft zwischen der Palette und der Ladefläche.
Schülerexperiment
Material
- Federkraftmesser (Fzmax = 3 N )
- Holzklotz ( FG = 30 g = FN = 0,30 N)
- halbvolle Duftsanddose ( FG= 455 g = FN = 4,55 N )
- Holzbalken (geschliffen, unlackiert)
Verlauf
- Duftsand auf Holklotz stellen = FN = 0,30N + 4,55 N = 4,85 N)
- gleichmäßig mit Federkraftmesser (FZ) über Holzbalken ziehen = FGR
Beobachtung
- bleibt bis Fz 1,45 N haften = FHR
- sobald es gleitet sinkt die Fz auf 1,30 N = FGR
Berechnung
ges: Reibungkoeffizient (µHR / µGR)
geg: FHR = 1,45 N
FGR = 1,30 N
FN = 4,85 N
Lösung:
FHR = µHR x FN I :FN
FHR / FN = µHR
1,45 N / 4,85 = 0,30
FGR = µGR x FN I :FN
FGR / FN = µGR
1,30 N / 4,85 N = 0,27
Antwort: Bei einem geschliffenen, unlackiertem Holzuntergrund beträgt der Haftreibungskoeffizient 0,30 und der Gleitreibungskoeffizient 0,27.
Quellen
- Wissen: studyflix.de, Formelsammlung
- Video + Bilder: Eigenproduktion