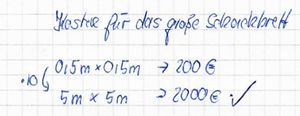Jule Volbers/Studie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (78 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="font-size: 14pt; background-color: #8B8386 ; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: 5px; "> Willkommen auf dem Lernpfad: Maßstäbliches Vergrößern oder Verkleinern | <div style="font-size: 14pt; background-color: #8B8386 ; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: 5px; "> Willkommen auf dem Lernpfad: Maßstäbliches Vergrößern oder Verkleinern - Wie verändern sich Seitenlängen, Flächen und Körper? </div> | ||
[[Datei:Teetasse.jpg|300px|right]] | [[Datei:Teetasse.jpg|300px|right]] | ||
| Zeile 17: | Zeile 17: | ||
{{Box|[[Datei:BildLogoNeu.jpg|150px|right]]Harry-Logo|Harrys Freundin Luna hat ein "Harry-Logo" entworfen. Durch geeignete Zauber kann sie es vergrößern und verkleinern, so dass sie es als Anstecknadel oder auch als Banner verwenden kann. | {{Box|[[Datei:BildLogoNeu.jpg|150px|right]]Harry-Logo|Harrys Freundin Luna hat ein "Harry-Logo" entworfen. Durch geeignete Zauber kann sie es vergrößern und verkleinern, so dass sie es als Anstecknadel oder auch als Banner verwenden kann. | ||
Überlege | |||
Überlege, wie du vorgehen würdest, um das Logo auf die doppelte Größe zu vergrößern bzw. halbe Größe zu verkleinern. | |||
Notiere stichpunktartig, wie sich | |||
* Seitenlängen | * Seitenlängen | ||
* | * Winkel | ||
* Flächen | * Flächen | ||
* | * Seitenverhältnisse | ||
* | * Flächenverhältnisse (z.B. Buchstabe - Umrandung) | ||
verändern. | verändern. | ||
Überprüfe deine Angaben anschließend mit | |||
Überprüfe deine Angaben anschließend mit dem Applet "Logo". | |||
{{Lösung versteckt|Du kannst den Vergrößerungsfaktor - auch '''Skalierungsfaktor''' genannt - mit dem Schiebregler verändern. | {{Lösung versteckt|Du kannst den Vergrößerungsfaktor - auch '''Skalierungsfaktor''' genannt - mit dem Schiebregler verändern. | ||
<br /><ggb_applet id="xaery34n" width="20%" height="20%" border="888888" /> | <br /><ggb_applet id="xaery34n" width="20%" height="20%" border="888888" /> | ||
| Zeile 71: | Zeile 75: | ||
|Farbe={{Farbe|orange}}}} | |Farbe={{Farbe|orange}}}} | ||
Fülle jetzt den Lückentext aus. Kontrolliere deine Lösung und übertrage sie in den Kasten "Maßstäbliches Vergrößern oder Verkleinern von Figuren" in deinem Begleitheft. | Fülle jetzt den Lückentext aus. Kontrolliere deine Lösung und übertrage sie in den Kasten "Skalieren = Maßstäbliches Vergrößern oder Verkleinern von Figuren" in deinem Begleitheft. | ||
| Zeile 83: | Zeile 87: | ||
{{Box|Wie groß ist die Teetasse?|[[Datei:Teetasse.jpg|200px|right]] | {{Box|Wie groß ist die Teetasse?|[[Datei:Teetasse.jpg|200px|right]] | ||
Nachdem Alice einen Zaubertrank getrunken hat, schrumpft sie auf ein Zehntel ihrer Größe. | Nachdem Alice einen Zaubertrank getrunken hat, schrumpft sie auf ein Zehntel ihrer Größe. | ||
# Gib den Skalierungfaktor an, mit dem die Teetasse vergrößert werden musste. | # Gib den Skalierungfaktor an, mit dem die Teetasse für die Dreharbeiten vergrößert werden musste. | ||
# Die originale Teetasse ist ca. 8 cm hoch und hat am oberen Rand einen Umfang von 28 cm. Berechne Höhe und Umfang der vergrößerten Teetasse. | # Die originale Teetasse ist ca. 8 cm hoch und hat am oberen Rand einen Umfang von 28 cm. Berechne Höhe und Umfang der vergrößerten Teetasse. | ||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
| Zeile 97: | Zeile 101: | ||
{{Box|Quadratwachstum 1| | {{Box|Quadratwachstum 1| | ||
''Hinweis: Bei dieser Aufgabe musst du | ''Hinweis: Bei dieser Aufgabe musst du die Tabelle zur Aufgabe "Quadratwachstum 1" in Begleitmaterial ausfüllen. Dabei hilft dir das Geogebraapplet Quadrate 1.''<br /> | ||
So funktioniert das Applet: <br /> | |||
Im Applet "Quadrate 1" siehst du zwei Quadrate mit der Seitenlänge 1 cm, also einem Flächeninhalt von 1 cm². Das rechte Quadrat kannst du vergrößern, indem du den Skalierungsfaktor (2,3 oder 4) passend einstellst. Anschließend kannst du Kopien des kleinen Quadrats erzeugen und das skalierte Quadrat damit "auslegen". Auch Verkleinerungen (0,5 und 0,25) sind möglich. Dazu muss du die Konstruktion eventuell zurücksetzen (Pfeil oben rechts). | |||
{{Lösung versteckt| <ggb_applet id=" bz4xthmv" width="30%" height="30%" border="888888" /> | |||
| Zeile 137: | Zeile 142: | ||
|2= Quadrate 1|3=Quadrate 1}} | |2= Quadrate 1|3=Quadrate 1}} | ||
Nutze das Applet, um die Tabelle zur Aufgabe "Quadratwachstum 1" im Begleitmaterial zu füllen. | |||
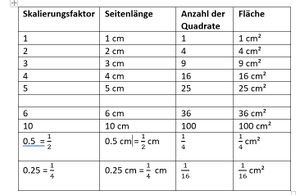
* 1. Fülle die Spalte "Anzahl der Quadrate". | |||
{{Lösung versteckt|1 = Vergrößere das rechte Quadrat zunächst einmal (Skalierung mit einem Faktor k > 1). Für die die Vergrößerungsfaktoren 2, 3 und 4 hilft dir das Applet, die Anzahlen für die Vergrößerungsfaktoren 5,6 und 10 musst du daraus erschließen. | |||
Verkleinere das Quadrat anschließend (Faktoren '''0,5''' (gleich <small>'''<math>\frac{1}{2}</math>'''</small>) und '''0,25''' (gleich <small>'''<math>\frac{1}{4}</math>'''</small>). Du brauchst jetzt nur einen Teil des originalen Quadrats, um die Fläche auszulesen. Finde diesen Anteil heraus. |2= Tipp zu 1.|3=einklappen}} | |||
* 2. Berechne den Flächeninhalt der vergrößerten oder verkleinerten Quadrate mit Hilfe der Anzahl der Quadrate. Trage die Werte in die Spalte "Fläche in cm²" der Tabelle ein. | |||
{{Lösung versteckt|1 = Das originale Quadrat ist das Einheitsquadrat und hat eine Fläche von 1 cm². |2= Tipp zu 2.|3=einklappen}} | |||
* | * 3. Überlege, welcher Zusammenhang zwischen Vergrößerungsfaktor k und Zahl der Quadrate besteht. Gib eine Formel an, mit der sich der Flächeninhalt direkt mit Hilfe des Skalierungsfaktors '''k''' berechnen lässt. Trage sie im Begleitmaterial ein. | ||
Kontrolliere deine Lösung! | Kontrolliere deine Lösung! | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Lösung versteckt|1= [[Datei: | {{Lösung versteckt|1= [[Datei:LösungQuadratwachstum1.jpg|mini|left]] | ||
* Wird das Quadrat mit dem Faktor '''k''' vergrößert, ist die Zahl der Quadrate '''k<sup>2</sup>''' | * Wird das Quadrat mit dem Faktor '''k''' vergrößert, ist die Zahl der Quadrate '''k<sup>2</sup>''' | ||
* Man muss den ursprünglichen Flächeninhalt lediglich mit der Anzahl der Quadrate multiplizieren, um den neuen Flächeninhalt zu erhalten. | * Schiebt man eine Kopie des Originalquadrats auf das verkleinerte Quadrat, erkennt man, dass dass das verkleinerte Quadrat viermal (bzw. sechzehnmal) in das Originalquadrat passen würde. Man benötigt zum Auslegen also nur noch <small><math>\frac{1}{4}</math></small> bzw. <small><math>\frac{1}{16}</math></small> der Originalfläche. | ||
* Man muss den ursprünglichen Flächeninhalt lediglich mit der Anzahl der Quadrate multiplizieren, um den neuen Flächeninhalt zu erhalten. | |||
* Wird ein Quadrat mit der Seitenlänge 1 cm mit dem Faktor '''k''' skaliert, so beträgt der Flächeninhalt '''k<sup>2</sup>'''. Die Formel für den neuen Flächeninhalt '''A<sub>neu</sub> = k<sup>2</sup>.''' | * Wird ein Quadrat mit der Seitenlänge 1 cm mit dem Faktor '''k''' skaliert, so beträgt der Flächeninhalt '''k<sup>2</sup>'''. Die Formel für den neuen Flächeninhalt '''A<sub>neu</sub> = k<sup>2</sup>.''' | ||
* (Begründung für Skalierungsfaktoren kleiner 1: Es ist (<small><math>\frac{1}{2}</math></small>)<sup>2</sup> = <small><math>\frac{1}{4}</math></small>, (<small><math>\frac{1}{4}</math></small>)<sup>2</sup>= <small><math>\frac{1}{16}</math></small>.) | |||
|2= Lösung a |3=einklappen}} | |2= Lösung a |3=einklappen}} | ||
| Zeile 175: | Zeile 172: | ||
{{Box|Quadratwachstum 2| | {{Box|Quadratwachstum 2| | ||
''Hinweis: Bei dieser Aufgabe musst du | ''Hinweis: Bei dieser Aufgabe musst du die Tabelle zur Aufgabe "Quadratwachstum 2" in Begleitheft ausfüllen. Hierbei hilft dir das Geogebraapplet Quadrate 2.'' | ||
''Bei diesem Applet musst du nur den passenden Skalierungsfaktor einstellen.'' | |||
{{Lösung versteckt| <ggb_applet id="ez4stbyn" width="50%" height="50%" border="888888" /> | {{Lösung versteckt| <ggb_applet id="ez4stbyn" width="50%" height="50%" border="888888" /> | ||
| Zeile 210: | Zeile 202: | ||
| Zeile 220: | Zeile 210: | ||
|2= Quadrate 2|3=einklappen}} | |||
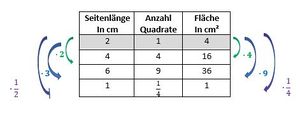
Begründe mit Hilfe des Applets Quadrate 2, dass man mit der gerade entwickelten Idee den Flächeninhalt eines vergrößerten oder verkleinerten Quadrats auch dann berechnen kann, wenn das Originalquadrat eine Seitenlänge ungleich 1 cm hat. Gehe dazu folgendermaßen vor: | |||
* Verdopple, verdreifache und halbiere die Seitenlänge des Quadrats. Berechne den Flächeninhalt mit Hilfe der angezeigten '''Rasterung''' und trage die Ergebnisse (Seitenlängen, Anzahl der Quadrate und Flächeninhalt) in die Tabelle im Begleitheft ein. | |||
* Was stellt du fest, wenn du die Zahl der Quadrate für die Verdopplung/Verdreifachung/Halbierung (mittlere Spalte in den beiden Tabellen) vergleichst? | |||
* Mache dir klar, wie du die Flächeninhalte der vergrößerten oder verkleinerten Quadrate aus dem Flächeninhalt des Originalquadrats und dem Skalierungsfaktor berechnen kannst. Fülle den Lückentext im Begleitheft aus. | |||
Kontrolliere dann deine Lösung. | |||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Lösung versteckt|1= [[Datei:Quadratwachstum2 neu.jpg|mini| | {{Lösung versteckt|1= [[Datei:Quadratwachstum2 neu.jpg|mini|left]] Die Anzahl der Quadrate bleibt beim Skalieren gleich. Sie hängt nicht vom Flächeninhalt der Originalfigur ab. | ||
Die Formel für den Flächeninhalt der vergrößerten oder verkleinerten Rechteck ist ''' | Man kann also den Flächeninhalt des vergrößerten oder verkleinerten Quadrats berechnen, indem man den ursprünglichen '''Flächeninhalt''' mit der Zahl der Quadrate multipliziert. | ||
Die Formel für den Flächeninhalt der vergrößerten oder verkleinerten Rechteck ist '''Flächeinhalt <sub>neu</sub> = Flächeninhalt <sub>alt</sub> ⋅ k²'''. | |||
In unserem Beispiel hat das ursprüngliche Quadrat den Flächeninhalt 4 cm². Die mit dem Faktor k vergrößerten oder verkleinerten Quadrate haben also einen Flächeninhalt von 4⋅ k² | |||
|2= Lösung |3=einklappen}} | |2= Lösung |3=einklappen}} | ||
| Zeile 268: | Zeile 238: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Wird die Seitenlänge eines Quadrats | Wird die Seitenlänge eines Quadrats | ||
*verdoppelt, so wächst der Flächeninhalt auf das ''' | *verdoppelt, so wächst der Flächeninhalt auf das '''Vierfache''' | ||
*verdreifacht, so wächst der Flächeninhalt auf das ''' | *verdreifacht, so wächst der Flächeninhalt auf das '''Neunfache''' | ||
*verzehnfacht, so wächst der Flächeninhalt auf das ''' | *verzehnfacht, so wächst der Flächeninhalt auf das '''Hundertfache''' | ||
*halbiert, so schrumpft der Flächeninhalt auf '''ein Viertel''' | *halbiert, so schrumpft der Flächeninhalt auf '''ein Viertel''' | ||
Der Flächeninhalt eines Quadrats wächst also '''quadratisch''' zum Skalierungsfaktor. Der Flächeninhalt wird berechnet mit | Der Flächeninhalt eines Quadrats wächst also '''quadratisch''' zum Skalierungsfaktor. Der Flächeninhalt wird berechnet mit | ||
| Zeile 280: | Zeile 250: | ||
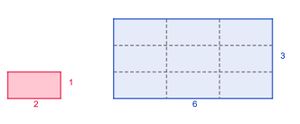
{{Box|Flächenwachstum von Rechtecken| [[Datei:Rechteck2.jpg|mini]] Auch Rechtecke kann man rastern. Erkläre mit Hilfe der Abbildung, dass auch der Flächeninhalt von Rechtecken bei Skalieren mit dem Faktor k² wächst. | {{Box|Flächenwachstum von Rechtecken| [[Datei:Rechteck2.jpg|mini]] Auch Rechtecke kann man rastern. Erkläre mit Hilfe der Abbildung, dass auch der Flächeninhalt von Rechtecken bei Skalieren mit dem Faktor k² wächst. | ||
{{Lösung versteckt| 1 = Im Beispiel werden die Seitenlängen verdreifacht. Das bedeutet, dass sowohl in der Breite als auch der Länge drei kleine Rechtecke in das vergrößerte Reckteck passen. Das sind insgesamt 3⋅3 = 3²=9 Rechtecke. | {{Lösung versteckt| 1 = Im Beispiel werden die Seitenlängen verdreifacht. Das bedeutet, dass sowohl in der Breite als auch der Länge drei kleine Rechtecke in das vergrößerte Reckteck passen. Das sind insgesamt 3⋅3 = 3²=9 Rechtecke. Der Flächeninhalt wird also neunmal größer. | ||
|2= Lösung |3=einklappen}} | |2= Lösung |3=einklappen}} | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
| Zeile 289: | Zeile 259: | ||
{{Box|See| | {{Box|See| | ||
Untersuche, wie der Flächeninhalt des Bildes des Sees beim Vergrößern wächst mit Hilfe des Applets. Bearbeite dazu die Aufgaben, die du unter dem Applet findest. | Untersuche, wie der Flächeninhalt des Bildes des Sees beim Vergrößern wächst mit Hilfe des Applets. Bearbeite dazu die Aufgaben, die du unter dem Applet findest. Kontrolliere nach jeder Aufgabe deine Lösung. | ||
<ggb_applet id="tqvtqcjw" width="30%" height="30%" /> | <ggb_applet id="tqvtqcjw" width="30%" height="30%" /> | ||
# Schätze den Flächeninhalt des Sees durch die Fläche der Kästchen ab. Ein Kästchen hat eine Seitenlänge von 0,5 cm. | # Schätze den Flächeninhalt des Sees durch die Fläche der Kästchen ab. Ein Kästchen hat eine Seitenlänge von 0,5 cm. | ||
| Zeile 298: | Zeile 268: | ||
{{Lösung versteckt|1 = Überlege, mit welchem Faktor die Seitenlängen (ausgehend von der Originalzeichnung) skaliert wurden. Nutze dann dein Wissen über das Wachstum von Flächen. |2= Tipp 5.|3=einklappen}} | {{Lösung versteckt|1 = Überlege, mit welchem Faktor die Seitenlängen (ausgehend von der Originalzeichnung) skaliert wurden. Nutze dann dein Wissen über das Wachstum von Flächen. |2= Tipp 5.|3=einklappen}} | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Lösung versteckt|1 = Der Flächeninhalt des Sees entspricht ca. 22 Kästchen | {{Lösung versteckt|1 = Der Flächeninhalt des Sees entspricht ca. 22 Kästchen. Ein Kästchen hat eine Fläche von 0,25 cm². Also hat der See einen Flächeninhalt von 22⋅0,25 cm² = 5,5 cm²|2= Lösung 1.|3=einklappen}} | ||
{{Lösung versteckt|1= Der Flächeninhalt des Sees entspricht auch hier ca. 22 Kästchen. Ein Kästchen hat eine Fläche von 1 cm². Also hat der See eine Fläche von 22⋅1 cm²= 22 cm²|2= Lösung 2.|3=einklappen}} | {{Lösung versteckt|1= Der Flächeninhalt des Sees entspricht auch hier ca. 22 Kästchen. Ein Kästchen hat eine Fläche von 1 cm². Also hat der See eine Fläche von 22⋅1 cm²= 22 cm²|2= Lösung 2.|3=einklappen}} | ||
{{Lösung versteckt|1 = Der Skalierungsfaktor ist 2, weil die Seitenlängen der Quadrate und somit alle Längen verdoppelt wurden.|2= Lösung 3.|3=einklappen}} | {{Lösung versteckt|1 = Der Skalierungsfaktor ist 2, weil die Seitenlängen der Quadrate und somit alle Längen verdoppelt wurden.|2= Lösung 3.|3=einklappen}} | ||
| Zeile 305: | Zeile 275: | ||
{{Lösung versteckt|1 = Der Skalierungsfaktor beträgt 20. Der Flächeninhalts wächst also auf das 400fache. Also beträgt der Flächeninhalt des Sees | {{Lösung versteckt|1 = Der Skalierungsfaktor beträgt 20. Der Flächeninhalts wächst also auf das 400fache. Also beträgt der Flächeninhalt des Sees | ||
5,5 cm² ⋅ 400 = 2200 cm²|2= Lösung 5.|3=einklappen}} | 5,5 cm² ⋅ 400 = 2200 cm²|2= Lösung 5.|3=einklappen}} | ||
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten " | |||
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "So verändern sich Flächen beim Skalieren" in deinem Begleitheft. | |||
{{Box|1=Merke: So verändern sich Flächen beim Skalieren | {{Box|1=Merke: So verändern sich Flächen beim Skalieren | ||
| Zeile 318: | Zeile 291: | ||
|3=Merksatz}} | |3=Merksatz}} | ||
{{Box|Idee|Mit Hilfe des Skalierungsfaktors kannst du die Flächeninhalte beliebiger vergrößerter oder verkleinerter Figuren sehr schnell berechnen|Unterrichtsidee }} | {{Box|Idee|Mit Hilfe des Skalierungsfaktors kannst du die Flächeninhalte beliebiger vergrößerter oder verkleinerter Figuren sehr schnell berechnen.|Unterrichtsidee }} | ||
{{Box|Flächeninhalte schnell berechnen| | {{Box|Flächeninhalte schnell berechnen| | ||
''Hinweis: Bei dieser Aufgabe musst du die Ergebnisse im | ''Hinweis: Bei dieser Aufgabe musst du die Ergebnisse in die Tabelle: "Flächeninhalte schnell berechnen" im Begleitheft eintragen.'' | ||
Berechne die neuen Flächeninhalte mit Hilfe des Skalierungsfaktors. Trage Rechnung und Ergebnisse in die Tabelle zur Aufgabe | |||
# Ein Quadrat hat einen Flächeninhalt von 32 cm². Welchen Flächeninhalt das Quadrat, wenn es mit dem Faktor 1/4 verkleinert wird | Berechne die neuen Flächeninhalte mit Hilfe des Skalierungsfaktors. Trage '''Rechnung''' und '''Ergebnisse''' in die Tabelle zur Aufgabe im Begleitheft ein. | ||
# Ein Quadrat hat einen Flächeninhalt von 32 cm². Welchen Flächeninhalt hat das Quadrat, wenn es mit dem Faktor 1/4 verkleinert wird? | |||
# Ein Kreis hat einen Flächeninalt von 10 cm². Welchen Flächeninhalt hat der Kreis, wenn er mit dem Faktor fünf vergrößert wird? | # Ein Kreis hat einen Flächeninalt von 10 cm². Welchen Flächeninhalt hat der Kreis, wenn er mit dem Faktor fünf vergrößert wird? | ||
# [[Datei:Eule.jpg|100px|right]] Die abgebildete Eule hat einen Flächeninhalt von 0,25 m². Welchen Flächeninhalt hat das mit dem Faktor 3 vergrößerte Bild der Eule? | # [[Datei:Eule.jpg|100px|right]] Die abgebildete Eule hat einen Flächeninhalt von 0,25 m². Welchen Flächeninhalt hat das mit dem Faktor 3 vergrößerte Bild der Eule? | ||
| Zeile 330: | Zeile 304: | ||
Kontrolliere anschließend deine Lösung. | Kontrolliere anschließend deine Lösung. | ||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
{{Lösung versteckt|1 = # <small>'''<math>\frac{1}{4}</math>'''</small>² = <small>'''<math>\frac{1}{16}</math>'''</small>; 32⋅ <small>'''<math>\frac{1}{16}</math>'''</small>= 2. Das Quadrat hat einen Flächeninhalt von 2 cm³ | {{Lösung versteckt|1 = # <small>'''<math>\frac{1}{4}</math>'''</small>² = <small>'''<math>\frac{1}{16}</math>'''</small>; 32⋅ <small>'''<math>\frac{1}{16}</math>'''</small>= 2. Das Quadrat hat einen Flächeninhalt von 2 cm³ | ||
# 5² = 25; 10 ⋅ 25 = 250. Der Kreis hat einen Flächeninhalt von 250 cm². | # 5² = 25; 10 ⋅ 25 = 250. Der Kreis hat einen Flächeninhalt von 250 cm². | ||
| Zeile 335: | Zeile 310: | ||
# Der Skalierungsfaktor ist 2; 2²= 4; 0,6 ⋅ 4 = 2,4. Die Tischdecke hat einen Flächeninhalt von 2,4 m². | # Der Skalierungsfaktor ist 2; 2²= 4; 0,6 ⋅ 4 = 2,4. Die Tischdecke hat einen Flächeninhalt von 2,4 m². | ||
# Der Skalierungsfaktor ist 0,5. 0,5² = 0,25; 2000 ⋅ 0,25 = 500. Die Pizza hat eine Fläche von 500 cm². |2= Lösung|3=einklappen}} | # Der Skalierungsfaktor ist 0,5. 0,5² = 0,25; 2000 ⋅ 0,25 = 500. Die Pizza hat eine Fläche von 500 cm². |2= Lösung|3=einklappen}} | ||
=='''3. So verändern sich Körper beim Vergrößern und Verkleinern'''== | =='''3. So verändern sich Körper beim Vergrößern und Verkleinern'''== | ||
{{Box|Idee|Auch für den Rauminhalt (das Volumen) von Körpern gibt es eine Gesetzmäßigkeit, mit der die Rauminhalte beim Vergrößern oder Verkleinern wachsen bzw. schrumpfen. Diese Gesetzmäßigkeit sollst du am Beispiel eines Würfels erarbeiten:|Unterrichtsidee }} | {{Box|Idee|Auch für den Rauminhalt (das Volumen) von Körpern gibt es eine Gesetzmäßigkeit, mit der die Rauminhalte beim Vergrößern oder Verkleinern wachsen bzw. schrumpfen. Diese Gesetzmäßigkeit sollst du am Beispiel eines Würfels erarbeiten:|Unterrichtsidee }} | ||
{{Box|Würfelwachstum 1|[[Datei:Würfel.jpg|mini|right]] | {{Box|Würfelwachstum 1|[[Datei:Würfel.jpg|mini|right]] | ||
''Hinweis: Bei dieser Aufgabe musst du | ''Hinweis: Bei dieser Aufgabe musst du die Tabelle zur Aufgabe "Würfelwachstum 1" im Begleitheft ausfüllen. '' | ||
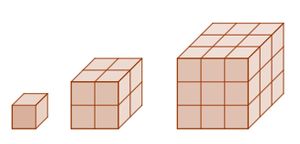
Der kleine Würfel hat eine Seitenlänge von 1 cm. Der zweite und dritte Würfel entstehen, indem kleine Würfel aneinandergeklebt werden. | Der kleine Würfel hat eine Seitenlänge von 1 cm. Der zweite und dritte Würfel entstehen, indem kleine Würfel aneinandergeklebt werden. | ||
# Trage zunächst die Seitenlängen und den Flächeninhalt der Seiten des zweiten und dritten Würfels in die Tabelle zur Aufgabe in deinem Begleitheft ein. | # Trage zunächst die Seitenlängen und den Flächeninhalt der Seiten des zweiten und dritten Würfels in die Tabelle zur Aufgabe in deinem Begleitheft ein. | ||
| Zeile 345: | Zeile 323: | ||
# Ergänze die Werte für den "Viererwürfel" und für den "Sechserwürfel". | # Ergänze die Werte für den "Viererwürfel" und für den "Sechserwürfel". | ||
# Erkläre mit Hilfe der Tabelle, wie das Volumen eines beliebigen Würfels wächst, wenn man die Seitenlänge des Würfels verdoppelt bzw. verdreifacht. | # Erkläre mit Hilfe der Tabelle, wie das Volumen eines beliebigen Würfels wächst, wenn man die Seitenlänge des Würfels verdoppelt bzw. verdreifacht. | ||
# Überlege, mit welchem Faktor man das Volumen multiplizieren muss, wenn man einen | # Überlege, mit welchem Faktor man das Volumen multiplizieren muss, wenn man einen Würfel mit dem Faktor k skaliert. Notiere ihn in deinem Begleitheft im Kasten zur Aufgabe. | ||
Kontrolliere dein Ergebnis. | Kontrolliere dein Ergebnis. | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
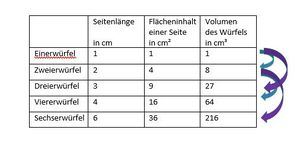
{{Lösung versteckt|1=1. bis 3.: Siehe Tabelle. [[Datei:Würfelwachstum3.jpg|300px|right]] | {{Lösung versteckt|1=1. bis 3.: Siehe Tabelle. [[Datei:Würfelwachstum3.jpg|300px|right]] | ||
4: In der Tabelle kann man die Werte für zwei Verdopplungen ablesen (blaue Pfeile). Das Volumen wächst jeweils auf das Achtfache. | 4: In der Tabelle kann man die Werte für zwei Verdopplungen ablesen (blaue Pfeile). Das Volumen wächst jeweils auf das Achtfache. | ||
Ebenso kann man die Werte für zwei Verdreifachungen ablesen(lila Pfeile). Das Volumen wächst jeweils auf das Siebenundzwanzigfache. | Ebenso kann man die Werte für zwei Verdreifachungen ablesen(lila Pfeile). Das Volumen wächst jeweils auf das Siebenundzwanzigfache. | ||
5. Für eine Verdopplung - also k = 2 ist der Faktor 2²=8. Für eine | 5. Für eine Verdopplung - also k = 2 ist der Faktor 2²=8. Für eine Verdreifachung - also k = 3 ist der Faktor 3³ = 27. Allgemein gilt: Skaliert man einen Würfel mit dem Faktor k, muss man das Volumen mit dem Faktor k³ multiplizieren. (Man sagt auch: Rauminhalte wachsen kubisch.) | ||
|2= Lösung |3=einklappen}} | |2= Lösung |3=einklappen}} | ||
{{Box|1=Würfelwachstum 2|2= <div class="lueckentext-quiz"> | |||
{{Box|1 = Würfelwachstum 2| | |||
2 = Hier kannst du dir das Würfelwachstum noch einmal veranschaulichen. Fülle mit Hilfe der Schieberegler den großen Würfel vollständig mit den kleinen Würfeln aus. Beobachte, wie sich die Würfelzahlen verändern. Fülle dannn den Lückentext. | |||
<ggb_applet id="ubtaep7k" width="30%" height="30%" /> | |||
<div class="lueckentext-quiz"> | |||
Der kleine Würfel hat eine Seitenlänge von 2 cm, also ein Volumen von '''8 cm³'''. Um eine Bodenreihe des großen Würfels mit kleinen Würfeln zu füllen, benötigt man '''5''' kleine Würfel, um den ganzen Boden zu füllen '''25''' kleine Würfel. Um den ganzen Würfel zu füllen, muss man diese untere Schicht '''5mal''' stapeln. Also sind '''125''' kleine Würfel nötig, um den großen Würfel zu füllen. Der große Würfel hat also ein Volumen von <br /> '''125''' ⋅ '''8'''cm³ = '''1000'''cm³ | |||
</div> | |||
|3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Würfelwachstum 3" in deinem Begleitheft. | |||
{{Box|1=Würfelwachstum 3|2= <div class="lueckentext-quiz"> | |||
Wenn man die Seitenlängen eines Würfels | Wenn man die Seitenlängen eines Würfels | ||
*verdoppelt, so wächst das Volumen auf das ''' | *verdoppelt, so wächst das Volumen auf das '''Achtfache''' | ||
*verdreifacht, so wächst das Volumen auf das ''' | *verdreifacht, so wächst das Volumen auf das '''Siebenundzwanzigfache''' | ||
*verzehnfacht, so wächst das Volumen auf das ''' | *verzehnfacht, so wächst das Volumen auf das '''Tausendfache''' | ||
*halbiert, so schrumpft das Volumen auf '''ein Achtel''' | *halbiert, so schrumpft das Volumen auf '''ein Achtel''' | ||
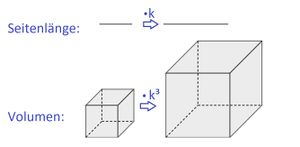
Skaliert man einen Würfel mit dem Faktor k, so ist das neue Volumen | Skaliert man einen Würfel mit dem Faktor k, so ist das neue Volumen | ||
| Zeile 367: | Zeile 367: | ||
{{Box|Idee|Dieses Wachstumsprinzip gilt für beliebige Körper. Man kann alle Überlegungen zu den Flächen auf den "3D-Fall" übertragen. |Unterrichtsidee }} | {{Box|Idee|Dieses Wachstumsprinzip gilt für beliebige Körper. Man kann alle Überlegungen zu den Flächen auf den "3D-Fall" übertragen. |Unterrichtsidee }} | ||
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in die Box "So verändern sich Körper beim Skalieren" im | |||
{{Box|Kugel| | |||
Auch für Körper kann man sich eine Rasterung vorstellen. Jeden Körper kann man sich durch viele kleine Würfel angenähert vorstellen. Ein Beispiel siehst du in der Abbildung. Erkläre in eigenen Worten, warum das Volumen des Körpers sich verachtfacht, wenn man ihn mit dem Faktor 2 vergrößert. Notiere deine Überlegungen auf ein Extrablatt. | |||
[[Datei:KugelRast.jpg|mini]] | |||
{{Lösung versteckt|1 = Wenn man die Kugel mit dem Faktor 2 skaliert, verdoppeln sich alle Seitenlängen. Weil die Seitenlängen jedes Würfels sich verdoppelt, wächst das Volumen jedes Würfels auf das Achtfache. Damit verachtfacht sich auch das Volumen der Kugel. |3=einklappen}} | |||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in die Box "So verändern sich Körper beim Skalieren" im Begleitheft. | |||
{{Box|1=Merke: So verändern sich Körper beim Skalieren | {{Box|1=Merke: So verändern sich Körper beim Skalieren | ||
| Zeile 382: | Zeile 390: | ||
{{Box|Idee|Auch Rauminhalte lassen sich beim Vergrößern und Verkleinern schnell mit Hilfe des Skalierungsfaktors berechnen. |Unterrichtsidee }} | {{Box|Idee|Auch Rauminhalte lassen sich beim Vergrößern und Verkleinern schnell mit Hilfe des Skalierungsfaktors berechnen. |Unterrichtsidee }} | ||
{{Box|Rauminhalte schnell berechnen|Berechne das neue Volumen jeweils mit Hilfe des Skalierungsfaktors: | |||
{{Box|Rauminhalte schnell berechnen| | |||
''Hinweis: Bei dieser Aufgabe musst du die Tabelle zur Aufgabe "Würfelwachstum 1" im Begleitheft ausfüllen. '' | |||
Berechne das neue Volumen jeweils mit Hilfe des Skalierungsfaktors: | |||
# Ein Würfel hat ein Volumen von 8cm³. Welches Volumen hat ein mit dem Faktor 0,5 verkleinerter Würfel? | # Ein Würfel hat ein Volumen von 8cm³. Welches Volumen hat ein mit dem Faktor 0,5 verkleinerter Würfel? | ||
# Tom hat Glasmurmeln verschiedener Größen. Die kleinste Glasmurmel wiegt 4 Gramm. Wie schwer ist die größte Murmel, deren Durchmesser fünfmal so groß ist? | # Tom hat Glasmurmeln verschiedener Größen. Die kleinste Glasmurmel wiegt 4 Gramm. Wie schwer ist die größte Murmel, deren Durchmesser fünfmal so groß ist? | ||
| Zeile 391: | Zeile 403: | ||
# Skalierungsfaktor 2: 2³=8: 400 ⋅ 8=3200. Die Vase hat ein Volumen von 3200 ml = 3,2 l. | # Skalierungsfaktor 2: 2³=8: 400 ⋅ 8=3200. Die Vase hat ein Volumen von 3200 ml = 3,2 l. | ||
Skalierungsfaktor 0,5: 0,5³=0,125; 400 ⋅ 0,125= 50. Die Vase hat ein Volumen von 50 ml. |2= Lösung|3=einklappen}} | Skalierungsfaktor 0,5: 0,5³=0,125; 400 ⋅ 0,125= 50. Die Vase hat ein Volumen von 50 ml. |2= Lösung|3=einklappen}} | ||
=='''4. Längen, Flächen und | |||
=='''4. Längen, Flächen- und Rauminhalte beim Skalieren - vernetzte Aufgaben'''== | |||
Lies die Zusammenfassung und übertrage die fett gedruckten Worte in die Box "So verändern sich Längen, Flächeninhalte und Volumina beim Skalieren" | Lies die Zusammenfassung und übertrage die fett gedruckten Worte in die Box "So verändern sich Längen, Flächeninhalte und Volumina beim Skalieren" | ||
{{Box|Zusammenfassung: So verändern sich Längen, Flächeninhalte und | |||
{{Box|Zusammenfassung: So verändern sich Längen, Flächeninhalte und Rauminhalte beim Skalieren| | |||
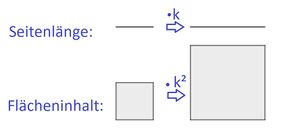
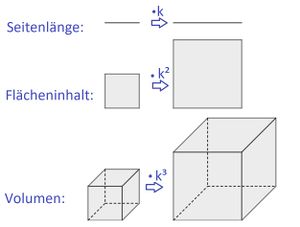
[[Datei:MerksatzZusammenfassung.jpg|mini|left]] Beim Skalieren dehnen sich Längen in eine Richtung aus, Flächen in zwei Richtungen und Volumen in drei Richtungen. Deshalb berechnet man beim Skalieren | [[Datei:MerksatzZusammenfassung.jpg|mini|left]] Beim Skalieren dehnen sich Längen in eine Richtung aus, Flächen in zwei Richtungen und Volumen in drei Richtungen. Deshalb berechnet man beim Skalieren | ||
* '''Längen''' durch '''Multiplikation''' mit dem Faktor '''k''' | * '''Längen''' durch '''Multiplikation''' mit dem Faktor '''k''' | ||
| Zeile 401: | Zeile 416: | ||
{{Box|Das Riesenschachbrett.|[[Datei:Schachbrett_shutterstock_87669796.jpg|150px|right]] | {{Box|Das Riesenschachbrett.|[[Datei:Schachbrett_shutterstock_87669796.jpg|150px|right]] | ||
''Hinweis: Für diese Aufgabe benötigst du | ''Hinweis: Für diese Aufgabe benötigst du die die Tabelle zur Aufgabe "Das Riesenschachbrett" im Begleitheft.'' | ||
Die auf ein Zehntel ihrer Größe geschrumpfte Alice muss gegen Schachfiguren kämpfen. Für das Set musste ein entsprechend großes Schachbrett angefertigt werden. | Die auf ein Zehntel ihrer Größe geschrumpfte Alice muss gegen Schachfiguren kämpfen. Für das Set musste ein entsprechend großes Schachbrett angefertigt werden. | ||
[[Datei:Aufgabe Schach.jpg|150|left]] | [[Datei:Aufgabe Schach.jpg|150|left]] | ||
In der Tabelle zu dieser Aufgabe im | In der Tabelle zu dieser Aufgabe im Begleitheft findest du die Angaben zum originalen Schachbrett. | ||
Gib den Skalierungsfaktor an und berechne dann alle Maße und Gewichte für das vergrößerte Schachbrett. Trage alle Ergebnisse in die Tabelle ein. | |||
Kontrolliere anschließend deine Lösung. | Kontrolliere anschließend deine Lösung. | ||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
[[Datei:SchachbrettLösungen.jpg|200]] | [[Datei:SchachbrettLösungen.jpg|200]] | ||
| Zeile 413: | Zeile 431: | ||
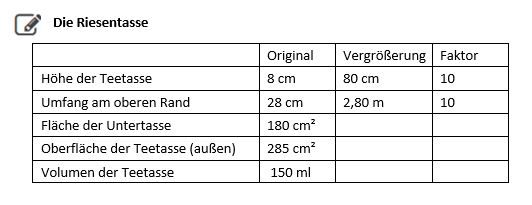
{{Box|Die Riesentasse |[[Datei:Teetasse.jpg|150px|right]] | {{Box|Die Riesentasse |[[Datei:Teetasse.jpg|150px|right]] | ||
''Hinweis: Für diese Aufgabe benötigst du | ''Hinweis: Für diese Aufgabe benötigst du die die Tabelle zur Aufgabe "Die Riesentasse" im Begleitheft. | ||
[[Datei:Riesentasse.jpg|200|left]] | [[Datei:Riesentasse.jpg|200|left]] | ||
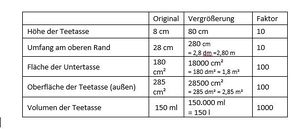
Auch die Teetasse musste mit dem Faktor 10 vergrößert werden. In der Tabelle zu dieser Aufgabe im Begleitmaterial findest du | |||
Auch die Teetasse musste mit dem Faktor 10 vergrößert werden. | |||
In der Tabelle zu dieser Aufgabe im Begleitmaterial findest du die Angaben zur originalen Teetasse. Berechne alle Flächenmaße und das Volumen der vergrößerten Tasse. Trage alle Ergebnisse in die Tabelle ein. | |||
|Üben|Farbe={{Farbe|orange|heller}}}} | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
| Zeile 436: | Zeile 456: | ||
{{Box|Sprinteraufgabe 3: Zu viel Gewicht? | | {{Box|Sprinteraufgabe 3: Zu viel Gewicht? | | ||
[[Datei:Shutterstock 323593550.jpg|mini]] | [[Datei:Shutterstock 323593550.jpg|mini]] | ||
Die auf ein Zehntel ihrer Größe geschrumpfte Alice fällt in ein Aquarium. Für die Filmkulisse soll das abgebildete Aquarium in zehnfacher Größe nachgebaut und mit Wasser gefüllt werden. Die Bühnenbauer befürchten, dass das Aquarium dann zu schwer für die Plattform wird, auf der es stehen soll. Das Aquarium ist 60 cm breit, 30 cm tief und 50 cm hoch. Es wiegt leer 12 kg. Die Plattforn darf mit | Die auf ein Zehntel ihrer Größe geschrumpfte Alice fällt in ein Aquarium. Für die Filmkulisse soll das abgebildete Aquarium in zehnfacher Größe nachgebaut und mit Wasser gefüllt werden. Die Bühnenbauer befürchten, dass das Aquarium dann zu schwer für die Plattform wird, auf der es stehen soll. Das Aquarium ist 60 cm breit, 30 cm tief und 50 cm hoch. Es wiegt leer 12 kg. Die Plattforn darf mit 100 t belastet werden. | ||
Prüfe, ob die Bühnenbauer mit ihrer Befürchtung Recht haben. | Prüfe, ob die Bühnenbauer mit ihrer Befürchtung Recht haben. | ||
|Experimentieren|Farbe={{Farbe |komplementär |dunkel}}}} | |Experimentieren|Farbe={{Farbe |komplementär |dunkel}}}} | ||
{{Lösung versteckt|1= Annahme: Das Becken wird bis 5 cm unterhalb des Randes gefüllt. Dann wären im kleinen Becken 81 l Wasser (60cm ⋅ 30cm ⋅45cm = 85000cm³ = 81000ml = 81l). | |||
In das vergrößerte Becken müsste man dann 81l⋅1000 = 81000 l füllen. | {{Lösung versteckt|1= Annahme: Das Becken wird bis 5 cm unterhalb des Randes gefüllt. Dann wären im kleinen Becken 81 l Wasser (60cm ⋅ 30cm ⋅45cm = 85000cm³ = 81000ml = 81l). In das vergrößerte Becken müsste man dann 81l⋅1000 = 81000 l füllen. | ||
Die Wasserfüllung hat dann (unter normalen Bedingungen ein Gewicht von 81000 kg = 81 Tonnen. | Die Wasserfüllung hat dann (unter normalen Bedingungen ein Gewicht von 81000 kg = 81 Tonnen. | ||
Schwieriger ist es, das Gewicht des Aquariums abzuschätzen, weil wir nicht wissen, ob | Schwieriger ist es, das Gewicht des Aquariums abzuschätzen, weil wir nicht wissen, ob | ||
# das gleiche Material verwendet | #das gleiche Material verwendet wird und | ||
# die Glasdicke der Seiten ebenfalls verzehnfacht wird. | #die Glasdicke der Seiten ebenfalls verzehnfacht wird. | ||
Setzt man beides voraus, wächst das Gewicht des Aquariums ebenfalls mit dem Faktor 1000 (die Seitenflächen sind als Körper zu betrachten). | |||
Setzt man beides voraus, wächst das Gewicht des Aquariums ebenfalls mit dem Faktor 1000 (die Seitenflächen sind als Körper zu betrachten). | |||
Das Aquarium würde also 12000 kg = 12 t wiegen. | Das Aquarium würde also 12000 kg = 12 t wiegen. | ||
Insgesamt würde das gefüllte Aquarium also 93 t wiegen und die Traglast des Podestes wäre groß genug (auch für die Schauspielerin und eventuell Personen aus dem Filmteam samt Ausrüstung). | Insgesamt würde das gefüllte Aquarium also 93 t wiegen und die Traglast des Podestes wäre groß genug (auch für die Schauspielerin und eventuell Personen aus dem Filmteam samt Ausrüstung). | ||
Es bleiben jedoch Unsicherheiten: | Es bleiben jedoch Unsicherheiten: | ||
* Laut unsere Annahme wurde es ja nur bis 50 cm unterhalb des Randes gefüllt. Würde das Becken bis zum Rand gefüllt, wären dies noch 9000 l Wasser, also 9 Tonnen zusätzlich. Dann wäre die Traglast des Podestes überschritten. | *Laut unsere Annahme wurde es ja nur bis 50 cm unterhalb des Randes gefüllt. Würde das Becken bis zum Rand gefüllt, wären dies noch 9000 l Wasser, also 9 Tonnen zusätzlich. Dann wäre die Traglast des Podestes überschritten. | ||
* Sollte das große Aquarium am Boden mit Steinen (statt Kies) gefüllt werden, würde das Aquarium schwerer werden. Nimmt man beispielsweise an, dass die unteren 50 cm (5 cm im Original) des Beckens mit Steinen gefüllt würden, würde sich das Gewicht um 18 Tonnen erhöhen (Faustformel: Steine wiegen etwa dreimal so viel wie Wasser.). Hier wäre die Traglast deutlich überschritten. | *Sollte das große Aquarium am Boden mit Steinen (statt Kies) gefüllt werden, würde das Aquarium schwerer werden. Nimmt man beispielsweise an, dass die unteren 50 cm (5 cm im Original) des Beckens mit Steinen gefüllt würden, würde sich das Gewicht um 18 Tonnen erhöhen (Faustformel: Steine wiegen etwa dreimal so viel wie Wasser.). Hier wäre die Traglast deutlich überschritten. | ||
Daher sind die Bedenken der Bühnenbauer nicht unberechtigt. | Daher sind die Bedenken der Bühnenbauer nicht unberechtigt. | ||
|2= Lösung|3=einklappen}} | |||
Aktuelle Version vom 11. Mai 2023, 06:17 Uhr
In vielen Filmen spielen besonders große oder kleine Helden oder Heldinnen eine wichtige Rolle. Bekannte Beispiele sind der Waldhüter und Halbriese Hagrid der Harry-Potter-Filme oder die Titelfigur Alice aus Alice im Wunderland, die im Laufe der Handlung auf ein Zehntel ihrer Größe schrumpft. Zur Darstellung der Größenverhältnisse wird oft mit großem Aufwand die Kulisse in einer kleineren oder größeren Version nachgebaut.
Doch worauf muss man achten, damit der Nachbau der Kulisse gelingt?
Zur Beantwortung der Frage sollst du untersuchen, wie sich Längen, Flächen, Körper und Winkel beim Vergrößern oder Verkleinern verändern.
1. korrektes Vergrößern und Verkleinern. Worauf kommt es an?
Fülle jetzt den Lückentext aus. Kontrolliere deine Lösung und übertrage sie in den Kasten "Skalieren = Maßstäbliches Vergrößern oder Verkleinern von Figuren" in deinem Begleitheft.
- Der Skalierungsfaktor beträgt 10.
- Die Seitenlängen müssen mit dem Faktor 10 multipliziert werden. Die vergrößerte Teetasse ist 80 cm hoch und hat am oberen Rand einen Umfang von 280 cm = 2,80 m.
2. Wie verändern sich Flächen beim Vergrößern oder Verkleinern?
- Wird das Quadrat mit dem Faktor k vergrößert, ist die Zahl der Quadrate k2
- Schiebt man eine Kopie des Originalquadrats auf das verkleinerte Quadrat, erkennt man, dass dass das verkleinerte Quadrat viermal (bzw. sechzehnmal) in das Originalquadrat passen würde. Man benötigt zum Auslegen also nur noch bzw. der Originalfläche.
- Man muss den ursprünglichen Flächeninhalt lediglich mit der Anzahl der Quadrate multiplizieren, um den neuen Flächeninhalt zu erhalten.
- Wird ein Quadrat mit der Seitenlänge 1 cm mit dem Faktor k skaliert, so beträgt der Flächeninhalt k2. Die Formel für den neuen Flächeninhalt Aneu = k2.
- (Begründung für Skalierungsfaktoren kleiner 1: Es ist ()2 = , ()2= .)
Man kann also den Flächeninhalt des vergrößerten oder verkleinerten Quadrats berechnen, indem man den ursprünglichen Flächeninhalt mit der Zahl der Quadrate multipliziert. Die Formel für den Flächeninhalt der vergrößerten oder verkleinerten Rechteck ist Flächeinhalt neu = Flächeninhalt alt ⋅ k².
In unserem Beispiel hat das ursprüngliche Quadrat den Flächeninhalt 4 cm². Die mit dem Faktor k vergrößerten oder verkleinerten Quadrate haben also einen Flächeninhalt von 4⋅ k²
Beträgt die Seitenlänge des skalierten Quadrats 3 cm, so ist der Skalierungsfaktor k = 1,5.
Die neue Fläche beträgt 9 cm² . Es ist 9 = 4 ⋅ 1,5² = 4 ⋅ 2,25.
Der Flächeninhalt wächst auf das Vierfache. Erklärung: Die Seitenlänge der Quadrate hat sich verdoppelt, also vervierfacht sich der Flächeninhalt der Quadrate. Da beim Skalieren das Verhältnis von Flächeninhalt zueinander gleichbleibt, vervierfacht sich auch der Flächeninhalts des Sees.
Hinweis: Dies sieht man auch, wenn man die Ergebnisse für den Flächeninhalt aus a und b miteinander vergleicht.Der Skalierungsfaktor beträgt 20. Der Flächeninhalts wächst also auf das 400fache. Also beträgt der Flächeninhalt des Sees
5,5 cm² ⋅ 400 = 2200 cm²
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "So verändern sich Flächen beim Skalieren" in deinem Begleitheft.
- ² = ; 32⋅ = 2. Das Quadrat hat einen Flächeninhalt von 2 cm³
- 5² = 25; 10 ⋅ 25 = 250. Der Kreis hat einen Flächeninhalt von 250 cm².
- 3² = 9; 0,25 ⋅ 9=2,25. Die vergrößerte Eule hat einen Flächeninhalt von 2,25 m²
- Der Skalierungsfaktor ist 2; 2²= 4; 0,6 ⋅ 4 = 2,4. Die Tischdecke hat einen Flächeninhalt von 2,4 m².
- Der Skalierungsfaktor ist 0,5. 0,5² = 0,25; 2000 ⋅ 0,25 = 500. Die Pizza hat eine Fläche von 500 cm².
3. So verändern sich Körper beim Vergrößern und Verkleinern
4: In der Tabelle kann man die Werte für zwei Verdopplungen ablesen (blaue Pfeile). Das Volumen wächst jeweils auf das Achtfache. Ebenso kann man die Werte für zwei Verdreifachungen ablesen(lila Pfeile). Das Volumen wächst jeweils auf das Siebenundzwanzigfache.
5. Für eine Verdopplung - also k = 2 ist der Faktor 2²=8. Für eine Verdreifachung - also k = 3 ist der Faktor 3³ = 27. Allgemein gilt: Skaliert man einen Würfel mit dem Faktor k, muss man das Volumen mit dem Faktor k³ multiplizieren. (Man sagt auch: Rauminhalte wachsen kubisch.)
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in den Kasten "Würfelwachstum 3" in deinem Begleitheft.
Ergänze den Lückentext. Prüfe das Ergebnis und übertrage die Lösung in die Box "So verändern sich Körper beim Skalieren" im Begleitheft.
- 0,5³= 0,125; 8⋅0,125= 1. Der Würfel hat ein Volumen von 1 cm³
- Der Skalierungsfaktor ist 5. 5³=125; 4 ⋅ 125= 500 Die größte Murmel wiegt 500 g.
- Skalierungsfaktor 2: 2³=8: 400 ⋅ 8=3200. Die Vase hat ein Volumen von 3200 ml = 3,2 l.
4. Längen, Flächen- und Rauminhalte beim Skalieren - vernetzte Aufgaben
Lies die Zusammenfassung und übertrage die fett gedruckten Worte in die Box "So verändern sich Längen, Flächeninhalte und Volumina beim Skalieren"
- Die Teetasse ist etwa zwei Drittel so groß wie Alice. Da die vergrößerte Teetasse 80 cm hoch ist, ist die Schauspielerin also ca. 1,20 m groß.
Der Bühnenbauer hat aus den gemessenen Seitenlängen des Schachbretts dessen Fläche berechnet. Diese beträgt 0,25 m², die Kosten für das kleine Brett betragen also 800 €:4 = 200 €. Diese Rechnung ist korrekt. Die Seitenlängen des vergrößerten Schachbretts sind 10mal so groß, also 5m. Auch diese Überlegung ist richtig. Allerdings verhundertfach sich die Fläche und damit auch die Kosten für das Brett. Diese betragen also 20000 Euro.Der Bühnenbauer hat die Kosten aber fälschlicherweise nur verzehnfacht.
Stellungnahme: Hier gibt es keine eindeutige Antwort. Einerseits sind 20000 Euro schon recht viel Geld. Andererseits ist eine Filmproduktion sehr teuer - der Betrag von 20000 Euro ist im Vergleich gering. Allerdings können auch viele solch "kleinerer" Beträge die Kosten für die Produktion in die Höhe schießen lassen.
Annahme: Das Becken wird bis 5 cm unterhalb des Randes gefüllt. Dann wären im kleinen Becken 81 l Wasser (60cm ⋅ 30cm ⋅45cm = 85000cm³ = 81000ml = 81l). In das vergrößerte Becken müsste man dann 81l⋅1000 = 81000 l füllen. Die Wasserfüllung hat dann (unter normalen Bedingungen ein Gewicht von 81000 kg = 81 Tonnen. Schwieriger ist es, das Gewicht des Aquariums abzuschätzen, weil wir nicht wissen, ob
- das gleiche Material verwendet wird und
- die Glasdicke der Seiten ebenfalls verzehnfacht wird.
Setzt man beides voraus, wächst das Gewicht des Aquariums ebenfalls mit dem Faktor 1000 (die Seitenflächen sind als Körper zu betrachten). Das Aquarium würde also 12000 kg = 12 t wiegen. Insgesamt würde das gefüllte Aquarium also 93 t wiegen und die Traglast des Podestes wäre groß genug (auch für die Schauspielerin und eventuell Personen aus dem Filmteam samt Ausrüstung). Es bleiben jedoch Unsicherheiten:
- Laut unsere Annahme wurde es ja nur bis 50 cm unterhalb des Randes gefüllt. Würde das Becken bis zum Rand gefüllt, wären dies noch 9000 l Wasser, also 9 Tonnen zusätzlich. Dann wäre die Traglast des Podestes überschritten.
- Sollte das große Aquarium am Boden mit Steinen (statt Kies) gefüllt werden, würde das Aquarium schwerer werden. Nimmt man beispielsweise an, dass die unteren 50 cm (5 cm im Original) des Beckens mit Steinen gefüllt würden, würde sich das Gewicht um 18 Tonnen erhöhen (Faustformel: Steine wiegen etwa dreimal so viel wie Wasser.). Hier wäre die Traglast deutlich überschritten.