Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum: Unterschied zwischen den Versionen
(Unterseite angelegt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (118 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
{{Navigation|[[Benutzer:Buss-Haskert/Exponentialfunktion|Vorwissen]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum| 1) Lineares und exponentielles Wachstum (Einstieg)]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum|2) Wachstumsrate und Wachstumsfaktor ]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum|3) Exponentielles Wachstum]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion|4) Die Exponentialfunktion]]}} | |||
<br> | |||
==3 Exponentielles Wachstum== | ==3 Exponentielles Wachstum== | ||
{{Box|1=Einstieg: Weltbevölkerung|2=[[Datei:Person-2829500 1920.png|rechts|rahmenlos]]Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%. <br>Also gilt q=100%+1,25% = 101,25% = 1,0125<br> | {{Box|1=Einstieg: Weltbevölkerung|2=[[Datei:Person-2829500 1920.png|rechts|rahmenlos]]Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%. <br>Also gilt q=100%+1,25% = 101,25% = 1,0125<br> | ||
| Zeile 5: | Zeile 10: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
{{Lösung versteckt|[[Datei:Weltbevölkerung | {{Lösung versteckt|[[Datei:Weltbevölkerung Wertetabelle neu.png|rahmenlos|600x600px]]|Tipp zur Wertetabelle|Verbergen}} | ||
{{Lösung versteckt|1=Prognose für das Jahr 2030: n = 11<br> | {{Lösung versteckt|1=Prognose für das Jahr 2030: n = 11<br> | ||
W<sub>11</sub> = W<sub>0</sub> ∙ q<sup>11</sup><br> | W<sub>11</sub> = W<sub>0</sub> ∙ q<sup>11</sup><br> | ||
| Zeile 16: | Zeile 21: | ||
Die neue Größe nach n Zeitspannen berechnen wir mit<br> | Die neue Größe nach n Zeitspannen berechnen wir mit<br> | ||
'''<big>W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup></big>''', <br> | '''<big>W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup></big>''', <br> | ||
wobei q der Wachstumsfaktor ist. q = 1+p% | wobei q der Wachstumsfaktor ist. <br> | ||
<div class="grid"> | |||
<div class="width-1-2">Zunahme: q = 1 + p%, also q > 1</div> | |||
<div class="width-1-2">Abnahme: q = 1 - p%, also q < 1</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
<br> | <br> | ||
Die Gleichung W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> heißt <u>Exponentialgleichung</u>, da die Variable n im Exponenten steht. | Die Gleichung W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> heißt <u>Exponentialgleichung</u>, da die Variable n im Exponenten steht. | ||
{{Lösung versteckt|1=Erinnerung vermehrter/verminderter Grundwert in der Prozentrechnung:<br> | |||
vermehrter Grundert: G<sup>+</sup> = G · p<sup>+</sup>% (mit p<sup>+</sup>% = 1+p% = q)<br> | |||
verminderter Grundwert: G<sup>-</sup> = G · p<sup>-</sup>% (mit p<sup>-</sup>% = 1-p% = q)<br>|2=Zusammenhang Prozentrechnung|3=Verbergen}} | |||
<ggb_applet id="jtgzqdtf" width="1138" height="787" border="888888" /> | |||
Applet von C. Buß-Haskert Originallink https://www.geogebra.org/m/jtgzqdtf | |||
{{LearningApp|app=17257009|width=100%|heigth=600px}} | {{LearningApp|app=17257009|width=100%|heigth=600px}} | ||
{{LearningApp|app= | {{LearningApp|app=p62i35bq221|width=100%|heigth=600px}} | ||
{{LearningApp|app=17256599|width=100%|heigth=600px}} | {{LearningApp|app=17256599|width=100%|heigth=600px}} | ||
{{Box|Anwendungsaufgabe 1: | ==3.1 Exponentielles Wachstum: Beispiele und Anwendungen== | ||
{{ | ===3.1.1 W<sub>n</sub> gesucht=== | ||
{{Box|Anwendungsaufgabe 1: Bevölkerungswachstum (W<sub>n</sub> gesucht)|Die Bevölkerung in Indien beträgt zur Zeit 1,38 Milliarden Einwohner (2020). Die jährliche Zunahme beträgt derzeit 0,8%. <br> | |||
Wie viele Einwohner hat Indien im Jahr 2025?|Üben}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 1,38 Mrd.; p% = 0,8% = 0,008, also ist q = 1+0,008 = 1,008; n = 5 (von 2020 - 2025)<br> | |||
ges: W<sub>5</sub><br> | |||
<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup><br> | |||
W<sub>5</sub> = 1,38 · 1,008<sup>5</sup><br> | |||
= 1,436<br> | |||
Indien wird im Jahr 2025 ca. 1,436 Mrd. Einwohner haben.|2=Musterlösung|3=Verbergen}} | |||
{{Lösung versteckt|1=Du nutzt folgende Taste beim Taschenrechner, um Exponenten größer als 3 einzugeben (hier z.B. n = 8):<br> | |||
[[Datei:Taschenrechner Exponent eingeben markiert.png|rahmenlos|565x565px]]|2=Tipp zur Eingabe von Exponenten (Hochzahlen) in den Taschenrechner|3=Verbergen}} | |||
{{#ev:youtube|5daf0ozfr3o|800|center|||start=0&end=115}} | |||
<br> | |||
{{Box|Übung 1: Aufgabenfuchs|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/potenz/exp_wachstum.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. | |||
* 9 | |||
* 10 | |||
* 11 | |||
* 12 | |||
* 17 | |||
* 18 | |||
* 19 | |||
* 20 | |||
* 21|Üben}} | |||
<br> | |||
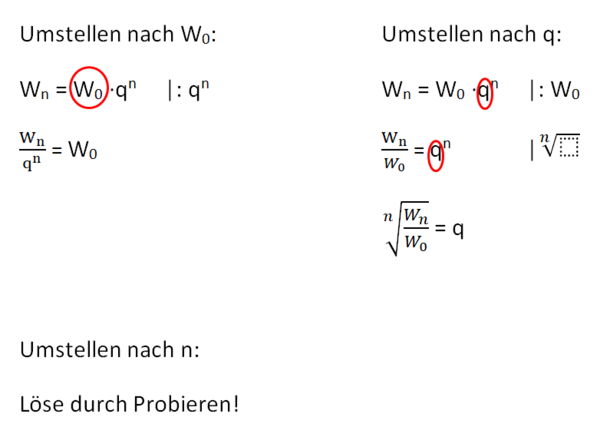
{{Box|Exponentialgleichung - Formel umstellen|[[Datei:Umstellen der Exponentialgleichung.png|rahmenlos|600x600px]]|Arbeitsmethode}} | {{Box|Exponentialgleichung - Formel umstellen|[[Datei:Umstellen der Exponentialgleichung.png|rahmenlos|600x600px]]|Arbeitsmethode}} | ||
{{Lösung versteckt|1=Du kannst die Formel auch nach n umstellen. Die Lösung erfolgt durch Logarithmieren. Eine Erklärung hierzu, findest du unten auf der Seite.|2=Hinweis zur Berechnung von n (Logarithmieren)|3=Verbergen}} | |||
{{Box|Anwendungsaufgabe | ===3.1.2 W<sub>0</sub> gesucht=== | ||
{{ | {{Box|Anwendungsaufgabe 2: Klimawandel (W<sub>0</sub> gesucht)|[[Datei:Iceberg-g3d68c08ff 1920.jpg|rechts|rahmenlos|100x100px]]Im Jahr 2021 ist die Fläche der Arktis mit 4,7 Mio km² deutlich kleiner als noch vor rund 30 Jahren. Die Abnahme beträgt mit leichten Schwankungen jährlich ca. 1,7%.<br> | ||
Wie groß war die Fläche vor 30 Jahren?|Üben}} | |||
{{Lösung versteckt|1=geg: W<sub>30</sub> = 4,7 Mio km²; p% = -1,7% = -0,017, also ist q = 1-0,017 = 0,983; n = 30 <br> | |||
ges: W<sub>0</sub><br> | |||
<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> | : q<sup>n</sup><br> | |||
W<sub>0</sub> = <math>\tfrac{W_n}{q^n}</math><br> | |||
W<sub>0</sub> = <math>\tfrac{W_{30}}{q^{30}}</math><br> | |||
= <math>\tfrac{4,7}{0,983^{30}}</math><br> | |||
≈ 7,86<br> | |||
Vor 30 Jahren betrug die Fläche der Arktis noch ca. 7,86 Mio km².|2=Musterlösung|3=Verbergen}} | |||
{{#ev:youtube|5u28338-gfc|800|center|||start=23&end=111}} | |||
{{Box|Übung 2: Aufgabenfuchs|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/potenz/exp_wachstum.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. | |||
* 22 | |||
* 23 | |||
* 24 | |||
* 25|Üben}} | |||
*Formel | ===3.1.3 q bzw. p% gesucht=== | ||
* | {{Box|Anwendungsaufgabe 3: Mietpreissteigerung (q und p% gesucht)|[[Datei:House-g7ece683db 1280.png|rechts|rahmenlos|100x100px]]Die Miete für eine Wohnung stieg innerhalb von 5 Jahren von 600€ auf 730€.<br> | ||
< | Um wie viel Prozent ist die Miete durchschnittlich pro Jahr gestiegen? |Üben}} | ||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 600 €; W<sub>5</sub> = 730 €; n = 5 <br> | |||
ges: q bzw. p%<br> | |||
<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> | : W<sub>0</sub><br> | |||
<math>\tfrac{W_n}{W_0}</math> = q<sup>n</sup> | <math>\sqrt[n]{}</math><br> | |||
<math>\sqrt[n]{\tfrac{W_n}{W_0}}</math> = q<br> | |||
<math>\sqrt[5]{\tfrac{730}{600}}= q</math><br> | |||
1,04 ≈ q<br> | |||
p% = q - 1 = 0,04 = 4% | |||
Die Mietsteigerung betrug jährlich 4%.|2=Musterlösung|3=Verbergen}} | |||
{{Lösung versteckt|Die n-te Wurzel bestimmst du mit dem Taschenrechner mit der Tastenkombination im Bild<br> | |||
[[Datei:Taschenrechner Bild n-te Wurzel.png|rahmenlos]]|Tipp: n-te Wurzel in den Taschenrechner eingeben|Verbergen}} | |||
<br> | |||
{{#ev:youtube|0Wf4oYr0ZnY|800|center|||start=23&end=122}} | |||
{{Box|Übung 3: Aufgabenfuchs|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/potenz/exp_wachstum.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. | |||
* 26 | |||
* 27 | |||
* 28 | |||
* 29 | |||
* 30|Üben}} | |||
<br> | |||
===3.1.4 n gesucht=== | |||
{{Box|Anwendungsaufgabe 4: Temperaturabnahme (n gesucht)|[[Datei:Tea-pot-gc1ced1e73 1280.png|rechts|rahmenlos|100x100px]]Eine Tasse Tee wird mit kochendem Wasser (100°C) aufgegossen. Die Temperatur sinkt jede Minute um 5%. Es wird empfohlen, Getränke nicht heißer als 65°C zu trinken. <br> | |||
Nach wie vielen Minuten ist der Tee kalt genug? |Üben}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 100°C; W<sub>n</sub> = 65°C ; p% = -5% = -0,05, also q = 1-0,05 = 0,95 <br> | |||
ges: n<br> | |||
<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> | |||
65 = 100 · 0,95<sup>n</sup> |:100<br> | |||
0,65 = 0,95<sup>n</sup> |Setze für n verschiedene Werte ein<br><br> | |||
Für n = 1 gilt: 0,95<sup>1</sup> = 0,95 > 0,65 <br> | |||
...<br> | |||
Für n = 8 gilt: 0,95<sup>8</sup> ≈ 0,66 '''>''' 0,65 <br> | |||
Für n = 9 gilt: 0,95<sup>9</sup> ≈ 0,63 '''<''' 0,65 <br> | |||
Also ist der Tee nach ca. 9 Minuten auf unter 65°C abgekühlt.<br> | |||
<br> | |||
Alternativ kannst du das Probieren auch in einer Wertetabelle notieren:<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} n (Zeit in Minuten) | |||
{{!}} 1 | |||
{{!}}... | |||
{{!}}8 | |||
{{!}}9 | |||
{{!}}... | |||
{{!-}} | |||
{{!}} W<sub>n</sub> (Temperatur in °C) | |||
W<sub>n</sub> = W<sub>0</sub>·q<sup>n</sup> | |||
{{!}} 95 | |||
{{!}}... | |||
{{!}} 66 | |||
{{!}} 63 | |||
{{!}}... | |||
{{!)}} | |||
<br> | |||
|2=Lösen durch Probieren|3=Verbergen}} | |||
{{Lösung versteckt|1=Du kannst die Lösung auch durch Logarithmieren lösen:<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup> <br> | |||
65 = 100 · 0,95<sup>n</sup> |:100<br> | |||
0,65 = 0,95<sup>n</sup> |log<br> | |||
log<sub>0,95</sub>0,65 = n<br> | |||
8,4 ≈ n<br> | |||
Also ist der Tee nach ca. 9 Minuten auf unter 65°C abgekühlt.|2=Lösen mit Logarithmieren|3=Verbergen}} | |||
{{Box|Übung 4: Aufgabenfuchs|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/potenz/exp_wachstum.shtml '''Aufgabenfuchs'''] die folgenden Aufgaben. | |||
* 37 | |||
* 38 | |||
* 39 | |||
* 40 | |||
* 41|Üben}} | |||
<br> | |||
{{Box|Übung 5|Löse die Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung. | |||
* S. 73 Nr. 1 | |||
* S. 73 Nr. 2 | |||
* S. 73 Nr. 4 | |||
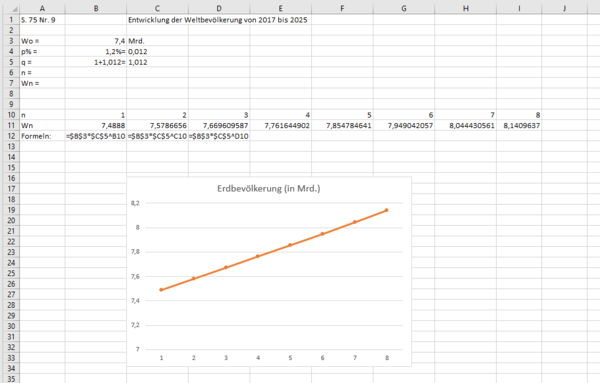
* S. 75 Nr. 9 | |||
* S. 75 Nr. 11 | |||
* S. 80 Nr. 7|Üben}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3<br> | |||
ges: W<sub>1</sub>; W<sub>2</sub>; ...; W<sub>5</sub><br> | |||
Rechne wie in Anwendungsaufgabe 1.|2=Tipp zu Nr. 1a|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3; W<sub>n</sub> = 1200 g<br> | |||
ges: n <br> | |||
Rechne wie in Anwendungsaufgabe 4. Löse durch systematische Probieren.<br> | |||
Lösung: | |||
für n = 6 ist W<sub>6</sub> = ... ≈965,4 g<br> | |||
für n = 7 ist W<sub>7</sub> = ... ≈ 1254,9 g<br> | |||
Nach etwas weniger als 7 Tagen ist die Algenmasse auf 1200 g gewachsen.<br> | |||
|2=Tipp zu Nr. 1b|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 18700 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009; n = 2 (von 2013 bis 2015)<br> | |||
ges: W<sub>2</sub><br> | |||
Rechne wie in Anwendungsaufgabe 1.|2=Tipp zu Nr. 2a|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>2</sub> = 22500 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009<br> | |||
ges: W<sub>0</sub> (2013) und W<sub>1</sub> (2014) <br> | |||
Rechne wie in Anwendungsaufgabe 2.|2=Tipp zu Nr. 2b|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 26200 €(im Jahr 2018); p% = 2,3% = 0,023, also q = 1+0,023 = 1,023; n = 5 (von 2018 bis 2023)<br> | |||
ges: W<sub>5</sub><br> | |||
Rechne wie in Anwendungsaufgabe 1.|2=Tipp zu Nr. 2c|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = ... (Bevölkerungszahlen im Jahr 2010); p% = 1,2% = 0,012, also q = 1+0,012= 1,012 usw.; n = 40 (von 2010 bis 2050)<br> | |||
ges: W<sub>40</sub> <br> | |||
Rechne jeweils wie in Anwendungsaufgabe 1.|2=Tipp zu Nr. 4a|3=Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP 10 S.75 Nr.9 Lösung.png|rahmenlos|600x600px]]|Tipp zu Nr. 9|Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 100% (Lichtintensität); p% = -11% = -0,11, also q = 1-0,11 = 0,89; n = 10 (in 10m Tiefe)<br> | |||
ges: W<sub>10</sub><br> | |||
Rechne wie in Anwendungsaufgabe 1.<br> | |||
Lösung: W<sub>10</sub> = ... ≈ 31,2%<br> | |||
In 10m Tiefe beträgt die Lichtintensität nur noch 31,2%. |2=Tipp zu Nr. 11|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: Luftdruck in Meereshöhe W<sub>0</sub>=1013 hPa; Abnahme je 100m p%=-1,23%=-0,0123, also q=1-0,0123 = 0,9877; Höhe des Kilimandscharo 5895m = 58,95· 100 m, also x = 58,95 und des Mt. Everest 8848m = 88,48·100 m, also x = 88,48<br> | |||
ges: Luftdruck auf den Bergen, also W<sub>x</sub><br> | |||
W<sub>x</sub> = W<sub>0</sub> · q<sup>x</sup><br> | |||
= 1013 · 0,9877<sup>58,95</sup><br> | |||
≈ 488,4 (hPa) <br> | |||
Rechne ebenso für den Mt Everest (Lösung: 338,9 hPa)|2=Tipp zu Nr. 7a|3=Verbergen}} | |||
{{Lösung versteckt|1=Bestimme zunächst den Luftdruck in 500 m Höhe (also x = 5) und in 841 m Höhe (also x = 8,41). Danach berechne den Unterschied von beiden. dies ist W.<br> | |||
Den prozentuale Unterschied berechne mit p% = <math>\tfrac{W}{G}</math>, mit dem Grundwert in 500m Höhe.|2=Tipp zu Nr. 7b|3=Verbergen}} | |||
{{Lösung versteckt|1=Gib die Funktionsgleichung bei GeoGebra ein. W<sub>x</sub> = 1013 · 0,9887<sup>x:100</sup> <br> | |||
x steht hier für die Höhe, in der der Luftdruck berechnet werden soll.<br> | |||
[[Datei:SP10 S.80 Nr7c.png|rahmenlos|600x600px]]|2=Tipp zu Nr. 7c|3=Verbergen}} | |||
<br> | |||
{{Box|Übung 6: Aufgabenfuchs|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/potenz/exp_wachstum.shtml '''Aufgabenfuchs'''] die vermischten Aufgaben. | |||
* 31 | |||
* 32 | |||
* 33 | |||
* 34 | |||
* 35 | |||
* 36|Üben}} | |||
<br> | |||
{{Box|Übung 7: ANTON-APP|Bearbeite die Übungen zum exponentiellen Wachstum in der [https://anton.app/de/ ANTON-App].|Üben}} | |||
<br> | |||
==3.2 Anwendung des exponentiellen Wachstums: Zinseszinsrechnung== | |||
{{Box|1=Zinseszins|2=Zinseszins bedeutet, dass ein Startkapital Zinsen erwirtschaftet und diese Zinsen werden dem Vermögen am Jahresende gutgeschrieben. So werden in Zukunft diese Zinsen ebenfalls verzinst.<br> | |||
Das Kapital nach n Jahren wird mit der Formel <br> | |||
'''<big>K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup> mit q = 1 + p%'''</big>'''<br> | |||
|3=Arbeitsmethode}} | |||
Bei diesem Kapitalwachstum handelt es sich um ein exponentielles Wachstum. | |||
<br> | |||
{{Box|1=Übung 8 (online)|2=Löse auf der Seite [https://mathe.aufgabenfuchs.de/zins/zinseszins.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 1 (Hier kannst du z.B. das Einstiegsbeispiel einstellen) | |||
* 2 (Nutze die Zinseszinsformel K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup>) | |||
* 3 (Nutze die Zinseszinsformel K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup>)|3=Üben}} | |||
{{Box|Übung 9|[[Datei:Business-g97f006239 1280.png|rechts|rahmenlos|200x200px]]a) Ein Kapital von 2000€ wird zu einem Zinssatz von 2% angelegt. Berechne das Kapital nach 4 Jahren.<br> | |||
b) Ein Vermögen von 7500€ wird zu einem Zinssatz von 1,5% angelegt (mit Zinseszins). Berechne das Kapital nach 5 Jahren.|Üben}} | |||
{{Lösung versteckt|Vergleiche deine Lösung mit dem Beispiel a) auf S. 73 oben.|Tipp zu a)|Verbergen}} | |||
{{Lösung versteckt|1=geg:K = 7500€; p% = 1,5% = 0,015, also q = 1 + 0,015 =1,015; n = 5<br> | |||
K<sub>5</sub> = K<sub>0</sub> ∙ q<sup>5</sup> <br> | |||
= 7500 ∙ 1,015<sup>5</sup><br> | |||
= 8079,63 (€)|2=Tipp zu b)|3=Verbergen}} | |||
{{Box|1=Umstellen der Zinseszinformel|2=<div class="grid"> | |||
<div class="width-1-2"><big> Formel umstellen nach K<sub>0</sub></big><br> ("Wie hoch war das Startkapital...?):<br> | |||
K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup> |:q<sup>n</sup><br> | |||
<math>\tfrac{K_n}{q^n}</math>= K<sub>0</sub><br> | |||
<br> | |||
<br></div> | |||
<div class="width-1-2"><big>Formel umstellen nach q </big><br>("Mit welchem Prozentsatz ...?):<br> | |||
K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup> |:K<sub>0</sub><br> | |||
<math>\tfrac{K_n}{K^0}</math> = q<sup>n</sup> |<math>\sqrt[n]{}</math><br> | |||
<math>\sqrt[n]{\tfrac{K_n}{K_0}}</math> = q<br> | |||
Bestimme dann p% mit q = 1+p%, <br>also q-1 = p%.<br> | |||
<br></div> | |||
</div> | |||
<big>Formel umstellen nach n </big><br>("Nach wie vielen Jahren...?"):<br><br> | |||
Löse hier also durch systematisches '''Probieren'''!<br> | |||
Setze für n verschiedene Zahlen ein und teste, für welchen Wert von n die Gleichung erfüllt wird. | |||
(Das Umstellen der Formel nach n erfordert die Anwendung des Logarithmus. Du darfst auch durch Logarithmieren lösen.) <br> | |||
<br><br>|3=Arbeitsmethode}} | |||
{{Box|Hefteintrag: Beispiele|Übertrage die Beispielaufgaben und die Lösungen aus dem Video in dein Heft. Starte das Video und stoppe es nach jedem Beispiel a), b) und c). Notiere vollständig und übersichtlich in deinem Heft.|Arbeitsmethode}} | |||
{{#ev:youtube|QnerUmGTvJo|800|center|||start=193&end=420}} | |||
{{Box|Übung 10 (online)|Wähle aus den folgenden Aufgaben '''mindestens zwei''' Aufgaben aus und löse: Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/zins/zinseszins.shtml '''Aufgabenfuchs'''] | |||
* 5 | |||
* 6 | |||
* 7 | |||
* 8 | |||
* 9|Üben}} | |||
{{Box|Übung 11 - Zinseszinsrechnung|Löse die Aufgabe aus dem Buch. Notiere die gegebenen und gesuchten Größen, stelle die Formel für die Zinsrechnung nach der gesuchten Größe um und berechne. | |||
* S. 73 Nr. 3|Üben}} | |||
{{Lösung versteckt|1=a) geg:...<br> | |||
ges: q; K<sub>n</sub><br> | |||
q = 1 + p% = 1 + 0,015 = 1,015<br> | |||
K<sub>5</sub> = K<sub>0</sub> ∙ q<sup>5</sup> Setze die Werte ein und berechne mit dem Taschenrechner.|2=Tipp zu Nr. 3a|3=Verbergen}} | |||
{{Lösung versteckt|1=b) geg:...<br> | |||
ges: p%; K<sub>n</sub><br> | |||
p% = q - 1 = 1,035 - 1 = 0,035 = 3,5%<br> | |||
Berechne K<sub>n</sub> durch einsetzen der Werte in die Formel.|2=Tipp zu Nr. 3b|3=Verbergen}} | |||
{{Lösung versteckt|1=c) geg: ...<br> | |||
ges: K<sub>0</sub>; p%<br> | |||
Stelle die Formel nach K<sub>0</sub> um und setze dann die gegebenen Werte ein.|2=Tipp zu Nr. 3c|3=Verbergen}} | |||
{{Lösung versteckt|1=d)geg: ...<br> | |||
ges: q und p%<br> | |||
Stelle die Formel nach q um und setzte die gegebene Größen ein. Bestimme so den Wert für q.<br> | |||
Berechne dann p% mit p% = q-1 (Wandel den Dezimalbruch in Prozent um.)|2=Tipp zu Nr. 3d|3=Verbergen}} | |||
{{Lösung versteckt|1=e) geg: ...<br> | |||
ges: q; n<br> | |||
q = 1 + p% = ...<br> | |||
Bestimme n durch Probieren.<br> | |||
Setze für n die Zahlen 1, 2, 3, ... ein und prüfe, für welchen Wert von n die Gleichung eine wahre Aussage ergibt.|2=Tipp zu Nr. 3e|3=Verbergen}} | |||
{{Lösung versteckt|1=e) geg: K<sub>0</sub> = 2500€; K<sub>n</sub> = 3359,79€; p% = 3% = 0,03<br> | |||
ges: q; n<br> | |||
q = 1 + p% = 1 + 0,03 = 1,03<br> | |||
K<sub>n</sub> = K<sub>0</sub> ·q<sup>n</sup> |Werte einsetzen<br> | |||
3359,79 = 2500 ·1,03<sup>n</sup> |:2500<br> | |||
1,34 ≈ 1,03<sup>n</sup><br> | |||
Setze verschiedene Werte für n ein und vergleiche den Wert im Taschenrechner mit 1,34:<br> | |||
n = 9: 1,03<sup>9</sup> ≈ 1,304 < 1,34<br> | |||
n = 10: 1,03<sup>10</sup> ≈ 1,34 = 1,34<br> | |||
Also n = 10 (Jahre).|2=Lösung zu Nr. 3e (Probieren)|3=Verbergen}} | |||
{{#ev:youtube|dV4Z13x9pJo|800|center}} | |||
{{#ev:youtube|KNHx5kpGbjY|800|center}} | |||
{{#ev:youtube|qyVqgnueWvg|800|center}} | |||
{{Box|Übung 12 - Anwendungsaufgaben zur Zinseszinsrechnung|Löse die Aufgaben aus dem Buch. Notiere die gegebenen und gesuchten Größen, stelle die Formel für die Zinsrechnung nach der gesuchten Größe um und berechne. | |||
* S. 73 Nr. 5a (**) | |||
* S. 75 Nr. 8 (Nutze GeoGeogebra) | |||
* S. 79 Nr. 1 | |||
* S. 83 Nr. 10 | |||
* S. 87 Nr. 6 (links) | |||
* S. 87 Nr. 7 (links) | |||
|Üben}} | |||
{{Lösung versteckt|1=Rechne zunächst mit einem Betrag von z.B. K<sub>0</sub> = 1000€<br> | |||
geg: K<sub>0</sub> = 1000€; K<sub>n</sub> = 2 ∙ 1000€ = 2000€; p% = 1,8% = 0,018, q = 1 + 0,018 = 1,018<br> | |||
Löse durch Probieren, für welchen Wert die Zinseszinsformel eine wahre Aussage ergibt oder K<sub>n</sub> mehr als 2000€ beträgt.|2=Tipp zu Nr. 5a|3=Verbergen}} | |||
{{Lösung versteckt|1=Stelle die passende Gleichung auf und gib diese bei GeoGebra ein. Löse damit Aufgabenteil c) und d),<br> | |||
K<sub>n</sub>=7200∙1,018<sup>n</sup><br> | |||
Funktionsgleichung: f(x) = 7200∙1,018<sup>x</sup><br>|2=Tipp zu Nr. 8|3=Verbergen}} | |||
{{Lösung versteckt|1=Vergleiche die beiden Angebote:<br> | |||
Angebot A: <br> | |||
geg: K<sub>0</sub> = 10000€; p% = 2,25% = 0,0225, also q = 1,0225; n = 7 Jahre<br> | |||
ges: K<sub>n</sub><br> | |||
K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup> Setze ein und berechne.<br> | |||
<br> | |||
Angebot B:<br> | |||
geg: K<sub>0</sub> = 10000€; p% = 1,5% = 0,015, also q = 1,015; n = 7 Jahre; auf das Kapital nach 7 Jahren K<sub>7</sub> gibt es zusätzlich 10%.<br> | |||
K<sub>n</sub> = K<sub>0</sub> ∙ q<sup>n</sup> Setze ein und berechne.<br> | |||
Berechne dann das Endkapital, indem du auf K<sub>7</sub> noch einmal einen Aufschlag von 10% rechnest:<br> | |||
Endkapital K<sub>Ende</sub> = K<sub>7</sub> ∙ 1,1 ...<br> | |||
denn p% = 10% = 0,1, also gilt q = 1,1.|2=Tipp zu Nr. 1|3=Verbergen}} | |||
{{Lösung versteckt|1=a) geg: K<sub>0</sub> = 2800€; n = 5; K<sub>5</sub> = 3607,75€;<br> | |||
ges: Zinssatz p% (Berechne zunächst q und damit dann p%).<br> | |||
b) K<sub>0</sub> = 5000€; p% = 4,5 = 0,045, also q = 1,045; K<sub>n</sub> = 2 ∙ 5000€ = 10000€ ("verdoppelt")<br> | |||
ges: n <br> | |||
Löse durch Probieren!<br> | |||
c) geg: n = 8 Jahre; p% = 5,25% = 0,0525, also q = 1 + 0,0525 = 1,0525; K<sub>8</sub> = 6776,25€<br> | |||
ges: K<sub>0</sub><br> | |||
Stelle die Zinseszinsformel nach K<sub>0</sub> um und setzte die gegebenen Werte ein.|2=Tipp zu Nr. 10|3=Verbergen}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit denen hinten im Buch. (Rückspiegelaufgaben)|Tipp zu Nr. 6 und 7|Verbergen}} | |||
{{Lösung versteckt|1=Vergleiche deine Lösungen zu den Aufgaben oben (bunte Mischung)<br> | |||
K<sub>0</sub> = 500€; K<sub>0</sub> = 4500€<br> | |||
p% = 1,2%; p% = 1%; p% = 3,5%; p% = 5,2%; <br> | |||
q=1,015; q = 1,01; q =1,03<br> | |||
K<sub>n</sub>=8079,63€; K<sub>n</sub> = 11685,39€; K<sub>n</sub> = 11098,45€; K<sub>n</sub> = 12208,29€<br> | |||
n = 10 Jahre; n = 39 Jahre; n = 16 Jahre|2=Vergleiche deine Lösungen zu den Aufgaben (Übung 12)|3=Verbergen}} | |||
==3.3 Anwendung des exponentiellen Wachstums: Halbwertszeit und Generationszeit (Verdopplungszeit)== | |||
Einstieg: evtl. Bierschaumzerfall (Untersuchtung auf [https://www.leifiphysik.de/kern-teilchenphysik/radioaktivitaet-einfuehrung/versuche/bierschaumzerfall leifiphysik]) | |||
{{Box|1=Halbwertszeit|2=Die Halbwertszeit T<sub><math>\tfrac{1}{2}</math></sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge radioaktiven Materials '''halbiert''' hat.<br> | |||
Der '''Wachstumsfaktor''' ist also '''q = '''100% - 50% = 1 - 0,5 = '''0,5''' und <br> | |||
die Anzahl '''n der Zerfallsprozesse''' wird berechnet mit n = <math>\tfrac{Zeit}{Halbwertszeit}</math>.|3=Kurzinfo}} | |||
Das nachfolgende Applet stellt den Zerfallsprozess anschaulich dar: | |||
*Halbwertszeit (Atome) | *Halbwertszeit (Atome) | ||
Direkter Link: https://www.geogebra.org/m/cq62nsqj | |||
<ggb_applet id="fvudcjym" width="1100" height="650" border="888888" /> | <ggb_applet id="fvudcjym" width="1100" height="650" border="888888" /> | ||
Applet von Hegius, | <small>Applet von Hegius, Mathezone</small> | ||
{{Box|1=Generationszeit/ Verdopplungszeit|2= Die Generationszeit T<sub>2</sub> gibt an, nach welcher Zeitspanne sich die Ausgangsmenge / Population '''verdoppelt''' hat.<br> | |||
Der '''Wachstumsfaktor''' ist also '''q ='''100%+100% = 1 + 1 = '''2 '''und <br> | |||
die Anzahl n der Generationszeiten wird berechnet mit n = <math>\tfrac{Zeit}{Generationszeit}</math>.|3=Kurzinfo}} | |||
Das nachfolgende Applet stellt den Verdopplungsprozess anschaulich dar: | |||
*Generationszeit/ Verdopplungszeit (Bakterien) | |||
Direkter Link: passt das Applet?? | |||
<ggb_applet id="etu2dsm8" width="566" height="663" border="888888" /> | |||
<small>Applet von Hegius, R. Schürz</small> | |||
{{Box|Übung 13 - Halbwertszeit und Generationszeit(Verdopplungszeit)|Löse die Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung. | |||
* S. 75 Nr. 10 | |||
* S. 79 Nr. 4 | |||
* S. 79 Nr. 5 | |||
* S. 80 Nr. 8 | |||
* S. 80 Nr. 9 | |||
* S. 80 Nr. 10 | |||
* S. 83 Nr. 12 (**) | |||
* S. 85 Nr. 23 (***) | |||
* S. 85 Nr. 26 (**)|Üben}} | |||
{{Lösung versteckt|1=geg: Wismut 210 mit T<sub><math>\tfrac{1}{2}</math></sub> = 5 Tage; q = 0,5 und Ausgangsmenge W<sub>0</sub> = 100g.<br> | |||
Zeit = 30 Tage, in 5 Tagesabschnitten, also für n = 1, 2, 3, 4, 5 und 6<br> | |||
ges: Wertetabelle:<br> | |||
W<sub>1</sub> = W<sub>0</sub> · 0,5<sup>1</sup> <br> | |||
= 100 · 0,5 = 50 (g)<br> | |||
W<sub>2</sub> = W<sub>0</sub> · 0,5<sup>2</sup> <br> | |||
= 100 · 0,5<sup>2</sup> = 25 (g)<br> | |||
W<sub>3</sub> = W<sub>0</sub> · 0,5<sup>3</sup> <br> | |||
= 100 · 0,5<sup>3</sup> = 12,5 (g)<br> | |||
...<br> | |||
[[Datei:S.75 Nr.10a.png|rahmenlos|600x600px]]|2=Tipps zu Nr. 10a|3=Verbergen}} | |||
{{Lösung versteckt|1=Nach 2 Halbwertszeiten ist nur noch ein Viertel der ursprünglichen Menge vorhanden, also nach 2·5 = 10 Tagen.|2=Tipp zu Nr. 10b|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: Radium-229 mit T<sub><math>\tfrac{1}{2}</math></sub> = 240 s; q = 0,5 und Ausgangsmenge W<sub>0</sub> = 48g.<br> | |||
Zeit = 6 Minuten = 360 s<br> | |||
ges: n; W<sub>n</sub><br> | |||
n = <math>\tfrac{Zeit}{Halbwertszeit}</math> = <math>\tfrac{360}{240}</math> = 1,5<br> | |||
W<sub>1,5</sub> = 48 · 0,5<sup>1,5</sup> = ... | |||
|2=Tipp zu Nr. 4a|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: Radium-229 mit T<sub><math>\tfrac{1}{2}</math></sub> = 240 s; q = 0,5 und Ausgangsmenge W<sub>0</sub> = 48mg.<br> | |||
W<sub>n</sub> = 1,5 mg <br> | |||
ges: n; t (Zeit)<br> | |||
<br> | |||
1,5 = 48 · 0,5<sup>n</sup><br> | |||
Löse durch systematisches Probieren.<br> | |||
Lösung: n = 5, also t = 5·240 s = 1200 s = 20 min | |||
|2=Tipp zu Nr. 4b|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: Generationszeit T<sub>2</sub> = 45 Tage; W<sub>0</sub> = 10 (Ratten); q = 2; t = 3 Monate = 90 Tage; n = <math>\tfrac{t}{T_2}</math> = <math>\tfrac{90}{45}</math> = 2<br> | |||
ges: W<sub>n</sub><br>|2=Tipp zu Nr. 8a|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: Generationszeit T<sub>2</sub> = 45 Tage = 1,5 Monate; q = 2; W<sub>0</sub> = 10 (Ratten); W<sub>n</sub> = 80 Mio; <br> | |||
ges: n; t<br> | |||
Löse durch systematisches Probieren. (Lösung: n = 23; t = n·1,5 (Monate))|2=Tipp zu Nr. 8b|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: n = 23 (wie in Nr. 8b)<br> | |||
ges: t = n·2 (Monate)(Lösung: n = 23)|2=Tipp zu Nr. 8c|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: q = 2; W<sub>0</sub> = 50 Bakterien; T<sub>2</sub> = 30 Minuten = 0,5 Stunden; t= 3,5 Stunden; n = <math>\tfrac{t}{T_2}</math> = <math>\tfrac{3,5}{0,5}</math> = 7<br> | |||
ges: W<sub>n</sub>|2=Tipp zu Nr. 9|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: q = 2; T<sub>2</sub> = 3 Wochen; W<sub>n</sub> = 100·W<sub>0</sub><br> | |||
ges: n; t<br> | |||
W<sub>n</sub> = W<sub>0</sub>·q<sup>n</sup> | Setze q = 2 und W<sub>n</sub> = 100·W<sub>0</sub> ein <br> | |||
Löse durch systematisches Probieren.<br> | |||
(Lösung: n = 6,6 , also t = ...|2=Tipp zu Nr. 10|3=Verbergen}} | |||
{{Lösung versteckt|1=<div class="grid"> | |||
<div class="width-1-2">geg: W<sub>0</sub>= 400 (Bakterien); q = 2 ("verdoppeln"); T<sub>2</sub> = 18,8 min; T = 2 h<br> | |||
ges: n; W<sub>n</sub><br> | |||
n = <math>\tfrac{T}{T_2} = \tfrac{120}{18,8}</math> ≈ 6,4<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup><br> | |||
...</div> | |||
<div class="width-1-2">2. Möglichkeit: Berechne zunächst den Wachstumsfaktor für 1 Minute:<br> | |||
geg: W<sub>0</sub> = 400; W<sub>18,8</sub> = 2·400 = 800; n = 18,8<br> | |||
ges: q<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup><br> | |||
800 = 400 · q<sup>18,8</sup> |:400 | |||
2 = q<sup>18,8</sup> |<math>\sqrt[18,8]{...}</math><br> | |||
<math>\sqrt[18,8]{2}</math> = q<br> | |||
1,038 ≈ q<br> | |||
<br> | |||
geg: W<sub>0</sub> = 400; n = 2h = 120min; q = 1,038<br> | |||
ges: Wn<br> | |||
...</div> | |||
</div> | |||
|2=Tipp zu Nr. 12|3=Verbergen}} | |||
< | {{Lösung versteckt|1=geg: W<sub>0</sub> = 100% (die gesamte Menge des Stoffe ist noch da); W<sub>6</sub> = 100% - 34% = 66%; n = 6<br> | ||
ges: q<br> | |||
W<sub>6</sub> = W<sub>0</sub> · q<sup>6</sup> | Umstellen nach q <br> | |||
<math>\sqrt[6]{\tfrac{W_6}{W_0}}</math> = q<br> | |||
<math>\sqrt[6]{\tfrac{0,66}{1}}</math> = q <br> | |||
0,933 ≈ q<br> | |||
Nun berechne die Halbwertszeit:<br> | |||
geg: W<sub>0</sub> = 100%; W<sub>n</sub> = 50%; q = 0,933<br> | |||
ges: n<br> | |||
W<sub>n</sub> = W<sub>0</sub> · q<sup>n</sup><br> | |||
0,5 = 1 · 0,993<sup>n</sup> <br> Löse durch Probieren.<br> | |||
Für n = 9 gilt: W<sub>9</sub> ≈ 0,54<br> | |||
Für n = 10 gilt: W<sub>10</sub> ≈ 0,4998<br> | |||
Also beträgt die Halbwertszeit ca. 10 Jahre, denn nach 10 Jahren hat sich die Stoffmenge halbiert.|2=Lösung zu Nr. 23|3=Verbergen}} | |||
{{Lösung versteckt|1=geg: W<sub>0</sub> = 100%; W<sub>24</sub> = 300% (verdreifacht); n = 24 <br> | |||
ges: q (prozentuales Wachstum pro Tag); p%<br> | |||
...<br> | |||
Lösung: q=1,0468|2=Tipp zu Nr. 26a|3=Verbergen}} | |||
<br> | |||
==Einschub: Logarithmieren== | |||
Ist beim exponentiellen Wachstum der '''Exponent '''n '''gesucht''', kannst du diesen Wert durch systematisches Probieren erhalten. Eine genauere Möglichkeit ist das Logarithmieren.<br> | |||
{{Box|1=Definition Logarithmus|2=Als Logarithmus wird der Exponent n bezeichnet, mit dem man die Basis b potenziert, um die Zahl a zu erhalten (a und b positiv):<br> | |||
b<sup>n</sup>=a, dann gilt log<sub>b</sub>a = n<br> | |||
Beispiele: | |||
* log<sub>2</sub>8 = 3; denn 2<sup>3</sup> = 8<br> | |||
* log<sub>10</sub>100000 = 5; denn 10<sup>5</sup> = 100000 | |||
Für die Berechnung des Exponenten in den Aufgaben zum exponentiellen Wachstum nutzt du die folgende Tastenfolge:<br> | |||
5<sup>x</sup> = 25<br> | |||
x = log<sub>5</sub>25 <br> | |||
x = 2 (Zeigt dein Taschenrechner dann als Ergebnis an.) | |||
|3=Kurzinfo}}<br> | |||
{{Lösung versteckt|1=Falls du einen Taschenrechner nutzt, der diese Möglichkeit nicht hat, tippe wie folgt:<br> | |||
x = <math>\tfrac{log25}{log5}</math><br> | |||
x = 2|2=andere Möglichkeit: Taschenrechnereingabe|3=Verbergen}} | |||
{{#ev:youtube|f1tFVT0_Iz8|800|center}} | |||
< | {{Box|1=Übung zum Logarithmieren|2=Löse S. 84 Nr. 21b mithilfe des Taschenrechners:<br> | ||
3<sup>x</sup> = 50 also ist <br> | |||
x = log<sub>3</sub>50<br> | |||
x ≈ 3,56|3=Üben}} | |||
<br> | |||
{{Fortsetzung|weiter=4 Die Exponentialfunktion|weiterlink=Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion}} | |||
Aktuelle Version vom 12. Januar 2025, 16:54 Uhr
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
3 Exponentielles Wachstum
Prognose für das Jahr 2030: n = 11
W11 = W0 ∙ q11
= 7,70 ∙ 1,02511
Die Gleichung Wn = W0 · qn heißt Exponentialgleichung, da die Variable n im Exponenten steht.
Erinnerung vermehrter/verminderter Grundwert in der Prozentrechnung:
vermehrter Grundert: G+ = G · p+% (mit p+% = 1+p% = q)

Applet von C. Buß-Haskert Originallink https://www.geogebra.org/m/jtgzqdtf
3.1 Exponentielles Wachstum: Beispiele und Anwendungen
3.1.1 Wn gesucht
geg: W0 = 1,38 Mrd.; p% = 0,8% = 0,008, also ist q = 1+0,008 = 1,008; n = 5 (von 2020 - 2025)
ges: W5
Wn = W0 · qn
W5 = 1,38 · 1,0085
= 1,436
Du nutzt folgende Taste beim Taschenrechner, um Exponenten größer als 3 einzugeben (hier z.B. n = 8):

3.1.2 W0 gesucht
geg: W30 = 4,7 Mio km²; p% = -1,7% = -0,017, also ist q = 1-0,017 = 0,983; n = 30
ges: W0
Wn = W0 · qn | : qn
W0 =
W0 =
=
≈ 7,86
3.1.3 q bzw. p% gesucht
geg: W0 = 600 €; W5 = 730 €; n = 5
ges: q bzw. p%
Wn = W0 · qn | : W0
= qn |
= q
1,04 ≈ q
p% = q - 1 = 0,04 = 4%
3.1.4 n gesucht
geg: W0 = 100°C; Wn = 65°C ; p% = -5% = -0,05, also q = 1-0,05 = 0,95
ges: n
Wn = W0 · qn
65 = 100 · 0,95n |:100
0,65 = 0,95n |Setze für n verschiedene Werte ein
Für n = 1 gilt: 0,951 = 0,95 > 0,65
...
Für n = 8 gilt: 0,958 ≈ 0,66 > 0,65
Für n = 9 gilt: 0,959 ≈ 0,63 < 0,65
Also ist der Tee nach ca. 9 Minuten auf unter 65°C abgekühlt.
Alternativ kannst du das Probieren auch in einer Wertetabelle notieren:
| n (Zeit in Minuten) | 1 | ... | 8 | 9 | ... |
| Wn (Temperatur in °C)
Wn = W0·qn |
95 | ... | 66 | 63 | ... |
Du kannst die Lösung auch durch Logarithmieren lösen:
Wn = W0 · qn
65 = 100 · 0,95n |:100
0,65 = 0,95n |log
log0,950,65 = n
8,4 ≈ n
geg: W0 = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3
ges: W1; W2; ...; W5
geg: W0 = 200 g; p% = 30% = 0,3, also q = 1+0,3 = 1,3; Wn = 1200 g
ges: n
Rechne wie in Anwendungsaufgabe 4. Löse durch systematische Probieren.
Lösung:
für n = 6 ist W6 = ... ≈965,4 g
für n = 7 ist W7 = ... ≈ 1254,9 g
geg: W0 = 18700 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009; n = 2 (von 2013 bis 2015)
ges: W2
geg: W2 = 22500 €; p% = 0,9% = 0,009, also q = 1+0,009 = 1,009
ges: W0 (2013) und W1 (2014)
geg: W0 = 26200 €(im Jahr 2018); p% = 2,3% = 0,023, also q = 1+0,023 = 1,023; n = 5 (von 2018 bis 2023)
ges: W5
geg: W0 = ... (Bevölkerungszahlen im Jahr 2010); p% = 1,2% = 0,012, also q = 1+0,012= 1,012 usw.; n = 40 (von 2010 bis 2050)
ges: W40
geg: W0 = 100% (Lichtintensität); p% = -11% = -0,11, also q = 1-0,11 = 0,89; n = 10 (in 10m Tiefe)
ges: W10
Rechne wie in Anwendungsaufgabe 1.
Lösung: W10 = ... ≈ 31,2%
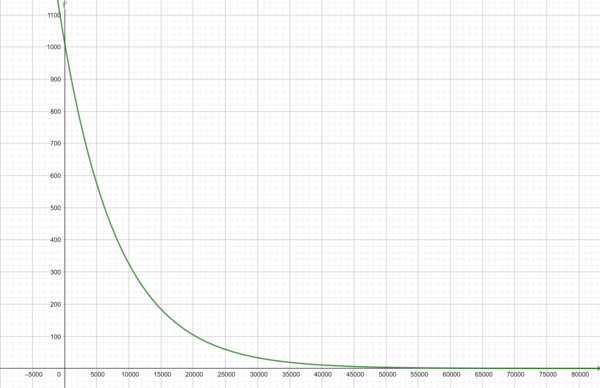
geg: Luftdruck in Meereshöhe W0=1013 hPa; Abnahme je 100m p%=-1,23%=-0,0123, also q=1-0,0123 = 0,9877; Höhe des Kilimandscharo 5895m = 58,95· 100 m, also x = 58,95 und des Mt. Everest 8848m = 88,48·100 m, also x = 88,48
ges: Luftdruck auf den Bergen, also Wx
Wx = W0 · qx
= 1013 · 0,987758,95
≈ 488,4 (hPa)
Bestimme zunächst den Luftdruck in 500 m Höhe (also x = 5) und in 841 m Höhe (also x = 8,41). Danach berechne den Unterschied von beiden. dies ist W.
Gib die Funktionsgleichung bei GeoGebra ein. Wx = 1013 · 0,9887x:100
x steht hier für die Höhe, in der der Luftdruck berechnet werden soll.
3.2 Anwendung des exponentiellen Wachstums: Zinseszinsrechnung
Bei diesem Kapitalwachstum handelt es sich um ein exponentielles Wachstum.
geg:K = 7500€; p% = 1,5% = 0,015, also q = 1 + 0,015 =1,015; n = 5
K5 = K0 ∙ q5
= 7500 ∙ 1,0155
a) geg:...
ges: q; Kn
q = 1 + p% = 1 + 0,015 = 1,015
b) geg:...
ges: p%; Kn
p% = q - 1 = 1,035 - 1 = 0,035 = 3,5%
c) geg: ...
ges: K0; p%
d)geg: ...
ges: q und p%
Stelle die Formel nach q um und setzte die gegebene Größen ein. Bestimme so den Wert für q.
e) geg: ...
ges: q; n
q = 1 + p% = ...
Bestimme n durch Probieren.
e) geg: K0 = 2500€; Kn = 3359,79€; p% = 3% = 0,03
ges: q; n
q = 1 + p% = 1 + 0,03 = 1,03
Kn = K0 ·qn |Werte einsetzen
3359,79 = 2500 ·1,03n |:2500
1,34 ≈ 1,03n
Setze verschiedene Werte für n ein und vergleiche den Wert im Taschenrechner mit 1,34:
n = 9: 1,039 ≈ 1,304 < 1,34
n = 10: 1,0310 ≈ 1,34 = 1,34
Rechne zunächst mit einem Betrag von z.B. K0 = 1000€
geg: K0 = 1000€; Kn = 2 ∙ 1000€ = 2000€; p% = 1,8% = 0,018, q = 1 + 0,018 = 1,018
Stelle die passende Gleichung auf und gib diese bei GeoGebra ein. Löse damit Aufgabenteil c) und d),
Kn=7200∙1,018n
Vergleiche die beiden Angebote:
Angebot A:
geg: K0 = 10000€; p% = 2,25% = 0,0225, also q = 1,0225; n = 7 Jahre
ges: Kn
Kn = K0 ∙ qn Setze ein und berechne.
Angebot B:
geg: K0 = 10000€; p% = 1,5% = 0,015, also q = 1,015; n = 7 Jahre; auf das Kapital nach 7 Jahren K7 gibt es zusätzlich 10%.
Kn = K0 ∙ qn Setze ein und berechne.
Berechne dann das Endkapital, indem du auf K7 noch einmal einen Aufschlag von 10% rechnest:
Endkapital KEnde = K7 ∙ 1,1 ...
a) geg: K0 = 2800€; n = 5; K5 = 3607,75€;
ges: Zinssatz p% (Berechne zunächst q und damit dann p%).
b) K0 = 5000€; p% = 4,5 = 0,045, also q = 1,045; Kn = 2 ∙ 5000€ = 10000€ ("verdoppelt")
ges: n
Löse durch Probieren!
c) geg: n = 8 Jahre; p% = 5,25% = 0,0525, also q = 1 + 0,0525 = 1,0525; K8 = 6776,25€
ges: K0
Vergleiche deine Lösungen zu den Aufgaben oben (bunte Mischung)
K0 = 500€; K0 = 4500€
p% = 1,2%; p% = 1%; p% = 3,5%; p% = 5,2%;
q=1,015; q = 1,01; q =1,03
Kn=8079,63€; Kn = 11685,39€; Kn = 11098,45€; Kn = 12208,29€
3.3 Anwendung des exponentiellen Wachstums: Halbwertszeit und Generationszeit (Verdopplungszeit)
Einstieg: evtl. Bierschaumzerfall (Untersuchtung auf leifiphysik)
Das nachfolgende Applet stellt den Zerfallsprozess anschaulich dar:
- Halbwertszeit (Atome)
Direkter Link: https://www.geogebra.org/m/cq62nsqj

Applet von Hegius, Mathezone
Das nachfolgende Applet stellt den Verdopplungsprozess anschaulich dar:
- Generationszeit/ Verdopplungszeit (Bakterien)
Direkter Link: passt das Applet??

Applet von Hegius, R. Schürz
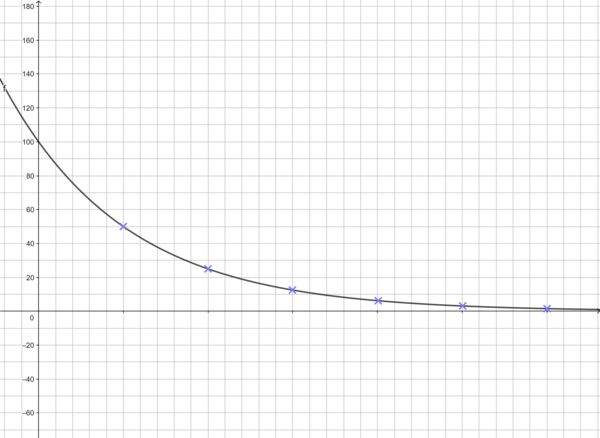
geg: Wismut 210 mit T = 5 Tage; q = 0,5 und Ausgangsmenge W0 = 100g.
Zeit = 30 Tage, in 5 Tagesabschnitten, also für n = 1, 2, 3, 4, 5 und 6
ges: Wertetabelle:
W1 = W0 · 0,51
= 100 · 0,5 = 50 (g)
W2 = W0 · 0,52
= 100 · 0,52 = 25 (g)
W3 = W0 · 0,53
= 100 · 0,53 = 12,5 (g)
...
geg: Radium-229 mit T = 240 s; q = 0,5 und Ausgangsmenge W0 = 48g.
Zeit = 6 Minuten = 360 s
ges: n; Wn
n = = = 1,5
geg: Radium-229 mit T = 240 s; q = 0,5 und Ausgangsmenge W0 = 48mg.
Wn = 1,5 mg
ges: n; t (Zeit)
1,5 = 48 · 0,5n
Löse durch systematisches Probieren.
geg: Generationszeit T2 = 45 Tage; W0 = 10 (Ratten); q = 2; t = 3 Monate = 90 Tage; n = = = 2
geg: Generationszeit T2 = 45 Tage = 1,5 Monate; q = 2; W0 = 10 (Ratten); Wn = 80 Mio;
ges: n; t
geg: n = 23 (wie in Nr. 8b)
geg: q = 2; W0 = 50 Bakterien; T2 = 30 Minuten = 0,5 Stunden; t= 3,5 Stunden; n = = = 7
geg: q = 2; T2 = 3 Wochen; Wn = 100·W0
ges: n; t
Wn = W0·qn | Setze q = 2 und Wn = 100·W0 ein
Löse durch systematisches Probieren.
ges: n; Wn
n = ≈ 6,4
Wn = W0 · qn
geg: W0 = 400; W18,8 = 2·400 = 800; n = 18,8
ges: q
Wn = W0 · qn
800 = 400 · q18,8 |:400
2 = q18,8 |
= q
1,038 ≈ q
geg: W0 = 400; n = 2h = 120min; q = 1,038
ges: Wn
geg: W0 = 100% (die gesamte Menge des Stoffe ist noch da); W6 = 100% - 34% = 66%; n = 6
ges: q
W6 = W0 · q6 | Umstellen nach q
= q
= q
0,933 ≈ q
Nun berechne die Halbwertszeit:
geg: W0 = 100%; Wn = 50%; q = 0,933
ges: n
Wn = W0 · qn
0,5 = 1 · 0,993n
Löse durch Probieren.
Für n = 9 gilt: W9 ≈ 0,54
Für n = 10 gilt: W10 ≈ 0,4998
geg: W0 = 100%; W24 = 300% (verdreifacht); n = 24
ges: q (prozentuales Wachstum pro Tag); p%
...
Einschub: Logarithmieren
Ist beim exponentiellen Wachstum der Exponent n gesucht, kannst du diesen Wert durch systematisches Probieren erhalten. Eine genauere Möglichkeit ist das Logarithmieren.
Falls du einen Taschenrechner nutzt, der diese Möglichkeit nicht hat, tippe wie folgt:
x =