Benutzer:Buss-Haskert/Terme/Terme mit Klammern: Unterschied zwischen den Versionen
K (Übungen ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (59 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== 3) Terme mit Klammern == | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Navigation| | |||
[[Benutzer:Buss-Haskert/Terme| Vorwissen zum Thema Terme]]<br> | |||
[[Benutzer:Buss-Haskert/Terme/Variablen und Terme|1) Variablen und Terme]]<br> | |||
[[Benutzer:Buss-Haskert/Terme/Terme vereinfachen|2) Terme vereinfachen]]<br> | |||
[[Benutzer:Buss-Haskert/Terme/Terme mit Klammern|3) Terme mit Klammern]]}} | |||
==3) Terme mit Klammern== | |||
Einstieg noch ergänzen! | Einstieg noch ergänzen! | ||
=== 3.1 Pluszeichen vor der Klammer === | ===3.1 Pluszeichen vor der Klammer=== | ||
{{Box|Pluszeichen vor der Klammer|Steht in einer Summe oder Differenz ein Pluszeichen vor der Klammer, kannst du die Klammer einfach weglassen. Die Rechenzeichen im Term ändern sich nicht.<br> | {{Box|Pluszeichen vor der Klammer|Steht in einer Summe oder Differenz ein Pluszeichen vor der Klammer, kannst du die Klammer einfach weglassen. Die Rechenzeichen im Term ändern sich nicht.<br> | ||
Merke dir als Bild den lachenden Smiley 🌝, denn diese Klammer aufzulösen ist sehr leicht!|Arbeitsmethode}} | Merke dir als Bild den lachenden Smiley 🌝, denn diese Klammer aufzulösen ist sehr leicht!|Arbeitsmethode}} | ||
| Zeile 20: | Zeile 27: | ||
</div> | </div> | ||
=== 3.2 Minuszeichen vor der Klammer === | {{Box|Übung 1|Löse auf der Seite realmath von den Übungen jeweils so viele Aufgaben, dass du die 300 Punkte-Marke knackst. Lade einen Screenshot im Modul Aufgaben hoch. | ||
* [https://realmath.de/Neues/Klasse8/terme/sutermloes01.php Übung a]|Üben}} | |||
===3.2 Minuszeichen vor der Klammer=== | |||
{{Box|Minuszeichen vor der Klammer|Steht in einer Summe oder Differenz ein Minuszeichen vor der Klammer, kannst du die Klammer auflösen, indem du die Rechenzeichen umdrehst:<br> | {{Box|Minuszeichen vor der Klammer|Steht in einer Summe oder Differenz ein Minuszeichen vor der Klammer, kannst du die Klammer auflösen, indem du die Rechenzeichen umdrehst:<br> | ||
aus + wird - <br> | aus + wird - <br> | ||
aus - wird + <br> | aus - wird + <br> | ||
Merke dir als Bild den Blitz [[Datei:Flash-1015467 1920.jpg|rahmenlos]], denn wenn du diese Klammer auflöst, musst du aufpassen!|Arbeitsmethode}} | Merke dir als Bild den Blitz [[Datei:Flash-1015467 1920.jpg|rahmenlos|40px]], denn wenn du diese Klammer auflöst, musst du aufpassen!|Arbeitsmethode}} | ||
Beispiele: <br> | Beispiele: <br> | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
5a <span style="color:red">'''-'''</span> (6b + 7a) |[[Datei:Flash-1015467 1920.jpg|rahmenlos]] Klammer auflösen (Zeichen umkehren)<br> | 5a <span style="color:red">'''-'''</span> (6b + 7a) |[[Datei:Flash-1015467 1920.jpg|rahmenlos|40px]]Klammer auflösen <small>(Zeichen umkehren)</small><br> | ||
= 5a - 6b - 7a |gleichartige Terme zusammenfassen<br> | = 5a - 6b - 7a |gleichartige Terme zusammenfassen<br> | ||
= -2a - 6b <br> | = -2a - 6b <br> | ||
</div> | </div> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
8x <span style="color:red">'''-'''</span> (-9y - 4x) |[[Datei:Flash-1015467 1920.jpg|rahmenlos]] Klammer auflösen (Zeichen umkehren)<br> | 8x <span style="color:red">'''-'''</span> (-9y - 4x) |[[Datei:Flash-1015467 1920.jpg|rahmenlos|40px]]Klammer auflösen <small>(Zeichen umkehren)</small><br> | ||
= 8x + 9y + 4x |gleichartige Terme zusammenfassen<br> | = 8x + 9y + 4x |gleichartige Terme zusammenfassen<br> | ||
= 12x + 9y | = 12x + 9y | ||
</div> | </div> | ||
</div> | </div> | ||
{{Box|Übung | <br> | ||
{{Box|Übung 2|Löse auf der Seite realmath von den Übungen jeweils so viele Aufgaben, dass du die 300 Punkte-Marke knackst. Lade einen Screenshot im Modul Aufgaben hoch. | |||
* [https://www.realmath.de/Neues/Klasse8/terme/sutermloes02.php Übung a] | |||
* [https://www.realmath.de/Neues/Klasse8/terme/sutermloes.php Übung b (Toplevel)]|Üben}} | |||
{{Box|Übung | {{Box|Übung 3|Bearbeite die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pgpizagbn20|width=100%|height=400px}} | |||
{{LearningApp|app=pxhvvnchk19|width=100%|height=400px}} | |||
{{LearningApp|app=pz9gbr89j19|width=100%|height=400px}} | |||
<br> | |||
{{Box|Übung 4|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-vereinfachen.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 20 | * 20 | ||
* 21|Üben}}<br> | * 21 | ||
{{Box|Übung | * 22 | ||
* 23 | |||
* 24|Üben}}<br> | |||
{{Box|Übung 5|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen übersichtlich und vollständig:<br> | |||
1. Schreibe zunächst die Aufgabe ab,<br> | 1. Schreibe zunächst die Aufgabe ab,<br> | ||
2. löse dann die Klammer auf und<br> | 2. löse dann die Klammer auf und<br> | ||
| Zeile 56: | Zeile 70: | ||
* S. 106 Nr. 2 | * S. 106 Nr. 2 | ||
* S. 106 Nr. 3|Üben}} | * S. 106 Nr. 3|Üben}} | ||
<br> | |||
{{Lösung versteckt|1=Vergleiche deine Lösungen und hake mit einem andersfarbigen Stift ab:<br> | |||
1a) m – n – o b) 23 + g – h c) 50 – k + m d) 32 + p – q e) –2x – 3y – 4z f) 3y + 2x – z<br> | |||
2 a) 6a + 8b b) 2a + 2b c) -6a + 2b d) 6a – 8b <br> | |||
3 a) 9m – 6n b) –9u – 2v c) –r – 10s d) 3,4d – 1,5c e) –4b + 6c + 6,1a|2=Vergleiche deine Lösungen|3=Verbergen}} | |||
===Teste dich - Plusklammer oder Minusklammer=== | |||
{{Box|Teste dich - Plusklammer 🌝 oder Minusklammer [[Datei:Flash-1015467 1920.jpg|rahmenlos|40px]]|Bearbeite das nachfolgende Quiz. | |||
* Wenn du weniger als 8 Punkte hast, übe mit den Links in den Übungen 1 und 2 (realmath). | |||
* Wenn du 8 oder mehr Punkte hast, kannst du im Lernpfad weitergehen.|Üben}} | |||
<br> | |||
{{h5p-zum|id=13429|height=400px}} | |||
=== 3.3 Malzeichen vor der Klammer (Ausmultiplizieren) === | ===3.3 Malzeichen vor der Klammer (Ausmultiplizieren)=== | ||
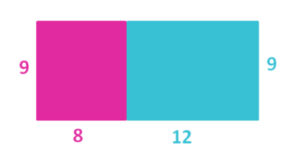
{{Box|Entdecken|[[Datei:Skizze Rechteck Distributivgesetz.png|links|300px]]Skizziere das Rechteck in dein Heft und berechne den Flächeninhalt des gesamten Rechtecks.<br> | |||
Findest du verschiedene Möglichkeiten? Notiere im Heft.|Arbeitsmethode}} | Findest du verschiedene Möglichkeiten? Notiere im Heft.|Arbeitsmethode}} | ||
| Zeile 69: | Zeile 92: | ||
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft. | Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft. | ||
{{Lösung versteckt|Das Gesetz heißt | {{Lösung versteckt|Das Gesetz heißt Verteilungsgesetz (Distributivgesetz). Wir haben dies umgangssprachlich auch "Jedem die Hand geben" genannt und die Hände als Tipp gezeichnet.[[Datei:Hand-1311786 1280.png|rahmenlos|40x40px]]|Lösung|Verbergen}} | ||
Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst. | Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.<br> | ||
Originallink https://www.geogebra.org/m/XcFmnc9X | |||
<ggb_applet id="XcFmnc9X" width="1072" height="600" border="888888" /> | <ggb_applet id="XcFmnc9X" width="1072" height="600" border="888888" /> | ||
<small>Applet von Birgit Lachner</small> | |||
<br> | |||
<br> | |||
Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen: | Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen: | ||
<br /> | <br /> | ||
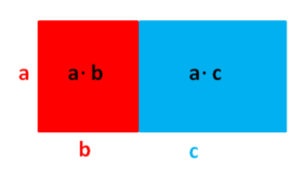
{{Box|Malzeichen vor der Klammer - Verteilungsgesetz (Distributivgesetz)| | {{Box|1=Malzeichen vor der Klammer - Verteilungsgesetz (Distributivgesetz)|2=Steht in einer Summe oder Differenz ein Malzeichen vor der Klammer, löst du die Klammer auf, indem du jeden Summanden in der Klammer mit dem Faktor multiplizierst.<br> | ||
<br /> | Merke dir als Bild die Hände [[Datei:Hand-1311786 1280.png|rahmenlos|40x40px]], denn wenn du diese Klammer auflöst, musst der Faktor jedem Summanden "die Hand geben".<br> | ||
[[Datei: | [[Datei:Rechteck Distributivgesetz allgemein.png|links|rahmenlos]]<br> | ||
a <span style="color:red">'''∙'''</span> (b + c) = a ∙ b + a ∙ c|3=Arbeitsmethode}} | |||
Beispiele: <br> | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
2a <span style="color:red">'''∙'''</span> (6b + 7a) |[[Datei:Hand-1311786 1280.png|rahmenlos|40x40px]]Klammer auflösen <small>("Jedem die Hand geben"</small>)<br> | |||
= 2a ∙ 6b + 2a ∙ 7a |Terme multiplizieren<br> | |||
= 12ab + 14a² <br> | |||
</div> | |||
<div class="width-1-2"> | |||
5x <span style="color:red">'''∙'''</span> (7y - 8x) |[[Datei:Hand-1311786 1280.png|rahmenlos|40x40px]]Klammer auflösen <small>("Jedem die Hand geben")</small><br> | |||
= 5x ∙ 7y - 5x ∙ 8x |Terme multiplizieren<br> | |||
= 35xy - 40x² | |||
</div> | |||
</div> | |||
<br> | |||
{{#ev:youtube|X5E2bqby8f0|800|center}} | |||
{{Box|Übung 6|Löse zur Übung die nachfolgenden LearningApps.|Üben}} | |||
{{LearningApp|app=pv9ujh6r520|width=100%|height=400px}} | |||
{{LearningApp|app=pq6j6ei0n21|width=100%|height=600px}} | |||
{{Box|Übung 7|Löse auf der Seite realmath von den Übungen jeweils so viele Aufgaben, dass du die 300 Punkte-Marke knackst. Lade einen Screenshot im Modul Aufgaben hoch. | |||
* [https://www.realmath.de/Neues/Klasse8/summenterme/distributiv.php Übung 1] | |||
* [https://www.realmath.de/Neues/Klasse8/summenterme/distributiv02.php Übung 2] | |||
* [https://www.realmath.de/Neues/Klasse8/summenterme/distributiv03.php Übung 3 (Profilevel)]|Üben}} | |||
{{Box|Übung 8|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-vereinfachen.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 25 | |||
* 26 | |||
* 27 | |||
* 28 | |||
* 29 | |||
* 30 | |||
* 31 | |||
* 32|Üben}}<br> | |||
{{Box|Übung 9|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen übersichtlich und vollständig:<br> | |||
1. Schreibe zunächst die Aufgabe ab,<br> | |||
2. löse dann die Klammer auf und<br> | |||
3. fasse zum Schluss so weit wie möglich zusammen. | |||
* S. 106 Nr. 5 | |||
* S. 106 Nr. 6 | |||
* S. 106 Nr. 7 | |||
* S. 106 Nr. 9|Üben}} | |||
{{Lösung versteckt|1=Das Verteilungsgesetz gilt auch für die Division, also wenn ein Geteilt-Zeichen hinter der Klammer steht. Teile jeden Summanden der Klammer durch den Divisor.<br> | |||
b) (18u + 9w) : 3<br>= 18u:3 + 9w:3<br>= 6u + 3w | |||
|2=Tipp zu Nr. 9|3=Verbergen}} | |||
{{Box|Übung 10|Finde den Fehler und schreibe die Aufgabe korrigiert in dein Heft. | |||
* S. 106 Nr. 8|Üben}} | |||
{{#ev:youtube|emkfgtY8B8s|800|center}} | |||
{{Box|Übung 11 - Ausklammern (Faktorisieren)|Löse die nachfolgenden LearningApps.|Üben}} | |||
{{LearningApp|app=p4ffs9drk25|width=100%|height=400px}} | |||
{{Box|Übung 12 - Ausklammern (Faktorisieren)|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen ausführlich und vollständig: | |||
* S. 106, Nr. 10 | |||
* S. 106, Nr. 11|Üben}} | |||
===Teste dich - Ausmultiplizieren=== | |||
{{Box|Teste dich - Malzeichen vor der Klammer [[Datei:Hand-1311786 1280.png|rahmenlos|40x40px]]|Bearbeite das nachfolgende Quiz. | |||
* Wenn du weniger als 4 Punkte hast, übe mit den Links von Übung 7. | |||
* Wenn du 4 oder mehr Punkte hast, bist du bereit für die Checkliste.|Üben}} | |||
<br> | |||
{{h5p-zum|id=13430|height=400px}} | |||
===Kompkexe Terme vereinfachen=== | |||
{{#ev:youtube|3otUNZum1Ig|800|center|||start=215&end=540}} | |||
{{Box|Übung 13 - Komplexe Terme (Profi)|Löse die Aufgabe aus dem Buch. Achte auf eine übersichtliche und vollständige Darstellung. | |||
* S. 110, Nr. 12|Üben}} | |||
{{ | {{Lösung versteckt|1= | ||
a) 6(5m + 4n) <span style="color:red">-4</span>(2n + m) <span style="color:red">-5</span>(5m + 3n) Malklammer, ausmultiplizieren mit 6, -4 und -5!<br> | |||
= 30m + 24n - 8n - 4m - 25m - 15n<br> | |||
= 30m - 4m - 25m + 24n - 8n - 15n<br> | |||
= 1m + 1n<br> | |||
b) 9a(5c - 3b) + (7b - 11c)·4a Malklammer, ausmultiplizieren; beim letzten Ausdruck steht der Faktor HINTER der Klammer<br> | |||
= 45ac - 27ab + 28ab - 44ac<br> | |||
= 45ac - 44ac - 27ab + 28ab<br> | |||
= 1ac + 1ab<br> | |||
c) 2(22s - 18t²) - (12t² - 15s)·(-3) 1. Ausmultiplizieren, 2. Minusklammer und Malklammer (HINTEN)<br> | |||
= 44s - 36t² - (-36t² + 45s)<br> | |||
= 44s - 36t² + 36t² - 45s<br> | |||
= 44s - 45s - 36t² + 36t² | |||
= -1s<br> | |||
d) (-12a + 20b)·15x - 20x(14b - 9a)<br> | |||
= -180ax + 300bx - 280bx + 180ax<br> | |||
= -180ax + 180ax + 300bx - 280bx<br> | |||
= 20bx<br> | |||
e) 12m(8n + 9m) - (16n + 18m - p)·6m<br> | |||
= 96mn + 108m² - 96 mn - 108m² + 6mp<br> | |||
=6mp | |||
|2=Lösungen zu Nr. 12|3=Verbergen}} | |||
Aktuelle Version vom 7. Dezember 2025, 18:26 Uhr
3) Terme mit Klammern
Einstieg noch ergänzen!
3.1 Pluszeichen vor der Klammer
Beispiele:
2a + (3b + 4a) |🌝 Klammer auflösen (weglassen)
= 2a + 3b + 4a |gleichartige Terme zusammenfassen
= 6a + 3b
-4x + (2y - 6x) |🌝 Klammer auflösen (weglassen)
= -4x + 2y - 6x |gleichartige Terme zusammenfassen
= -10x + 2y
3.2 Minuszeichen vor der Klammer
Beispiele:
Vergleiche deine Lösungen und hake mit einem andersfarbigen Stift ab:
1a) m – n – o b) 23 + g – h c) 50 – k + m d) 32 + p – q e) –2x – 3y – 4z f) 3y + 2x – z
2 a) 6a + 8b b) 2a + 2b c) -6a + 2b d) 6a – 8b
Teste dich - Plusklammer oder Minusklammer
3.3 Malzeichen vor der Klammer (Ausmultiplizieren)
Vergleiche deine Ideen mit denen im nachfolgenden Video:
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.
Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.
Originallink https://www.geogebra.org/m/XcFmnc9X

Applet von Birgit Lachner
Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:
Beispiele:
Das Verteilungsgesetz gilt auch für die Division, also wenn ein Geteilt-Zeichen hinter der Klammer steht. Teile jeden Summanden der Klammer durch den Divisor.
= 18u:3 + 9w:3
= 6u + 3w
Teste dich - Ausmultiplizieren
Kompkexe Terme vereinfachen
a) 6(5m + 4n) -4(2n + m) -5(5m + 3n) Malklammer, ausmultiplizieren mit 6, -4 und -5!
= 30m + 24n - 8n - 4m - 25m - 15n
= 30m - 4m - 25m + 24n - 8n - 15n
= 1m + 1n
b) 9a(5c - 3b) + (7b - 11c)·4a Malklammer, ausmultiplizieren; beim letzten Ausdruck steht der Faktor HINTER der Klammer
= 45ac - 27ab + 28ab - 44ac
= 45ac - 44ac - 27ab + 28ab
= 1ac + 1ab
c) 2(22s - 18t²) - (12t² - 15s)·(-3) 1. Ausmultiplizieren, 2. Minusklammer und Malklammer (HINTEN)
= 44s - 36t² - (-36t² + 45s)
= 44s - 36t² + 36t² - 45s
= 44s - 45s - 36t² + 36t²
= -1s
d) (-12a + 20b)·15x - 20x(14b - 9a)
= -180ax + 300bx - 280bx + 180ax
= -180ax + 180ax + 300bx - 280bx
= 20bx
e) 12m(8n + 9m) - (16n + 18m - p)·6m
= 96mn + 108m² - 96 mn - 108m² + 6mp