Benutzer:Ansgar WWU-6/Anwendungsaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{Box|1= <span style="color: | {{Box|1= <span style="color: blau">Aufgabe: Elternsprechtag</span>|2= | ||
[[Datei:Parking-825371 1920.jpg|rechts|rahmenlos|300x300px]] | [[Datei:Parking-825371 1920.jpg|rechts|rahmenlos|300x300px]] | ||
Jedes halbe Jahr veranstaltet | Jedes halbe Jahr veranstaltet eine Schule einen Elternsprechtag von 12 Uhr bis 18 Uhr. Den Eltern stehen auf dem Lehrerparkplatz aber nur eine begrenzte Anzahl an Parkplätzen zur Verfügung, sodass die Schulleitung rechtzeitig entscheiden muss, ob noch weitere Parkplätze angemietet werden müssen. Sie geht davon aus, dass der erste Parkplatz erst nach Beginn des Elternsprechtages belegt wird und spätestens um 18 Uhr das letzte Auto den Parkplatz verlassen hat. | ||
Diesen Elternsprechtag stehen den Eltern 50 Parkplätze zur Verfügung. Eine Zählung um 13 Uhr ergibt, dass bereits die Hälfte der zur Verfügung stehenden Parkplätze belegt ist. | |||
| Zeile 16: | Zeile 17: | ||
a) | a) | ||
<br /><br /> | <br /><br /> | ||
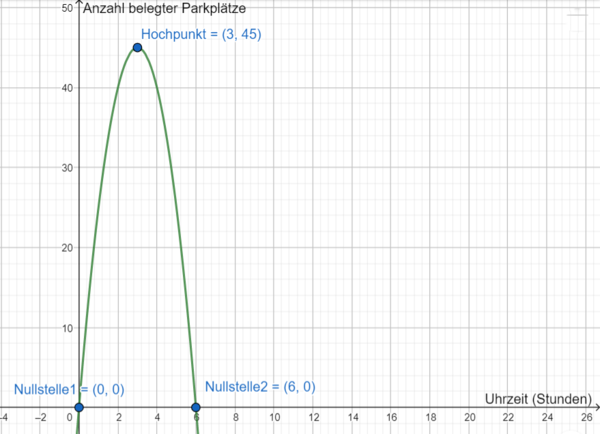
Die Anzahl belegter Parkplätze lässt sich in Abhängigkeit zur Uhrzeit (mit <math>t</math> in Stunden, wobei <math>t = 0</math> 12 Uhr repräsentiert) durch eine quadratische Funktion der Form <math>f(t) = at^2 + bt + c</math> beschreiben. Löse zunächst unteren Lückentext und stelle anschließend mit dessen Hilfe die Gleichung von <math>f</math> auf. | |||
Löse zunächst | |||
| Zeile 197: | Zeile 185: | ||
{{Lösung versteckt|1=[[Datei:Graph 1c.png|zentriert|rahmenlos|600x600px]]|2=Lösung|3=Lösung ausblenden}} | {{Lösung versteckt|1=[[Datei:Graph 1c.png|zentriert|rahmenlos|600x600px]]|2=Lösung|3=Lösung ausblenden}} | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
Aktuelle Version vom 14. April 2020, 15:41 Uhr
Anwendungsaufgaben