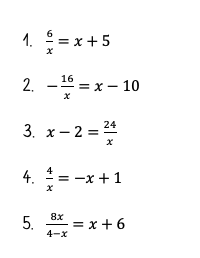Mathematik und Informatik MPR/Mathematik Klasse 9: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
(→Körper) Markierung: Quelltext-Bearbeitung 2017 |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
{{Box|Tipp|Schaut im Buch auf S. 36 und S. 37 die Beispielaufgaben an. | |||
Die quadratische Ergänzung funktioniert immer gleich. | |||
Die quadratische Ergänzung funktioniert immer gleich. Wir ergänzen immer auf beiden Seiten der Gleichung <math>\left ( \frac{b}{2} \right )^2</math>. | Wir ergänzen immer auf beiden Seiten der Gleichung <math>\left ( \frac{b}{2} \right )^2</math>. b ist dabei die Zahl, die vor dem x steht.|Unterrichtsidee }} | ||
| Zeile 116: | Zeile 114: | ||
<ggb_applet id="yqzyaEzf" width="600" height="400" /> | <ggb_applet id="yqzyaEzf" width="600" height="400" /> | ||
===Körper=== | |||
{{Box| Arbeitsauftrag| Bearbeitet die Aufgaben im Arbeitsplan. Nutzt hierzu die Padlet Seite [https://padlet.com/mprridinger/4p26gt98am0k unter diesem Link]. Solltet ihr Fragen haben, könnt ihr diese auf der Fragentafel notieren ([https://zumpad.zum.de/p/ojBBIIZVzx Link auf Seite]) Eine Übersicht zu allen Inhalten zu diesem Thema findet ihr [https://padlet.com/mprridinger/4p26gt98am0k auf dieser Seite.] |Arbeitsmethode}} | |||
Aktuelle Version vom 17. März 2020, 07:38 Uhr
Quadratische Gleichungen und Bruchgleichungen
Hier findest du Übungsaufgaben, sowie Erklärungen zu dem Thema Quadratische Gleichungen und Bruchgleichungen.
Rein Quadratische Gleichungen
Noch im Aufbau
Gemischt Quadratische Gleichungen
Satz vom Nullprodukt
Quadratische Ergänzung
ACHTUNG! Wenn ihr im Internet nach der quadratischen Ergänzung sucht, findet ihr oft die Ergänzung als Bestandteil von Parabeln. Das haben wir noch nicht gemacht. des Weiteren gibt es zwei Formen der quadratischen Ergänzung. Wir haben bisher nur eine gemacht. Deshalb seid vorsichtig, dass ihr euch nicht selbst verwirrt.
Beispiel:
Die Zahl, die vor dem x steht (die also mit einem "Mal Zeichen" mit x verbunden ist) ist die 2. Das heißt wir setzen für b die Zahl 2 ein.
Daraus folgt:
Nun entsteht eine Binomische Formel. In diesem Fall die erste. Falls du die binomischen Formeln nicht mehr kennst klicke folgenden Link.
Wir dürfen schreiben:
Lösungsformel
Noch im Aufbau
Bruchgleichungen
Beispiel
1. x1 = 1; x2 = -6 2. x1 = 8; x2 = 2 3. x1 = 6; x2 = -4 4. Keine Lösung 5. x1 = 2; x2 = -12
Ähnlichkeit
Vergrößern und Verkleinern