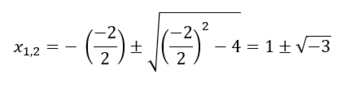Benutzer:Elena Jedtke/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Quelltext aus [[Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Terme und Gleichungen|Terme und Gleichungen]]: | |||
{{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> | |||
<span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> | |||
<span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> | |||
{{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} | |||
{{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel | |||
<math> x_{1,2} = - \frac{-2}{2} \pm \sqrt{\left( \frac{-2}{2} \right) ^2 -4}= 1 \pm \sqrt{-3}</math> | |||
, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. <br /> '''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} | |||
|3=Arbeitsmethode }} | |||
Nicht verstandene Mathe-Formel durch Foto ersetzt: | |||
{{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> | |||
<span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> | |||
<span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> | |||
{{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} | |||
{{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. | |||
[[Datei:TG Lösung zu A7.3a.png|350px|Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)]] | |||
'''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} | |||
|3=Arbeitsmethode }} | |||
===Spielwiese=== | ===Spielwiese=== | ||
| Zeile 110: | Zeile 141: | ||
|2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | |2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
Aktuelle Version vom 29. November 2019, 14:55 Uhr
Quelltext aus Terme und Gleichungen:
Nicht verstandene Mathe-Formel durch Foto ersetzt:
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz einfach per Mausklick aktivierbar
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
LearningApp:
Geogebra-Applet:

Kombinationen
Quadratische Funktionen in Scheitelpunktform
(Inhalte aus dem Lernpfad Quadratische Funktionen erkunden)