Geometrie im Dreieck/Triangle-Architects: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 4: | Zeile 4: | ||
| 2 = In diesem Lernpfadkapitel lernst du 3 Kongruenzsätze kennen, wie du Konstruktionsbeschreibungen erstellst und umsetzt. | | 2 = In diesem Lernpfadkapitel lernst du 3 Kongruenzsätze kennen, wie du Konstruktionsbeschreibungen erstellst und umsetzt. | ||
Für die Bearbeitung dieses Kapitels benötigst du das Arbeitsblatt "Triangle Architects", einen Zirkel, ein Geodreieck und einen Bleistift. | Für die Bearbeitung dieses Kapitels benötigst du das [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Arbeitsblatt "Triangle Architects", einen Zirkel, ein Geodreieck und einen Bleistift. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 66: | Zeile 66: | ||
{{Box|Aufgabe 2.3: Fertigstellen einer Konstruktion mit SWS|{{Lösung versteckt | | {{Box|Aufgabe 2.3: Fertigstellen einer Konstruktion mit SWS|{{Lösung versteckt | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS. Gegeben sind b <math> = </math> 5cm, c <math> = </math> 9cm und α <math> = </math> 55°. Wir haben mit der Konstruktion schon angefangen. Stelle die Konstruktion auf dem '''Arbeitsblatt '''"Triangle Architects" fertig. | ||
Konstruiere das Dreieck mit SWS. Gegeben sind b <math> = </math> 5cm, c <math> = </math> 9cm und α <math> = </math> 55°. Wir haben mit der Konstruktion schon angefangen. Stelle die Konstruktion auf dem '''Arbeitsblatt '''"Triangle Architects" fertig. | |||
[[Datei:SWS 2 Planfigur.png|thumb|Planfigur für Aufgabe 2.3|400 px| center]] | [[Datei:SWS 2 Planfigur.png|thumb|Planfigur für Aufgabe 2.3|400 px| center]] | ||
{{Lösung versteckt|1=[[Datei:SWS 2 Lösung.png|thumb|Lösung für Aufgabe 2.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | {{Lösung versteckt|1=[[Datei:SWS 2 Lösung.png|thumb|Lösung für Aufgabe 2.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
| Zeile 75: | Zeile 74: | ||
{{Box|Aufgabe 2.4: Durchführung einer Konstruktion mit SWS|{{Lösung versteckt | | {{Box|Aufgabe 2.4: Durchführung einer Konstruktion mit SWS|{{Lösung versteckt | | ||
Konstruiere das Dreieck mit SWS auf dem '''Arbeitsblatt'''. Gegeben sind b <math> = </math> 8cm, c <math> = </math> 3cm und α <math> = </math> 80°. Führe dazu alle Schritte A-D durch. | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit SWS auf dem '''Arbeitsblatt'''. Gegeben sind b <math> = </math> 8cm, c <math> = </math> 3cm und α <math> = </math> 80°. Führe dazu alle Schritte A-D durch. | ||
{{Lösung versteckt|1=[[Datei:SWS 3 Lösung.png|thumb|Lösung für Aufgabe 2.4|400 px| center]] |2= Lösung|3= Lösung verbergen}} | {{Lösung versteckt|1=[[Datei:SWS 3 Lösung.png|thumb|Lösung für Aufgabe 2.4|400 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | | Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | ||
| Zeile 128: | Zeile 127: | ||
{{Box|Aufgabe 3.3: Durchführung einer Konstruktion mit WSW|{{Lösung versteckt | | {{Box|Aufgabe 3.3: Durchführung einer Konstruktion mit WSW|{{Lösung versteckt | | ||
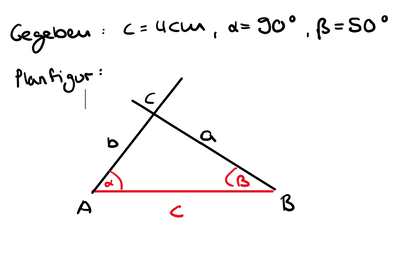
Konstruiere das Dreieck mit WSW auf dem '''Arbeitsblatt'''. Gegeben sind c <math> = </math> 4cm, α <math> = </math> 90° und 𝝱 <math> = </math> 50°. Führe dazu alle Schritte A-D durch. Wir haben mit der Konstruktion schon angefangen. Stelle die Konstruktion fertig. | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Konstruiere das Dreieck mit WSW auf dem '''Arbeitsblatt'''. Gegeben sind c <math> = </math> 4cm, α <math> = </math> 90° und 𝝱 <math> = </math> 50°. Führe dazu alle Schritte A-D durch. Wir haben mit der Konstruktion schon angefangen. Stelle die Konstruktion fertig. | ||
[[Datei:WSW 3.3 Planfigur.png|thumb|Planfigur für Aufgabe 3.3|400 px| center]] | [[Datei:WSW 3.3 Planfigur.png|thumb|Planfigur für Aufgabe 3.3|400 px| center]] | ||
{{Lösung versteckt|1=[[Datei:WSW 3.3 Lösung.png|thumb|Lösung für Aufgabe 3.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | {{Lösung versteckt|1=[[Datei:WSW 3.3 Lösung.png|thumb|Lösung für Aufgabe 3.3|400 px| center]] |2= Lösung|3= Lösung verbergen}} | ||
Version vom 15. November 2024, 13:12 Uhr
Info
1. Einstieg
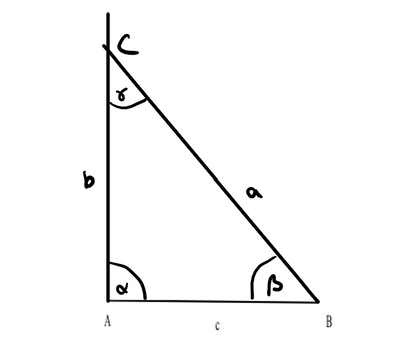
Zwischen Münster und Havixbeck steht die Burg Hülshoff. Vor etwa 200 Jahren wurde dort Annette Droste-Hülshoff geboren. Sie schrieb unter anderem das Gedicht "der Knabe im Moor". Zur Erinnerung an sie soll in den Burghof eine Bühne gebaut werden. Damit wurde das Architektenduo Achim-Alberta beauftragt. Das Duo hat bereits eine Idee und eine Skizze angefertigt (Siehe Bilder). Heute wollen sie zum Schloss fahren und messen wie groß die Bühne wird. Sie überlegen, welche Längen und Winkel sie messen müssen um die Bühne genau zu konstruieren.
Kannst du ihnen helfen? Welche Größen müssen Sie messen, um die Bühne zu kostruieren? Beschäftige dich dabei zunächst nur mit der Dreieckigen Grundfläche (Siehe Abbildung 3). Notiere dir die Größen, die sie deiner Meinung nach messen müssen auf einem Schmierpapier. Gibt es verschiedene Kombinationen die eine Konstruktion möglich machen? Überprüfe dich später selber.
2. Ein Dreieck konstruieren mit Seite Winkel Seite (SWS)
In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du die Länge von zwei Seiten und den dazwischen liegenden Winkel kennst. In der Box steht eine Anleitung, die dir das Konstruieren von Dreiecken erleichtert. Nutze die Anleitung für die folgenden Aufgaben.
Konstruieren bedeutet, dass du eine geometrische Figur schritt für schritt erstellst. Dabei musst du sehr genau arbeiten.
Planfigur: Eine Planfigur ist eine kleine Zeichnung, in der noch nicht alle Längen, Winkel und Größen richtig eingetragen sind. Du makierst dir die gegebene Größen, Winkel, Seiten bunt und hast hierdurch einen besseren Überblick.
Konstruktionsbeschreibung: Du schreibst in kleinen Schritten auf wie du ein Dreieck gezeichnet hast.
3. Ein Dreieck konstruieren mit Winkel Seite Winkel (WSW)
In diesem Kapitel lernst du, wie du ein Dreieck konstruieren kannst, wenn du zwei Winkel gegeben hast sowie die Seite, die zwischen diesen beiden Winkeln liegt.
4. Training macht den Meister
5. Triangle-Experts: Kann man mit drei Seiten immer ein Dreieck konstruieren?
In diesem Kapitel lernst du, wann man ein Dreieck konstruieren kann, wenn alle drei Seiten bekannt sind.
Super, du bist fertig! Gehe zurück zur Startseite Geometrie im Dreieck und bearbeite ein weiteres Kapitel!