Jakob Uni MS-14/Entwurf: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (28 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 35: | Zeile 35: | ||
==Merksatz== | ==Merksatz== | ||
{{Box|Aufgabe 1: Merksatz |Vervollständige den Merksatz und kontrolliere deine Lösung. Trage den Merksatz auf dem Arbeitsblatt ein. |Arbeitsmethode | {{Box|Aufgabe 1: Merksatz |Vervollständige den Merksatz und kontrolliere deine Lösung. Trage den Merksatz auf dem Arbeitsblatt ein. | ||
{{LearningApp|width=90%|height=300px|app=37688425}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
==Konstruktion== | ==Konstruktion== | ||
{{Box|Aufgabe 2.1: Konstruktionsaufgabe |Konstruiere mittels der in Geogebra gegebenen Werkzeuge den Umkreis des gegebenen Dreiecks. | |||
<ggb_applet id="bmjyge6v" width="550" height="450" /> | |||
|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe 2.2: Konstruktionsaufgabe |Konstruiere den Inkreis des gegebenen Dreiecks. | |||
<ggb_applet id="knbhdr7r" width="550" height="450" /> | |||
|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe 2.3: Konstruktionsaufgabe |Konstruiere den Schwerpunkt des gegebenen Dreiecks. | |||
<ggb_applet id="zbue4tyz" width="550" height="450" /> | |||
|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|Aufgabe 3.1 - 3.3: Konstruieren mit Zirkel und Lineal |Auf deinem Arbeitsblatt findest du Konstruktionsaufgaben, die du analog bearbeiten kannst. Hier findest du Tipps, falls du welche brauchst. | |||
|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | |||
==Eigenschaften== | |||
{{Box|Aufgabe 4.1: Charakteristische Punkte |Beantworte die Fragen. Du kannst dir mit den Tipps Hilfe holen. | |||
<quiz display="simple"> | |||
{Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein} | |||
+ Die Winkel α und β sind Nebenwinkel. | |||
- Die Winkel α und β sind Scheitelwinkel. | |||
+ Die Winkel ε und δ sind Stufenwinkel. | |||
- Die Winkel ζ und δ sind Wechselwinkel. | |||
{Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein} | |||
+ Scheitelwinkel sind immer gleich groß. | |||
- Wechselwinkel sind zusammen immer 90 Grad groß. | |||
- Die Winkel α und γ sind zusammen 180 Grad groß. | |||
+ Nebenwinkel sind immer zusammen 180 Grad groß. | |||
== | {Welche Aussage ist falsch?} | ||
+ Wenn α = 120° ist, dann ist θ = 120° | |||
| Farbe = {{Farbe|orange}} | + Wenn θ = 120° ist, dann ist ε = 60° | ||
- Wenn α = 60° ist, dann ist γ = 120° | |||
- Wenn ζ = 160° ist, dann ist γ = 20°. | |||
</quiz> | |||
|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
{{Box|Aufgabe | {{Box|Aufgabe 2.2: Ordne zu |Benenne die Punkte M<sub>1</sub>,M<sub>2</sub> und M<sub>3</sub> der dynamischen Grafik. Du kannst die Eckpunkte des Dreiecks bewegen. | ||
| Farbe = {{Farbe|orange}} | <ggb_applet id="srjcpuge" width="400" height="450" />|Arbeitsmethode| Farbe = {{Farbe|orange}} | ||
}} | }} | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Deine Lösung: | Deine Lösung: M<sub>1</sub> - '''Umkreismittelpunkt''', M<sub>2</sub> - '''Schwerpunkt''', M<sub>3</sub> - '''Inkreismittelpunkt''' | ||
M<sub>1</sub> - '''Umkreismittelpunkt''', M<sub>2</sub> - '''Schwerpunkt''', M<sub>3</sub> - '''Inkreismittelpunkt''' | |||
</div> | </div> | ||
==Schnappe die Diebe== | ==Schnappe die Diebe== | ||
{{Box|Aufgabe | {{Box|Aufgabe 5: Entfernungsproblem |Finde den Ort an dem Kommissar Biehl warten soll, damit er gleich schnell bei jedem möglichen Einbruchsort ist. Du kannst im Fenster mit Geogebra Konstruktionen durchführen. | ||
| Farbe = {{Farbe| | <ggb_applet id="rpsnggh3" width="720" height="520" /> | ||
{{Lösung versteckt|Kommissar Biehl sollte von jedem Einbruchsort gleichweit entfernt sein.|2=Tipp 1|3=Hilfe verbergen}} | |||
{{Lösung versteckt|Der Umkreismittelpunkt ist von jedem Eckpunkt eines Dreiecks gleich weit entfernt.|2=Tipp 2|3=Hilfe verbergen}}|Arbeitsmethode| Farbe = {{Farbe|orange}} | |||
}} | }} | ||
<ggb_applet id=" | |||
== Wiederholung == | |||
{{Box|1=Wiederholung: Umkreis- und Inkreismittelpunkt und Schwerpunkt eines Dreiecks|2=In Kapitel 3 (Aufgabe 4) habt ihr den Standort eines Hochseilgartens ermittelt, der von den drei Städten Münster, Paderborn und Bielefeld den gleichen Abstand haben soll. Dafür habt ihr den Schnittpunkt der Mittelsenkrechten ermittelt. Der Schnittpunkt der Mittelsenkrechten, hat von allen drei Eckpunkten des Dreiecks den gleichen Abstand und wird auch als '''Umkreismittelpunkt''' bezeichnet. | |||
<ggb_applet id="x7krntjr" width="100%" height="100%" /> | |||
Zusätzlich habt ihr in Kapitel 3 die Winkelhalbierenden wiederholt. Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt, der als '''Inkreismittelpunkt''' des Dreiecks bezeichnet wird. Der Inkreismittelpunkt hat von allen drei Seiten des Dreiecks den gleichen Abstand. | |||
(Geogebra Applet) | |||
Als weiteren wichtigen Punkt in einem Dreieck habt ihr den '''Schwerpunkt''' kennengelernt. Der Schwerpunkt ist der Schnittpunkt der Seitenhalbierenden. Auf einer Seitenhalbierenden liegt der Schwerpunkt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite. | |||
(GeoGebra Applet) }} | |||
==Aufgabe 1== | |||
{{Box | Aufgabe 1: | In einem Naturschutzgebiet kreuzen sich die drei Wanderwege a, b und c und bilden ein Dreieck. Es soll ein neuer Brunnen gebaut werden, der für Wanderer von allen drei Wegen gleich gut erreichbar ist. An welchem Punkt im Dreieck sollte der Brunnen gebaut werden, damit der Abstand zu jedem Wanderweg gleich ist? | Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
==Aufgabe 2== | |||
{{Box | Aufgabe 2:| Notiere zu jedem besonderen Punkt des Dreiecks die Kerneigenschaften.| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Lösung versteckt| | |||
Der Inkreismittelpunkt hat zu allen Seiten den gleichen Abstand. | |||
Der Umkreismittelpunkt hat zu allen Eckpunkten den gleichen Abstand. | |||
Der Schwerpunkt liegt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite. | |||
|Tipp anzeigen|Tipp verbergen}} | |||
Aktuelle Version vom 12. November 2024, 18:06 Uhr
Du hast dich nach Bearbeitung der Diagnoseaufgaben entschlossen dein Wissen über charakteristische Punkte des Dreiecks aufzufrischen. Solltest du auch bei den Voraussetzungen dieses Kapitels (den Seitenhalbierenden, Mittelsenkrechten und Winkelhalbierenden) noch Schwierigkkeiten haben, schau nochmal in das vorherige Kapitel in diesem Lernpfad. In deinem Mathebuch findest du das Thema auf den Seiten 56, 57 und 64.
Kapitel-Informationskästchen
Einstieg
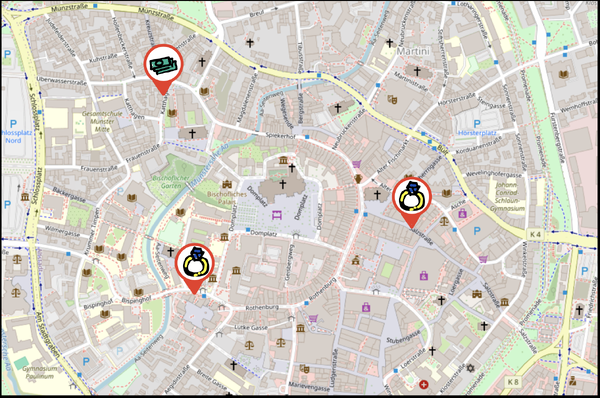
Ganz Münster ist in Angst versetzt. Einbrecher sind in der Stadt unterwegs. Doch Kommissar Biehl hat eine heiße Spur: er weiß wo der nächste Einbruch stattfinden wird. Leider kommen dafür zwei Juweliere und eine Bank infrage.
Kommissar Biehl muss natürlich schnellstmöglich vor Ort sein, um die Einbrecher auf frischer Tat zu ertappen. Wo soll er sich heute Nacht in der Stadt aufhalten, damit er schnell an jedem möglichen Einbruchsort sein kann?
Merksatz
Konstruktion
Eigenschaften
Deine Lösung: M1 - Umkreismittelpunkt, M2 - Schwerpunkt, M3 - Inkreismittelpunkt
Schnappe die Diebe
Wiederholung
Aufgabe 1
Aufgabe 2
Der Inkreismittelpunkt hat zu allen Seiten den gleichen Abstand.
Der Umkreismittelpunkt hat zu allen Eckpunkten den gleichen Abstand.
Der Schwerpunkt liegt immer auf 2/3 der Strecke vom Eckpunkt bis zur gegenüberliegenden Seite.