Jakob Uni MS-14/Entwurf: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 59: | Zeile 59: | ||
==Schnappe die Diebe== | ==Schnappe die Diebe== | ||
{{Box|Aufgabe 4: Entfernungsproblem |Finde den Ort an dem Kommissar Biehl warten soll, damit er zu gleich schnell bei jedem Einbruchsort wäre. |Arbeitsmethode | |||
| Farbe = {{Farbe|lila}} | |||
}} | |||
<ggb_applet id="rpsnggh3" width="720" height="520" /> | <ggb_applet id="rpsnggh3" width="720" height="520" /> | ||
Version vom 11. November 2024, 19:57 Uhr
Du hast dich nach Bearbeitung der Diagnoseaufgaben entschlossen dein Wissen über charakteristische Punkte des Dreiecks aufzufrischen. Solltest du auch bei den Voraussetzungen dieses Kapitels (den Seitenhalbierenden, Mittelsenkrechten und Winkelhalbierenden) noch Schwierigkkeiten haben, schau nochmal in das vorherige Kapitel in diesem Lernpfad. In deinem Mathebuch findest du das Thema auf den Seiten 56, 57 und 64.
Kapitel-Informationskästchen
Einstieg
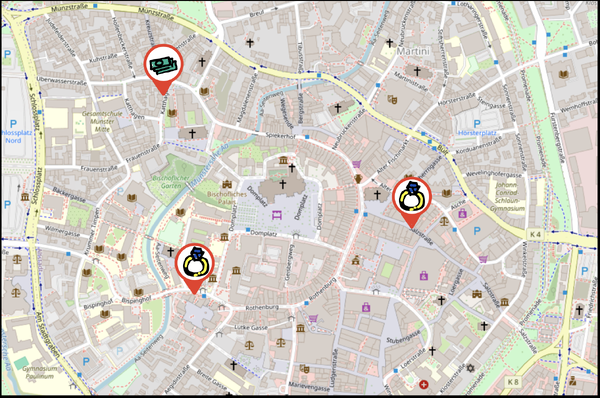
Ganz Münster ist in Angst versetzt. Einbrecher sind in der Stadt unterwegs. Doch Kommissar Biehl hat eine heiße Spur: er weiß wo der nächste Einbruch stattfinden wird. Leider kommen dafür zwei Juweliere und eine Bank infrage.
Kommissar Biehl muss natürlich schnellstmöglich vor Ort sein, um die Einbrecher auf frischer Tat zu ertappen. Wo soll er sich heute Nacht in der Stadt aufhalten, damit er schnell an jedem möglichen Einbruchsort sein kann?
Merksatz
Konstruktion
Eigenschaften

Deine Lösung:
M1 - Umkreismittelpunkt, M2 - Schwerpunkt, M3 - Inkreismittelpunkt
Schnappe die Diebe