Geometrie im Dreieck/Mehr als eine Linie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (91 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Zum Nachlesen== | |||
Falls du dich bei diesem Thema nicht mehr sicher fühlst und lieber zu Beginn oder zwischendurch dein Vorwissen auffrischen möchtest, kannst du dafür in deinem Mathebuch die Zusammenfassung des Kapitels 2 auf S. 70 verwenden und darüber hinaus folgende Seiten: | |||
Mittelsenkrechte - S. 56 | |||
Winkelhalbierende - S. 57 | |||
Seitenhalbierende - S. 64 | |||
==Einstieg== | |||
[[Datei:Marias Zeichnung.png|mini|Marias Zeichnung]] | [[Datei:Marias Zeichnung.png|mini|Marias Zeichnung]] | ||
{{Box|Denk nach!|Martin und Maria sollen als Hausaufgabe in ein gleichseitiges Dreieck die Mittelsenkrechten, die Winkelhalbierenden und die Seitenhalbierenden einzeichnen. Maria behauptet, sie hätte alle Linien eingezeichnet. Martin meint, sie hätte die Mittelsenkrechten und die Seitenhalbierenden vergessen. Was meinst du? Begründe deine Antwort. |Arbeitsmethode| Farbe={{Farbe|grau}} }} | {{Box|Denk nach!|Martin und Maria sollen als Hausaufgabe in ein gleichseitiges Dreieck die Mittelsenkrechten, die Winkelhalbierenden und die Seitenhalbierenden einzeichnen. Maria behauptet, sie hätte alle Linien eingezeichnet. Martin meint, sie hätte die Mittelsenkrechten und die Seitenhalbierenden vergessen. Was meinst du? Begründe deine Antwort. Schreibe auf das Arbeitsblatt. |Arbeitsmethode| Farbe={{Farbe|grau}} }} | ||
==Aufgabe 1: Eigenschaften zuordnen== | |||
{{Box|Aufgabe 1| Ordne die Aussagen den Linien zu. {{LearningApp|app=pj8oiu93a24|width=100%|height=400px}}|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |||
==Aufgabe 2: Besondere Linien konstruieren 1== | |||
{{Box|Grundlegende Kompetenzen|{{Lösung versteckt | | |||
Fülle die Lücken des folgenden Textes, indem du das richtige Wort aus den Vorschlägen auswählst. | |||
{{LearningApp|app=pt908oc6224|width=100%|height=400px}} | |||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode| Farbe={{Farbe|orange}} }} | |||
{{Box|mittlere Schwierigkeit|{{Lösung versteckt | | |||
Fülle die Lücken des folgenden Textes. | |||
{{LearningApp|app=p77ndiean24|width=100%|height=400px}} | |||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode | Farbe = #CD2990 }} | |||
{{Box|erhöhte Schwierigkeit|{{Lösung versteckt | | |||
Beschreibe in eigenen Worten auf dem Arbeitsblatt, wie du die folgenden Linien mit dem Zirkel konstruieren kannst: | |||
a) Winkelhalbierende | |||
{{Lösung versteckt | Die folgenden Punkte sollten in deiner Lösung enthalten sein: | |||
- um den Eckpunkt einen Kreis zeichnen | |||
- um die Schnittpunkte des Kreises mit den Schenkeln erneut Kreise zeichnen | |||
- die Schnittpunkte der beiden neuen Kreise mit dem Eckpunkt durch eine Gerade verbinden | |||
| Lösung anzeigen | Lösung verbergen}} | |||
b) Mittelsenkrechte | |||
{{Lösung versteckt | Die folgenden Punkte sollten in deiner Lösung enthalten sein: | |||
- um beide Eckpunkte einen Kreis einzeichnen | |||
- Kreise müssen den gleichen Radius haben und der Radius muss größer als die halbe Seitenlänge sein | |||
- die Schnittpunkte der beiden Kreise durch eine Gerade verbinden | |||
| Lösung anzeigen | Lösung verbergen}} | |||
c) Seitenhalbierende | |||
{{Lösung versteckt | Die folgenden Punkte sollten in deiner Lösung enthalten sein: | |||
- um beide Eckpunkte einen Kreis einzeichnen | |||
- Kreise müssen den gleichen Radius haben und der Radius muss größer als die halbe Seitenlänge sein | |||
- die Schnittpunkte der beiden Kreise durch eine Gerade verbinden; der Schnittpunkt dieser Gerade mit der Seite ist der Mittelpunkt der Seite | |||
- den Mittelpunkt der Seite mit der gegenüberliegenden Ecke durch eine Strecke verbinden | |||
| Lösung anzeigen | Lösung verbergen}} | |||
| Aufgabe anzeigen | Aufgabe verbergen}}|Arbeitsmethode }} | |||
==Aufgabe 3: Besondere Linien konstruieren 2== | |||
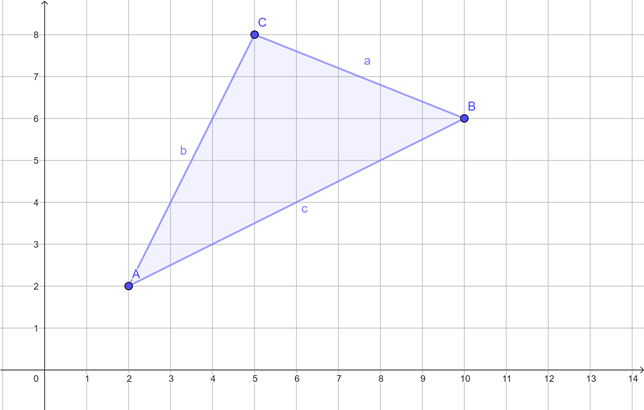
{{Box|Aufgabe 3|Konstruiere folgende Linien mit Geodreieck oder Zirkel. Nutze dafür das Arbeitsblatt. | |||
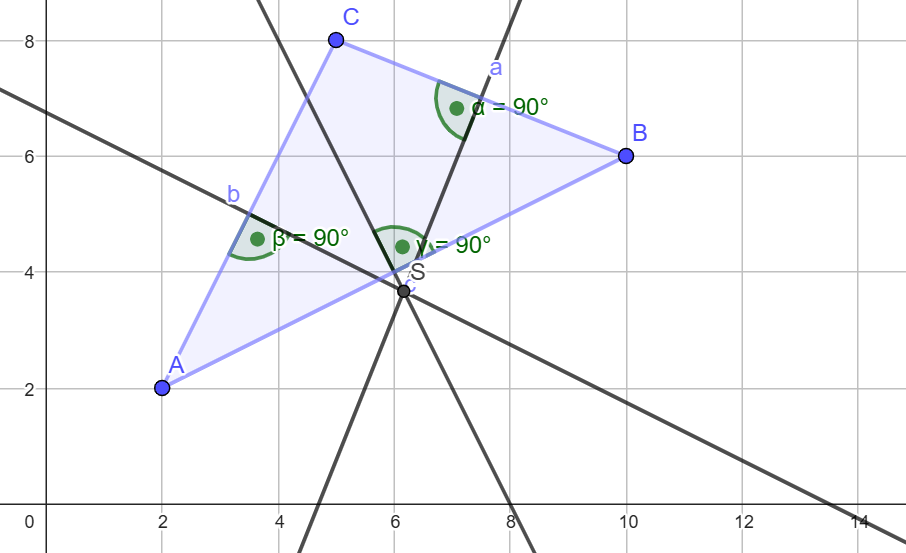
a) Mittelsenkrechte | |||
[[Datei:Image 2.png]] | |||
{{Lösung versteckt|[[Datei:Image 3.png]] | Lösung anzeigen | Lösung verbergen}} | |||
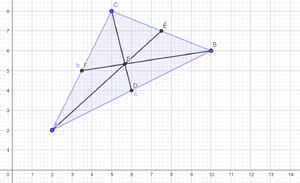
b) Seitenhalbierende | |||
[[Datei:Image 2.png]] | |||
{{Lösung versteckt|[[Datei:Image 4.png|mini]]| Lösung anzeigen | Lösung verbergen}} | |||
c) Winkelhalbierende | |||
[[Datei:Image 2.png]] | |||
{{Lösung versteckt|[[Datei:Image 5.png]]| Lösung anzeigen | Lösung verbergen}} | |||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |||
==Aufgabe 4: Anwendungsaufgabe== | |||
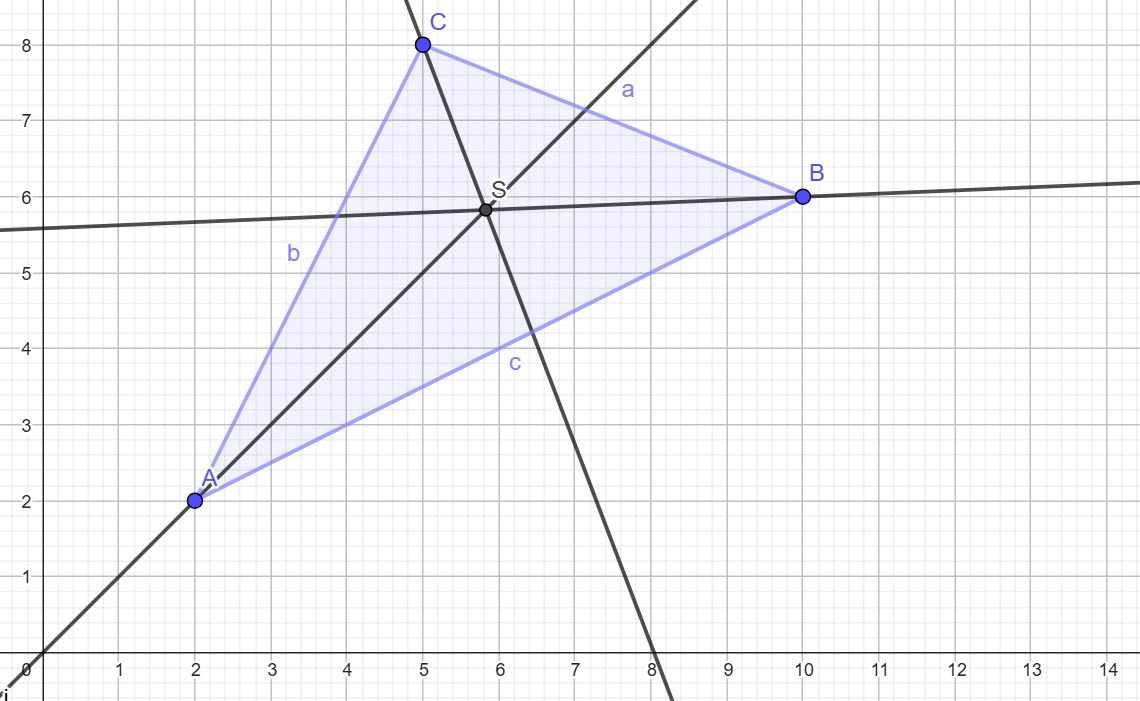
{{Box|Aufgabe 4|Die drei Städte Münster, Bielefeld und Paderborn möchten zusammen einen Hochseilgarten bauen. Der Eingang vom Hochseilgarten soll von allen drei Städten gleich weit entfernt sein. | |||
a) Bestimme die Koordinaten des Eingangs. Nutze zur Bestimmung der Koordinaten des Eingangs [https://www.geogebra.org/calculator/wecpxpj6 dieses GeoGebra-Applet]. | |||
{{Lösung versteckt|Überlege, welche der drei besonderen Linien im Dreieck den gleichen Abstand zu den Eckpunkten hat. | 1. Tipp anzeigen | 1. Tipp verbergen}} | |||
{{Lösung versteckt|Nutze die Mittelsenkrechten.| 2. Tipp anzeigen | 2. Tipp verbergen}} | |||
{{Lösung versteckt|Das GeoGebra-Applet mit der Lösung findest du [https://www.geogebra.org/calculator/x7krntjr hier]. Also muss der Eingang vom Hochseilgarten im Punkt S(6,57; 5,71) liegen.| Lösung anzeigen | Lösung verbergen}} | |||
b) Beurteile, ob dieses Modell realitätsnah ist und welche Vereinfachungen du angenommen hast. | |||
{{Lösung versteckt|Zu beachten sind zum Beispiel folgende Vereinfachungen: | |||
- Der Eingang befindet sich eigentlich nie nur an einem Punkt. | |||
- Eventuell befindet sich an diesem Ort gar keine freie Fläche. | |||
- Die Luftlinie entspricht nicht der tatsächlichen Straßenführung. Es kann also trotzdem unterschiedlich lange Anreisezeiten geben. | |||
- ... | |||
| Lösung anzeigen | Lösung verbergen}} | |||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |||
Version vom 11. November 2024, 14:24 Uhr
Zum Nachlesen
Falls du dich bei diesem Thema nicht mehr sicher fühlst und lieber zu Beginn oder zwischendurch dein Vorwissen auffrischen möchtest, kannst du dafür in deinem Mathebuch die Zusammenfassung des Kapitels 2 auf S. 70 verwenden und darüber hinaus folgende Seiten:
Mittelsenkrechte - S. 56
Winkelhalbierende - S. 57
Seitenhalbierende - S. 64
Einstieg
Aufgabe 1: Eigenschaften zuordnen
Aufgabe 2: Besondere Linien konstruieren 1