Benutzer:Buss-Haskert/Terme/Variablen und Terme: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 45: | Zeile 45: | ||
Entscheide, ob es sich um eine Variable, einen Term oder keins von beidem handelt:<br> | Entscheide, ob es sich um eine Variable, einen Term oder keins von beidem handelt:<br> | ||
{{LearningApp|app=pwfg84p2c20|width=100%|height=600px}}<br> | {{LearningApp|app=pwfg84p2c20|width=100%|height=600px}}<br> | ||
Originallink: https://www.geogebra.org/m/svqmvxnp<br> | |||
<ggb_applet id="bzmav24s" width="800" height="425" border="888888" /> | |||
<small>Applet des FLINK-Teams</small> | |||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 75: | Zeile 78: | ||
===1.2 Werte von Termen berechnen=== | ===1.2 Werte von Termen berechnen=== | ||
{{Box|Die Term Maschine|Beschreibe, wie die Term Maschine funktioniert|Unterrichtsidee}} | {{Box|Die Term Maschine|Beschreibe, wie die Term Maschine funktioniert|Unterrichtsidee}} | ||
Originallink: https://www.geogebra.org/m/n6cttesM <br> | |||
{{h5p-zum|id=13444|height=600px}} | {{h5p-zum|id=13444|height=600px}} | ||
<small>von Beraterinnen und Beratern für Unterrichtsentwicklung Mathematik</small> | <small>von Beraterinnen und Beratern für Unterrichtsentwicklung Mathematik</small> | ||
<br><br> | <br><br> | ||
| Zeile 98: | Zeile 100: | ||
{{LearningApp|app=pzx50fvs523|width=100%|height=500px}} | {{LearningApp|app=pzx50fvs523|width=100%|height=500px}} | ||
Im nachfolgenden Applet kannst du die Werte für a und b mithilfe der Schieberegler verändern. Beschreibe, wie jeweils die Werte der beiden Terme berechnet werden. <br> | Im nachfolgenden Applet kannst du die Werte für a und b mithilfe der Schieberegler verändern. Beschreibe, wie jeweils die Werte der beiden Terme berechnet werden. <br> | ||
Originallink https://www.geogebra.org/m/twss59dq | |||
<ggb_applet id="twss59dq" width="1200" height="909" border="888888" /><br> | <ggb_applet id="twss59dq" width="1200" height="909" border="888888" /><br> | ||
| Zeile 205: | Zeile 208: | ||
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme. | Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme. | ||
Originallink: https://www.geogebra.org/m/sbkxfzpa | |||
<ggb_applet id="ckxskbby" width="798" height="526" border="888888" /> | |||
<small>Applet des FLINK-Teams</small> | |||
<br /> | <br /> | ||
{{Box|Übung 7|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-aufstellen.shtml '''Aufgabenfuchs'''] die Aufgaben | {{Box|Übung 7|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-aufstellen.shtml '''Aufgabenfuchs'''] die Aufgaben | ||
| Zeile 319: | Zeile 324: | ||
In allen Anwendungsbereichen ist es wichtig, dass du den Text '''genau liest''', dir die Situation vorstellst und mit eigenen Worten beschreibst. | In allen Anwendungsbereichen ist es wichtig, dass du den Text '''genau liest''', dir die Situation vorstellst und mit eigenen Worten beschreibst. | ||
Originallink https://www.geogebra.org/m/yyah3gud<br> | |||
<ggb_applet id="neajewdb" width="812" height="562" border="888888" /> | |||
<small>Applet des FLINK-Teams</small> | |||
{{Box|Übung 12|Löse die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-aufstellen.shtml '''Aufgabenfuchs'''] | {{Box|Übung 12|Löse die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-aufstellen.shtml '''Aufgabenfuchs'''] | ||
* | * 14 | ||
Löse anschließend die LearningApps.|Üben}}<br> | |||
{{LearningApp|app=ppkrnf4tv20|width=100%|height=600px}} | {{LearningApp|app=ppkrnf4tv20|width=100%|height=600px}} | ||
{{LearningApp|app=p1sh1t89j20|width=100%|heigth=400px}} | {{LearningApp|app=p1sh1t89j20|width=100%|heigth=400px}} | ||
{{LearningApp|app=pgdsubmh223|width=100%| | {{LearningApp|app=pgdsubmh223|width=100%|height=400px}} | ||
<br> | <br> | ||
{{Box|Übung 13|Löse aus dem Buch die nachfolgenden Aufgaben. Notiere wie folgt im Heft:<br><br> | {{Box|Übung 13|Löse aus dem Buch die nachfolgenden Aufgaben. Notiere wie folgt im Heft:<br><br> | ||
| Zeile 347: | Zeile 355: | ||
'''b)''' Alter der Mutter: '''3y''' <br> | '''b)''' Alter der Mutter: '''3y''' <br> | ||
'''c)''' x steht für die Anzahl der Goldorfen, also Anzahl der Goldfische: '''x + 4''' <br> | '''c)''' x steht für die Anzahl der Goldorfen, also Anzahl der Goldfische: '''x + 4''' <br> | ||
'''d)''' a steht für den Preis eines Heftes und b steht für den Preis eines Umschlags, also: '''4a + | '''d)''' a steht für den Preis eines Heftes und b steht für den Preis eines Umschlags, also: '''4a + 5b = 6 [€]'''|2=Lösung zu S. 109 Nr. 2|3=Verbergen}} | ||
===1.4 Folgen beschreiben=== | |||
<br><small>Die nachfolgende Aufgabe wurde der Seite https://unterrichten.zum.de/wiki/Vera_8_interaktiv/Mathematik/Test_C entnommen. Sie wurde unter der Lizenz CC BY SA veröffentlicht. (Die Bilder wurden von Buss-Haskert geändert)</small> | <br><small>Die nachfolgende Aufgabe wurde der Seite https://unterrichten.zum.de/wiki/Vera_8_interaktiv/Mathematik/Test_C entnommen. Sie wurde unter der Lizenz CC BY SA veröffentlicht. (Die Bilder wurden von Buss-Haskert geändert)</small> | ||
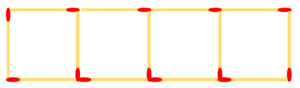
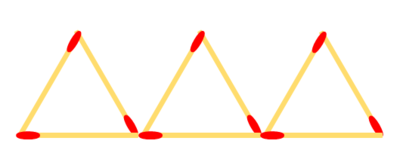
{{Box|Übung 14 - Streichholzketten 1|Mit Streichhölzern kann man Ketten mit Quadraten legen. | {{Box|Übung 14 - Streichholzketten 1|Mit Streichhölzern kann man Ketten mit Quadraten legen. | ||
[[Datei:Streichholzkette 1.png|rahmenlos]]|Üben}} | [[Datei:Streichholzkette 1.png|rahmenlos]]|Üben}} | ||
| Zeile 399: | Zeile 410: | ||
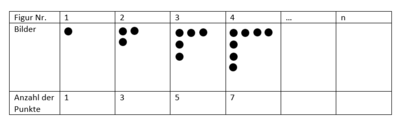
c) Gib einen Term an, mit dem du die Punkte an der n. Stelle berechnen kannst.|Üben}} | c) Gib einen Term an, mit dem du die Punkte an der n. Stelle berechnen kannst.|Üben}} | ||
{{Box|Übung 18 - Aufgaben | {{Box|Übung 18 - Aufgaben selbst entwickeln|[[Datei:Aufgaben selbst entwickeln 1.png|rahmenlos|700x700px]]|Üben}} | ||
{{Fortsetzung|weiter=2) Terme vereinfachen|weiterlink=Benutzer:Buss-Haskert/Terme/Terme vereinfachen}} | {{Fortsetzung|weiter=2) Terme vereinfachen|weiterlink=Benutzer:Buss-Haskert/Terme/Terme vereinfachen}} | ||
Aktuelle Version vom 25. Februar 2024, 09:30 Uhr
Neue Idee (12/2022): Buch des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/y87ytrk9
1) Variablen und Terme
Schreibe nur eine einzige Rechnung auf.
Beispiel: 4 Erwachsene und 2 Kinder
= 48 + 19
= 67 [€]
Bei den Schulklassen bezahlt immer nur eine erwachsene Person, denn die andere Begleitperson hat ja freien Eintritt.
Also gilt:
1.1 Was sind Variablen? Was sind Terme?
Entscheide, ob es sich um eine Variable, einen Term oder keins von beidem handelt:
Originallink: https://www.geogebra.org/m/svqmvxnp

Applet des FLINK-Teams
Anmerkung: Malpunkte zwischen einer Zahl und einer Variablen sind überflüssig und werden daher oft weggelassen.
3∙x = 3x
1∙a = 1a = a
-1a = -a
aber: 3∙5 35! (Hier muss der Malpunkt geschrieben werden!)
Du hast im Einstiegsbeispiel Eintrittspreise für den Zoobesuch berechnet. Stelle nun einen Term für die Berechnung des Eintrittspreises für Familien auf. Die Variable x soll dabei den Platz für die Anzahl der Erwachsenen freihalten, die Variable y den für die Anzahl der Kinder.
Im Einstiegsbeispiel beträgt der Eintrittspreis für die Erwachsenen immer 12,00 €. x Erwachsene müssen also x∙12,00 € bezahlen.
Der Preis für die Kinder beträgt immer 9,50 €, also bezahlen y Kinder y∙9,50 € Eintritt.
Insgesamt beträgt der Eintrittspreis für x Erwachsene und y Kinder also
x∙12,00 + y∙9,50 [€]
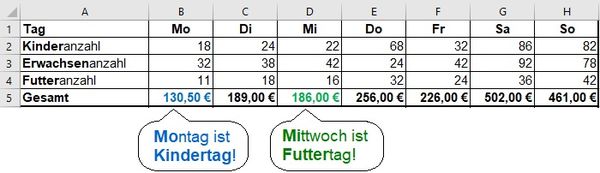
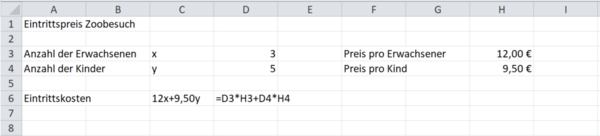
Eine Tabellenkalkulation könnte z.B. wie folgt aussehen:
(Hier kannst du auch den Preis pro Person anpassen)
1.2 Werte von Termen berechnen
Originallink: https://www.geogebra.org/m/n6cttesM
von Beraterinnen und Beratern für Unterrichtsentwicklung Mathematik
Beispiele:
5∙7 = 35
4 ∙2 - 10 |Punkt-vor Strich
= 8 - 10
Im nachfolgenden Applet kannst du die Werte für a und b mithilfe der Schieberegler verändern. Beschreibe, wie jeweils die Werte der beiden Terme berechnet werden.
Originallink https://www.geogebra.org/m/twss59dq

Haben die Terme 3a + 4b und 7ab immer denselben Wert? Begründe.
Erinnerung: Du multiplizierst einen Bruch mit einer Zahl, indem du den Zähler mit der Zahl multiplizierst und den Nenner beibehältst:
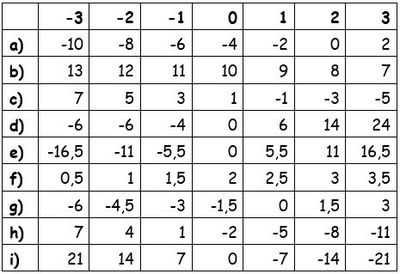
a) 51
b) 84
c) 17
d) 5
e)
f) 0
g) 24
h) 20
a) 13
b) 13
c) 22
d) 0
e) 0
Hier findest du die Lösungen. Schaue nach, ob deine Ergebnisse richtig sind und rechne bei falschen Ergebnissen die Aufgabe noch einmal neu - dann auf jeden Fall mit Angabe des Rechenwegs!
a) 1
b) -36
c) -7
d) -12
e) 17
f) 17
Zur automatischen Berechnung des Gesamtpreises muss in den Zellen B5 bis H5 jeweils eine Formel eingegeben werden! Es reicht nicht, einfach nur die vorher berechneten Werte einzugeben.
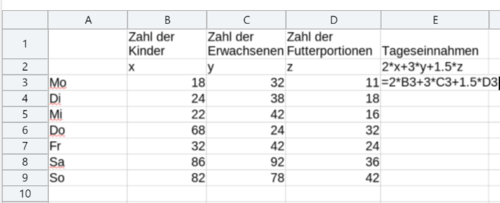
Wenn du alles richtig gemacht hast, müssten folgende Ergebnisse herauskommen (siehe Zeile 5).
1.3 Terme aufstellen
1.3.1 Terme aufstellen - Mathematische Texte
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
Beachte: Die Art des Terms wird immer nach der Rechnung benannt, die man zuletzt ausführen muss!
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme. Originallink: https://www.geogebra.org/m/sbkxfzpa

Applet des FLINK-Teams
a) Das Vierfache einer Zahl ODER Multipliziere eine Zahl mit 4 ODER...
b) Subtrahiere von 17 eine Zahl ODER Die Differenz aus 17 und einer Zahl ODER ...
c) Subtrahiere 10 vom Dreifachen einer Zahl ODER Die Differenz aus dem Dreifachen einer Zahl und 10 ODER ...
d) Dividiere eine Zahl durch 3 und subtrahiere 10 ODER Subtrahiere vom Quotienten aus einer Zahl und 3 die Zahl 10 ODER ...
e) Die Summe aus 3 und dem Fünffachen einer Zahl ODER Addiere das Fünffache einer Zahl zu 3 ODER ...
a) 15 - 9
b) 4 · 17
c) 34 - 11
d) 85 : 17
e) 7 + 2 · 7
Prüfe deine Lösungen zu S. 99 Nr. 2 und S. 100 Nr. 6 mithilfe der LearningApps:
1.3.2 Terme aufstellen - Geometrische Situationen
| Quadrat | u = 4·a | A = a² | ||
| Rechteck | u = 2a + 2b | A = a·b | ||
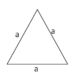
| gleichschenkliges Dreieck | u = 2a + c | 2 gleich lange Seiten | α+β+γ=180° | |
| gleichseitiges Dreieck | u = 3a | 3 gleich lange Seiten | α+β+γ=180° |
Hier findet du nur die Lösungsterme. Denke daran, dass bei dir im Heft auch die Bedeutung der Variablen stehen muss!
Schaue nach, ob deine Ergebnisse richtig sind. Korrigiere sie gegebenenfalls und ergänze die vereinfachten Terme.
a) u = x + y + y = x + 2y
b) u = x + y + x + y = 2x + 2y
Hier findest du die Lösungen.
Würfel (Kantenmodell oben): 12 ∙ x
Doppeltetraeder (Kantenmodell zweite Reihe links): 9 ∙ x
Oktaeder (Kantenmodell zweite Reihe rechts): 12 ∙ x
Würfel mit aufgesetzter Pyramide (Kantenmodell dritte Reihe links): 12 ∙ x + 4 ∙ y
a) Bedeutung der Variablen: x ist die Länge eines Teilstücks
Term: 5 ∙ x
b) Bedeutung der Variablen: y ist die Gesamtlänge
Term: y : 4
Ab hier findet du nur noch die Lösungsterme. Denke daran, dass bei dir im Heft auch die Bedeutung der Variablen stehen muss!
c) Term: m + n + n + m + n = 2 ∙ m + 3 ∙ n
Hier stehen immer nur die Lösungsterme. Denke daran, dass bei dir im Heft auch die Bedeutung der Variablen stehen muss!
Umfang Figur A: u = a + a + a + a ODER u = 4a
Umfang Figur B: u = a + a + b ODER u = 2a + b
Umfang Figur C: u = a + b + a + b + a + b + a + b ODER u = 4a + 4b
a) Umfang = 2 ∙ x + 3 ∙ x + 2 ∙ x + 3 ∙ x = (2x + 3x) ∙ 2 = 10x
Und eine App für Profis:
1.3.3 Terme aufstellen - Sachsituationen
In allen Anwendungsbereichen ist es wichtig, dass du den Text genau liest, dir die Situation vorstellst und mit eigenen Worten beschreibst.
Originallink https://www.geogebra.org/m/yyah3gud

Applet des FLINK-Teams
Eine mögliche Lösung zu a) ist
a) 2 ∙ y - 30; y steht für das Gewicht
b) c : 4; c steht für den ganzen Kuchen
a) x steht für die Teilnehmerzahl; 3€ ∙ x + 25€
a) Anzahl der Jungen: n
b) Alter der Mutter: 3y
c) x steht für die Anzahl der Goldorfen, also Anzahl der Goldfische: x + 4
1.4 Folgen beschreiben
Die nachfolgende Aufgabe wurde der Seite https://unterrichten.zum.de/wiki/Vera_8_interaktiv/Mathematik/Test_C entnommen. Sie wurde unter der Lizenz CC BY SA veröffentlicht. (Die Bilder wurden von Buss-Haskert geändert)
a) Übertrage die Tabelle in dein Heft. Schreibe jeweils die Anzahl der benötigten Streichhölzer in die freien Kästchen.
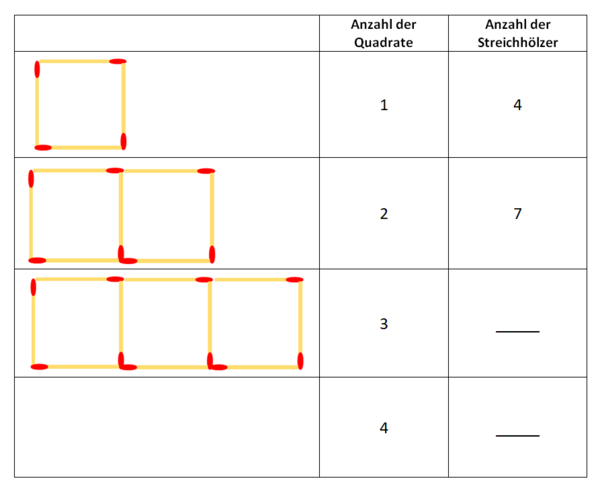
- bei 3 Quadraten 10 Streichhölzer und bei 4 Quadraten 13 Streichhölzer
b) Streichholzkette
Wie viele Streichhölzer werden für 12 solche Quadrate benötigt? Kreuze die richtige Antwort an.
(!23) (!24) (!36) (37) (!48)
c) Streichholzkette
Gib eine Gleichung an, die den Zusammenhang zwischen der Anzahl k der Quadrate und der Anzahl s der benötigten Streichhölzer allgemein beschreibt.
- z.B.: s = 3k + 1
Für die 2. Möglichkeit könnte eine LearningApp wie folgt aussehen: