Benutzer:L.hodankov/Lineare Funktionen untersuchen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Inhalte übernommen) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 47: | Zeile 47: | ||
</div> | </div> | ||
{{Box|Übung 3: Steigende und fallende Geraden|Bearbeite die nachfolgenden Apps, um dein Wissen über steigende und fallende Geraden und die Bedeutung von m in der Funktionsgleichung zu überprüfen.|Üben}} | |||
{{LearningApp|app=pcwv0txpt20|width=100%|height=400px}} | |||
{{h5p-zum|id=14434|height=300}} | |||
<br> | |||
{{Box|1=Übung 4|2=Erfinde Aufgaben für deinen Sitznachbarn in der Art:<br> | |||
"Nenne mir eine proportionale Funktion, deren Graph <span style="color:green">flach</span> <span style="color:red">fällt</span>." Lösung z.B. f(x) = <span style="color:red">'''-'''</span>[[Datei:Einhalb grün.png|rahmenlos|30x30px]]x. | |||
Prüft die Antworten mit GeoGebra.|3=Meinung}} | |||
<br> | |||
{{Lösung versteckt|Öffne die App GeoGebra und gib die Funktionsgleichung ein. Der zugehörige Graph wird sofort angezeigt. Steigt oder fällt dieser, steil oder flach?<br> | |||
[[Datei:GeoGebra Graphen zeichnen 1.png|rahmenlos|500x500px]]<br> | |||
[[Datei:GeoGebra Graphen zeichnen f(x) = 2x.png|rahmenlos|646x646px]]|Wie kann ich mit GeoGebra meine Antworten prüfen?|Verbergen}} | |||
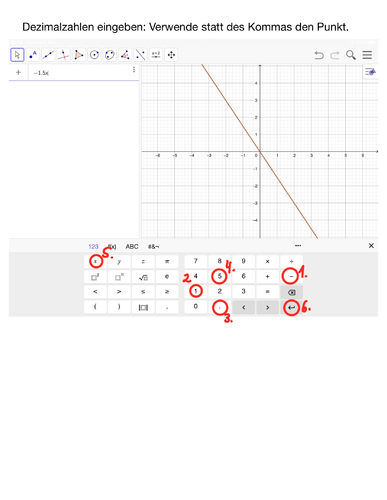
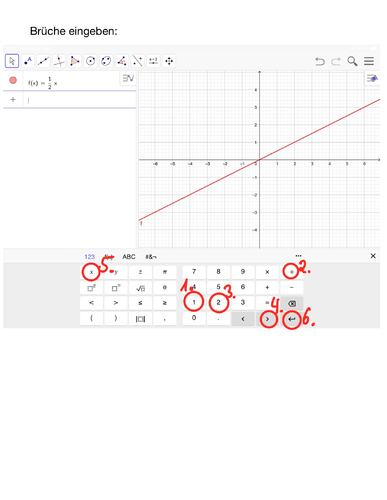
{{Lösung versteckt|[[Datei:GeoGebra Graphen zeichnen Dezimalzahlen f(x) = -1,5x.png|rahmenlos|500x500px]]<br> | |||
[[Datei:GeoGebra Graphen zeichnen Brüche f(x) = einhalb x.png|rahmenlos|500x500px]]|Dezimalzahlen oder Brüche bei GeoGebra eingeben|Verbergen}} | |||
<br> | |||
Teste dein Wissen mit einem '''Kahoot''' (im Unterricht). | |||
Version vom 22. August 2023, 18:41 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub . Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
SEITE IM AUFBAU !!!
Funktionsgleichung und Funktionsgraph
f(x) = mx + b Bedeutung von m und b für den Funktionsgraphen
Damit du einen Eindruck von der Bedeutung der Parameter m (Steigung) und b (y-Achsenabschnitt) der Funktionsgleichung linearer Funktionen f(x) = mx + b erhältst, verändere in der folgenden Animation mithilfe der Schieberegler die Größe von m und b. Notiere deine Beobachtungen stichpunktartig.

In der Funktionsgleichung linearer Funktionen f(x)= m·x + b haben die Parameter m und b verschiedene Bedeutungen:
b ist der y-Achsenabschnitt, im Punkt P(0|b) schneidet die Gerade die y-Achse.
Nun schauen wir uns die Steigung m genauer an. Dazu wählen wir den y-Achsenabschnitt b = 0, die Gerade geht also durch den Ursprung (0|0).
Erinnerung: Diese Funktionen heißen "proportionale Funktionen", da ihr Graph eine Ursprungsgerade ist.
Die Steigung m
Anschaulich vorstellen kannst du dir, dass die Funktion steigt, wenn der Wanderer den Berg hochsteigen muss.
Fällt die Funktion, "fällt" der Wanderer bergab.
Um zu unterscheiden, ob eine Gerade steil oder flach verläuft (steigt oder fällt), beobachte in der nächsten Simulation den Maulwurf, der seinen Maulwurfshügel hinaufklettert.

Wenn die Steigung m steil ist, muss der Maulwurf sehr mutig sein!
Fülle den nachfolgenden Lückentext aus und übertrage ihn in deine Mappe (Goodnotes):
Die Steigung m einer proportionalen (linearen) Funktion f(x) = mx bestimmt den Verlauf der Geraden:
Für m > 0 steigt die Gerade und für m < 0 fällt die Gerade.
Die Gerade steigt flach für 0 < m < 1 und steil für m > 1.
Die Gerade fällt flach für -1 < m < 0 und steil für m < -1.
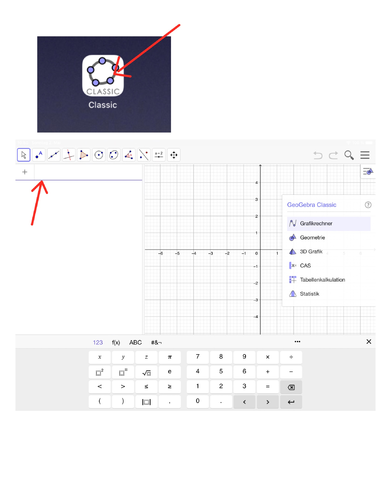
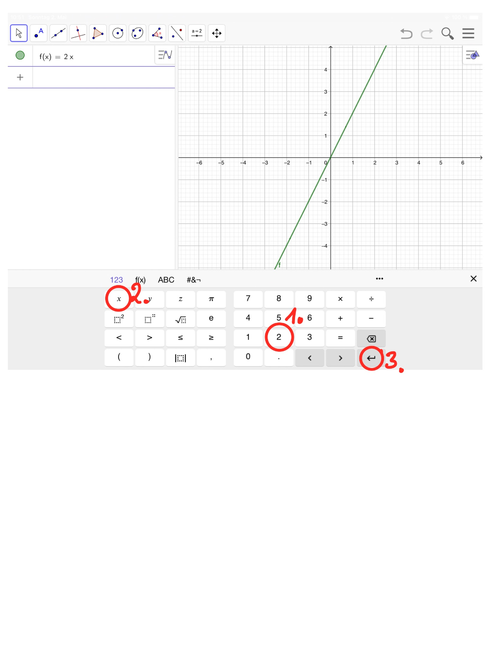
Öffne die App GeoGebra und gib die Funktionsgleichung ein. Der zugehörige Graph wird sofort angezeigt. Steigt oder fällt dieser, steil oder flach?
Teste dein Wissen mit einem Kahoot (im Unterricht).