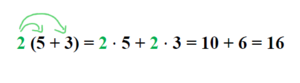Jule Volbers/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 250: | Zeile 250: | ||
{{Box|1 = Training: lineare Gleichungen lösen |2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. | {{Box|1 = Training: lineare Gleichungen lösen |2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. Trage die Ergebnisse in die Box zur Aufgabe in deinem Begleitmaterial ein. | ||
'''a)''' <math>2a-64=5+a</math> | '''a)''' <math>2a-64=5+a</math> | ||
| Zeile 368: | Zeile 368: | ||
{{Box|1 = Einfache quadratische Gleichungen|2= | {{Box|1 = Einfache quadratische Gleichungen|2= | ||
Löse die quadratischen Gleichungen '''ohne p-q-Formel'''. | Löse die quadratischen Gleichungen '''ohne p-q-Formel'''. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung. | ||
a) <math>0=x^2-64</math> | a) <math>0=x^2-64</math> | ||
| Zeile 420: | Zeile 420: | ||
{{Box|1=Quadratische Gleichungen mit p-q-Formel| 2 = Löse die quadratischen Gleichungen. Nutze hierfür den Kasten zur Aufgabe in deinem Begleitmaterial. Kontrolliere deine Lösung. | |||
{{Box|1= | |||
Löse die quadratischen Gleichungen. | |||
a) <math>0=x^2+12x+27</math> | a) <math>0=x^2+12x+27</math> | ||
| Zeile 514: | Zeile 463: | ||
\end{alignat} | \end{alignat} | ||
</math>|2=Lösung anzeigen|3=Lösung ausblenden}} | </math>|2=Lösung anzeigen|3=Lösung ausblenden}} | ||
|3 = Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
=='''Vernetzte Aufgaben '''== | |||
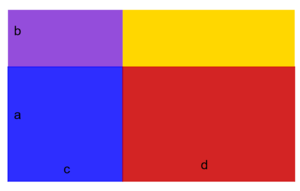
{{Box|1 = Flächeninhalt |2= Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben. | |||
{{Box|1= | |||
Klicke alle Terme an, die den Flächeninhalt der Fläche beschreiben. | |||
{{LearningApp|app=pxj3hfqot18|width=100%|height=400px}} | {{LearningApp|app=pxj3hfqot18|width=100%|height=400px}} | ||
| Zeile 528: | Zeile 478: | ||
{{Lösung versteckt|1=Mache dir bewusst, welche Bedeutung die einzelnen Glieder der Terme haben.|2=Tipp 2|3=schließen}} | {{Lösung versteckt|1=Mache dir bewusst, welche Bedeutung die einzelnen Glieder der Terme haben.|2=Tipp 2|3=schließen}} | ||
{{Lösung versteckt|1=Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.|2=Tipp 3|3=schließen}} | {{Lösung versteckt|1=Zeichne die Rechtecke, die durch die einzelnen Term-Glieder repräsentiert werden, in dein Heft und überprüfe, ob sich daraus die Figur zusammen setzen lässt.|2=Tipp 3|3=schließen}} | ||
| | |Üben|Farbe={{Farbe|orange|heller}}}} | ||
Version vom 21. März 2023, 07:21 Uhr
Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen.
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
Klammern in Termen
Klammern auflösen: Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.
Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
3. Gleichungen
Lineare Gleichungen lösen
Quadratische Gleichungen lösen. Auch für die Lösung quadratischer Gleichungen hast du Verfahren kennengelernt. Die Aufgaben helfen dir dabei, diese zu wiederholen.