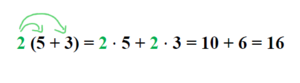Jule Volbers/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 235: | Zeile 235: | ||
{{Box | 1= | {{Box | 1=Training: lineare Gleichungen lösen| | ||
2= | 2= Löse die Gleichungen. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt. | ||
'''b)''' <math>a-64=5</math> | '''b)''' <math>a-64=5</math> | ||
| Zeile 300: | Zeile 254: | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
''' | '''a)''' <math>3x+7=16</math> | ||
{{Lösung versteckt|1=<math>\begin{align} & & 3x+7&=16 & &\mid -7\\ | {{Lösung versteckt|1=<math>\begin{align} & & 3x+7&=16 & &\mid -7\\ | ||
\Leftrightarrow & & 3x &=9 & &\mid :3\\ | \Leftrightarrow & & 3x &=9 & &\mid :3\\ | ||
| Zeile 315: | Zeile 268: | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
''' | '''b)''' <math>4(x+1)-4x-5=1</math> | ||
{{Lösung versteckt|1=<math>\begin{align} & & 4(x+1)-4x-5 &=1\\ | {{Lösung versteckt|1=<math>\begin{align} & & 4(x+1)-4x-5 &=1\\ | ||
\Leftrightarrow & & 4x+4-4x-5 &=1\\ | \Leftrightarrow & & 4x+4-4x-5 &=1\\ | ||
| Zeile 366: | Zeile 296: | ||
\end{align}</math> | \end{align}</math> | ||
|2=Lösung|3=Lösung ausblenden}} | |2=Lösung|3=Lösung ausblenden}} | ||
'''b)''' <math>d\cdot (d-5)=0</math> | |||
{{Lösung versteckt|1=Überlege dir, was für zwei Faktoren gilt, deren Produkt <math>0</math> ist.|2=Tipp |3=Tipp ausblenden}} | |||
{{Lösung versteckt|1=Ein Produkt ist dann <math>0</math>, wenn einer der Faktoren <math>0</math> ist. Deshalb kann man die Aufgabe so lösen: | |||
<math>\begin{align} & & d\cdot (d-5)&=0\\ | |||
\Leftrightarrow & & d=0 &\text{ oder } d-5=0\\ | |||
\Leftrightarrow & & d=0 &\text{ oder } d=5\\ | |||
& & \mathbb{L}=\{0,5\} | |||
\end{align}</math> | |||
Probe: | |||
<math>\begin{align} & & 0\cdot (0-5)&=0\\ | |||
\Leftrightarrow & & 0&=0 | |||
\end{align}</math> | |||
<math>\begin{align} & & 5\cdot (5-5)&=0\\ | |||
\Leftrightarrow & & 5\cdot 0&=0\\ | |||
\Leftrightarrow & & 0&=0 | |||
\end{align}</math> | |||
|2=Lösung|3=Lösung ausblenden}} | |||
'''g)''' <math>\frac{3}{z+1}=-\frac{5}{2z-1}</math> | '''g)''' <math>\frac{3}{z+1}=-\frac{5}{2z-1}</math> | ||
Version vom 20. März 2023, 17:35 Uhr
Willkommen auf dem Lernpfad: Nützliche Werkzeuge - Terme und Gleichungen.
In diesem Lernpfad geht es um das Vertiefen deines Wissens über Terme, Variablen und Gleichungen.
Du findest hier eine Wiederholung zu den Begriffen und Übungsaufgaben zu den Themen Terme aufstellen, Terme umformen und Gleichungen lösen. .
1.Terme, Variablen und Gleichungen
2.Terme
Terme aufstellen
Terme vereinfachen
Klammern in Termen
Klammern auflösen: Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen.
Ausklammern Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
3. Gleichungen
Lineare Gleichungen lösen
Quadratische Gleichungen lösen