Anton-Philipp-Reclam-Gymnasium Leipzig/Kraefte725/Kräfte an der Schraubenfeder: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
<big> | <big>Hooke’ sches Gesetz und Federkraft</big> | ||
<u>Definition ( Federkraft)</u> | <u>Definition ( Federkraft)</u> | ||
| Zeile 29: | Zeile 29: | ||
<big>Was ist das | <big>Was ist das Hooke’ sches Gesetz :</big><br /> | ||
Definition: | Definition: | ||
Das Hookesche Gesetz beschreibt die Wirkung auf Körper die ihre Länge gleichmäßig ändern (nur linear elastische Körper z.B. Schraubenfeder ) , durch die Belastung einer Kraft F ,die nach Ende der Belastung wieder in ihre ursprüngliche Form zurück kehrt . | Das Hookesche Gesetz beschreibt die Wirkung auf Körper die ihre Länge gleichmäßig ändern (nur linear elastische Körper z.B. Schraubenfeder ), durch die Belastung einer Kraft F, die nach Ende der Belastung wieder in ihre ursprüngliche Form zurück kehrt . | ||
<u>Übung:</u> | |||
<br /> | <br /> | ||
Version vom 11. Januar 2023, 10:19 Uhr
Hooke’ sches Gesetz und Federkraft
Definition ( Federkraft)
Die Federkraft drückt aus wie stark sich ein elastischer Körper verformen kann wenn eine Kraft auf ihn einwirkt. Die Verlängerung (Dehnung) des elastischen Körper ‘s ist hierbei proportional.
Berechnung
Die Federkraft lässt sich mit der Formel F = – D • s Berechnen. F ist die Federkraft. Diese wird in der Einheit Newton (N) angegeben.
Die Federkonstante lässt sich mit der Formel D = Fs Berechnen. D beschreibt die Federkonstante (wie weich/ hart die Feder ist, Eigenschaften) in der Einheit Newton pro Meter ( )
Die Längenänderung lässt sich mit der Formel s = FD Berechnen. Dies wird in cm angegeben.
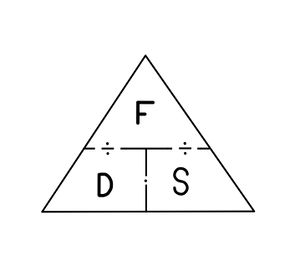
Merkedreieck:
Was ist das Hooke’ sches Gesetz :
Definition:
Das Hookesche Gesetz beschreibt die Wirkung auf Körper die ihre Länge gleichmäßig ändern (nur linear elastische Körper z.B. Schraubenfeder ), durch die Belastung einer Kraft F, die nach Ende der Belastung wieder in ihre ursprüngliche Form zurück kehrt .
Übung: