Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 2: Zeile 2:


===Zuordnungen===
===Zuordnungen===
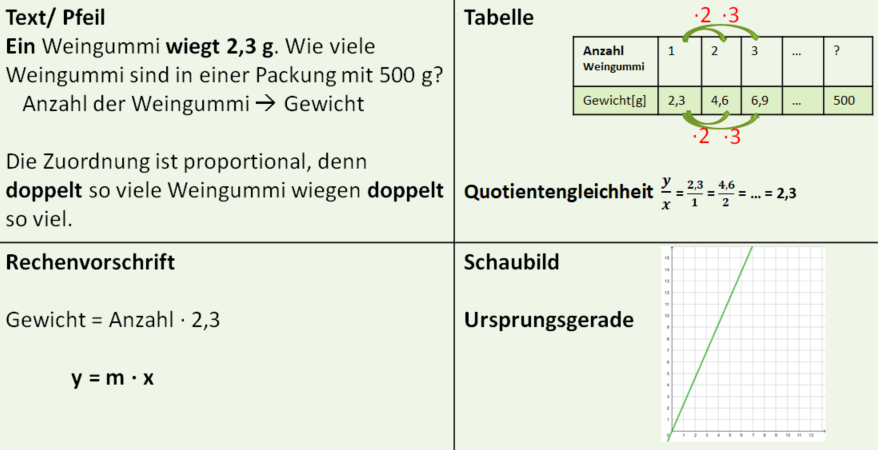
Du hast in Klasse 7 proportionale und umgekehrt proportionale (antiproportionale) Zuordnungen kennengelernt.{{Box|1=Eigenschaften proportionaler Zuordnungen|2=Eine proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße das '''Doppelte''' (Dreifache…) der Ausgabegröße gehört.
Du hast in Klasse 7 proportionale und umgekehrt proportionale (antiproportionale) Zuordnungen kennengelernt.
 
==== Proportionale Zuordnungen und Dreisatz ====
 
{{Box|1=Eigenschaften proportionaler Zuordnungen|2=Eine proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße das '''Doppelte''' (Dreifache…) der Ausgabegröße gehört.


Für jedes Wertepaar in der '''Wertetabelle''' gilt '''Quotientengleichheit''':<br>
Für jedes Wertepaar in der '''Wertetabelle''' gilt '''Quotientengleichheit''':<br>
Zeile 12: Zeile 16:
Die '''Rechenvorschrift''' lautet: Gewicht = 2,3·Anzahl der Weingummi.|3=Merksatz}}[[Datei:Proportionale_Zuordnung_Darstellungen_(Weingummi).png|rahmenlos|884x884px]]
Die '''Rechenvorschrift''' lautet: Gewicht = 2,3·Anzahl der Weingummi.|3=Merksatz}}[[Datei:Proportionale_Zuordnung_Darstellungen_(Weingummi).png|rahmenlos|884x884px]]


Zusammenfassung:{{#ev:youtube|MT3hVo_BfT0|600|center}}
{{#ev:youtube|MT3hVo_BfT0|600|center}}


{{Box|Dreisatz bei proportionalen Zuordnungen|Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden.[[Datei:Dreisatz schrittweises Vorgehen p kurz.png|ohne|700x700px]]|Merksatz}}
{{Box|Dreisatz bei proportionalen Zuordnungen|Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden.[[Datei:Dreisatz schrittweises Vorgehen p kurz.png|ohne|700x700px]]|Merksatz}}
Zeile 18: Zeile 22:
{{#ev:youtube|M6--2jhtrKM|800|center}}
{{#ev:youtube|M6--2jhtrKM|800|center}}


==== Umgekehrt proportionale (antiproportionale) Zuordnungen ====


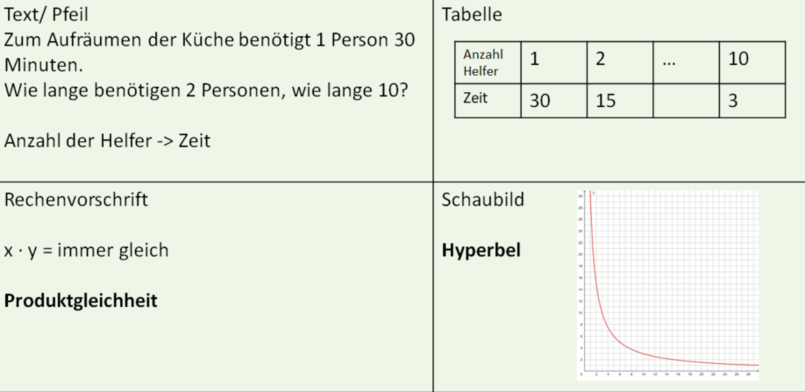
{{Box|1=Eigenschaften umgekehrt proportionaler Zuordnungen (antiproportional)|2=Eine umgekehrt proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße die '''Hälfte''' (Drittel...) der Ausgabegröße gehört.
{{Box|1=Eigenschaften umgekehrt proportionaler Zuordnungen (antiproportional)|2=Eine umgekehrt proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße die '''Hälfte''' (Drittel...) der Ausgabegröße gehört.
Zeile 38: Zeile 43:


{{#ev:youtube|izN8-f70q2s|800|center}}
{{#ev:youtube|izN8-f70q2s|800|center}}
{{Box|Übung Zuordnungen|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch.
* S.144, Nr.1-8|Üben}}
=== Prozentrechnung ===

Version vom 29. Dezember 2022, 18:37 Uhr

Kapitel 3: Zuordnungen, Prozent-und Zinsrechnung

Zuordnungen

Du hast in Klasse 7 proportionale und umgekehrt proportionale (antiproportionale) Zuordnungen kennengelernt.

Proportionale Zuordnungen und Dreisatz

Eigenschaften proportionaler Zuordnungen

Eine proportionale Zuordnung liegt vor, wenn zum Doppelten (Dreifachen,…) der Eingabegröße das Doppelte (Dreifache…) der Ausgabegröße gehört.

Für jedes Wertepaar in der Wertetabelle gilt Quotientengleichheit:
= y : x = 2,3 : 1= 4,6 : 2 = 6,9 : 3 = … = 2,3 (Jedes Weingummi ist gleich schwer und wiegt 2,3 g).

Für das Schaubild gilt: Alle Punkte einer proportionalen Zuordnung liegen auf einer Geraden durch den Ursprung, also durch den Punkt (0I0).

Die Rechenvorschrift lautet: Gewicht = 2,3·Anzahl der Weingummi.

Proportionale Zuordnung Darstellungen (Weingummi).png

Video laden
YouTube


Dreisatz bei proportionalen Zuordnungen
Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem Dreisatz (3 Schritte) berechnet werden.
Datei:Dreisatz schrittweises Vorgehen p kurz.png
Video laden
YouTube

Umgekehrt proportionale (antiproportionale) Zuordnungen

Eigenschaften umgekehrt proportionaler Zuordnungen (antiproportional)

Eine umgekehrt proportionale Zuordnung liegt vor, wenn zum Doppelten (Dreifachen,…) der Eingabegröße die Hälfte (Drittel...) der Ausgabegröße gehört.

Für jedes Wertepaar in der Wertetabelle gilt Produktgleichheit:
y·x = 1·30 = 2·15 = 3·10 = … = 30 (Minuten).

Für das Schaubild gilt: Alle Punkte einer umgekehrt proportionalen Zuordnung liegen auf einer Kurve, die Hyperbel, heißt.

Die Rechenvorschrift lautet Zeit = 30 : Anzahl der Helfer, also y = 30 : x

Umgekehrt proportionale Zuordnung Darstellungsmöglichkeiten.png


Video laden
YouTube


Dreisatz bei umgekehrt proportionalen Zuordnungen

Bei einer umgekehrt proportionalen Zuordnung kann die gesuchte Größe mit dem Dreisatz (3 Schritte) berechnet werden.
Dreisatz up schrittweises Vorgehen kurz.png


Video laden
YouTube


Übung Zuordnungen

Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch.

  • S.144, Nr.1-8

Prozentrechnung

Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Vorbereitungskurs_ZP_10_Mathematik/Zuordnungen&oldid=72904“