Benutzer:Buss-Haskert/Trigonometrie/Sinus,Kosinus,Tangens: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 40: | Zeile 40: | ||
Das Seitenverhältnis hängt nicht von der Größe der Dreiecke ab, sondern nur vom Winkel α. <br> | Das Seitenverhältnis hängt nicht von der Größe der Dreiecke ab, sondern nur vom Winkel α. <br> | ||
<br><br> | <br><br> | ||
Bewege die Punkte B<sub>1</sub>, B<sub>2</sub> und C<sub>1</sub | Bewege die Punkte B<sub>1</sub>, B<sub>2</sub> und C<sub>1</sub> und beobachte die Seitenverhältnisse. | ||
<ggb_applet id="zanbxdhr" width="1692" height="824" border="888888" /> | <ggb_applet id="zanbxdhr" width="1692" height="824" border="888888" /> | ||
<br><br> | <br><br> | ||
{{Box|Seitenverhältnisse in rechtwinkligen Dreiecken|In ähnlichen rechtwinkligen Dreiecken gilt:<br> | {{Box|Seitenverhältnisse in rechtwinkligen Dreiecken|In ähnlichen rechtwinkligen Dreiecken gilt:<br> | ||
Das Seitenverhältnis hängt nicht von der Größe der Dreiecke ab, sondern nur vom Winkel α.<br> | Das Seitenverhältnis hängt nicht von der Größe der Dreiecke ab, sondern nur vom Winkel α.<br> | ||
Diesen Zusammenhang zwischen Winkelgröße und Seitenlängen im rechtwinkligen Dreieck beschreiben die Winkelfunktionen Sinus, Kosinus und Tangens.|Merksatz}} | Diesen Zusammenhang zwischen Winkelgröße und Seitenlängen '''im rechtwinkligen Dreieck''' beschreiben die Winkelfunktionen '''Sinus''', '''Kosinus''' und '''Tangens'''.|Merksatz}} | ||
<br> | <br> | ||
Version vom 5. Januar 2021, 21:46 Uhr
==1) Sinus, Kosinus, Tangens - Seitenverhältnisse in rechtwinkligen Dreiecken==
1.1 Steigung einer Straße
Der Einstieg ist angelehnt an das Material des Landesbildungsservers BW https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/geometrie/trig/trigors/lernumgebung/index.html Es wurde unter der Lizenz CC BY veröffentlicht

Es gibt mehrere Möglichkeiten, die Steigung einer Straße anzugeben:
1. Angabe in Prozent
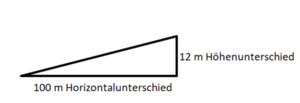
Das Verkehrsschild gibt die Steigung einer Straße in Prozent an.
a) Was bedeutet die Angabe von 12% Steigung? Erkläre!
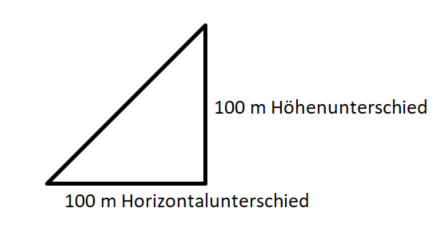
b) Gibt es eine Steigung, die größer als 100% ist?
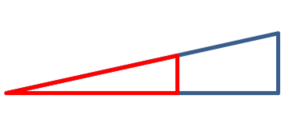
2. Angabe mithilfe des Steigungsdreiecks und m
Die Steigung einer Geraden f(x) = mx + b gibt der Faktor m an. Dazu zeichnest du das Steigungsdreieck.
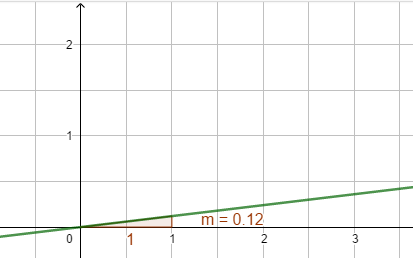
m = = 0,12
Boxmath>\alpha</math>
Das nachfolgende Applet zeigt diese drei Möglichkeiten noch einmal. Verändere die Steigung mithilfe des Schiebereglers und beobachte, was passiert.

Applet von holo2012
Versuche herauszufinden, welcher Zusammenhang zwischen den verschiedenen Darstellungsmöglichkeiten besteht.
1. Verändere die Höhe und beobachte die anderen Angaben zur Steigung.
2. Aktiviere das Kontrollkästchen "Steigung eines beliebigen Punktes auf der Straße" und verschiebe den Punkt P entlang der Straße.
Ergebnis: In den ähnlichen (rechtwinkligen) Dreiecken gilt:
Das Seitenverhältnis hängt nicht von der Größe der Dreiecke ab, sondern nur vom Winkel α.
Bewege die Punkte B1, B2 und C1 und beobachte die Seitenverhältnisse.

Materialsammlung: Übungen auf der Seite Aufgabenfuchs