Buss-Haskert/Potenzen

SEITE IM AUFBAU !!!

Lernpfad Potenzen: Sehr große und sehr kleine Zahlen

  
In diesem Lernpfad lernst du

• wie man mit Potenzen rechnet (Potenzgesetzte)
• wie man sehr große und sehr kleine Zahlen mit Potenzen schreibt
  

Bearbeite die Schritte des Lernpfades selbständig. Stelle Fragen, wo du unsicher bist. Achte auf die Zeit!!

Die Übungen im Buch beziehen sich auf das Schülerbuch "Schnittpunkt Mathematik 9 - Differenzierende Ausgabe" des Klett-Verlages.

Vorwissen

Bearbeite die Aufgaben in der Tabelle: (Buch: Schnittpunkt Mathematik - Differenzierende Ausgabe 9, Klett)

Ich kann ...	Buch S. 52	Übungen online
- Terme berechnen (Vorrangregeln)	Nr. 4
- Zahlen runden.	Nr. 2
- die Quadratzahlen auswendig.	Nr. 6
- Potenzen als Produkt schreiben und berechnen.	Nr. 3

Vergleiche deine Lösungen mit den Lösungen hinten im Buch!

1) Potenzen

Definition Potenzen

Einer Legende nach hat der indische Erfinder des Schachspiels dieses seinem Herrscher zum Geschenk gemacht. Also Belohnung wünschte er sich für das erste Feld 1 Reiskorn und für jedes weitere doppelt so viele Körner wie auf dem vorherigen.

Übertrage die nachfolgende Tabelle in dein Heft und fülle sie aus:

Feld	1	2	3	4	5	6	7	8	9	10	...	20	...
Anzahl der Reiskörner auf dem Feld	1	2	4	8
Anzahl in (Zweier-)Potenzen	20	21	22	23

Die Anzahl der Reiskörner pro Feld verdoppelt sich immer, wir rechnen: 1. Feld: 1
2. Feld: 2
3. Feld: 2∙2 = 4
4. Feld: 2∙2∙2 = 8
5. Feld: 2∙2∙2∙2 = 16
usw.
Die Produkte schreiben wir als Potenz:
1. Feld: 1
2. Feld: 2
3. Feld: 2∙2 = 2² = 4
4. Feld: 2∙2∙2 = 2³ = 8
5. Feld: 2∙2∙2∙2 = 2⁴ =16

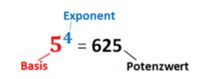
Ein Produkt aus gleichen Faktoren schreiben wir verkürzt als Potenz. Merke dir die nachfolgenden Begriffe!

Definition Potenz

Ein Produkt aus n gleichen Faktoren a kann man verkürzt als Potenz schreiben.
.
Beispiel:
5 · 5 · 5 · 5 = 5⁴ = 625

Merke a⁰ = 1; a¹ = a

Potenzen berechnen

Übung 1 (*)

Löse die nachfolgenden Apps zum Kopfrechnen mit Potenzen

Übung 2 (**)

Löse die folgenden Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung.

• S. 55 Nr. 7
• S. 55 Nr. 8
• S. 55 Nr. 9
• S. 55 Nr. 11

64 = 8² = 4³ = 2⁶

a) -2⁴ = -2·2·2·2 = -16, denn das Minuszeichen wird nicht mit potenziert.
2⁴ = 16
b) (-3)³ = (-3)·(-3)·(-3) = -27, denn hier wird auch das Minuszeichen mit potenziert, da es mit in der Klammer steht.

-3^Hochstellen = -3·3·3 = -27, hier wird das Minuszeichen nicht mit potenziert.

Übung 3 (***)

Löse die Anwendungsaufgabe. Achte auf eine vollständige und übersichtliche Darstellung.

• S. 55 Nr. 15
• S. 55 Nr. 16

Nach einer halben Stunde sind also 700·2 Keime vorhanden, nach einer weiteren halben Stunde 700·2·2 usw.Die Verdopplung geschieht jede halbe Stunde. Wie oft können sich die Keime dann in sechs Stunden verdoppeln?

Löse durch Probieren: 700·2^? = 1000000000 ? Nutze den Taschenrechner

Video zur wissenschaftlichen Schreibweise:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

2) Potenzgesetze