E-Learning Boxplot/Lernpfad E-Learning Boxplot: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 14: | Zeile 14: | ||
|- | |- | ||
|Anzahl | |Anzahl | ||
|5 | |5 | ||
|5 | |||
|4 | |||
|3 | |3 | ||
| | |4 | ||
|3 | |3 | ||
|} | |} | ||
| Zeile 85: | Zeile 85: | ||
|Anzahl | |Anzahl | ||
|0 | |0 | ||
|7 | |||
|6 | |6 | ||
| | |10 | ||
| | |1 | ||
|0 | |0 | ||
|} | |} | ||
| Zeile 129: | Zeile 129: | ||
|'''2''' | |'''2''' | ||
|'''2''' | |'''2''' | ||
|''' | |'''2''' | ||
|'''3''' | |'''3''' | ||
|'''3''' | |'''3''' | ||
| Zeile 146: | Zeile 146: | ||
|'''4''' | |'''4''' | ||
|'''4''' | |'''4''' | ||
| style="background:#FFFF00" |''' | | style="background:#FFFF00" |'''5''' | ||
|} | |} | ||
'''Minimum: 2''' | '''Minimum: 2''' | ||
'''Maximum: | '''Maximum: 5''' | ||
Somit beträgt die '''Spannweite | Somit beträgt die '''Spannweite 3''', denn die Differenz zwischen den Maximum (=5) und dem Minimum (=2) ist 3. | ||
Da die Noten von 24 SchülerInnen angegeben sind, haben die eine gerade Anzahl an Zahlenwerten. Um den Median zu bestimmen, nehmen also den Durchschnitt vom 12. und 13. Zahlenwert. | Da die Noten von 24 SchülerInnen angegeben sind, haben die eine gerade Anzahl an Zahlenwerten. Um den Median zu bestimmen, nehmen also den Durchschnitt vom 12. und 13. Zahlenwert. | ||
| Zeile 191: | Zeile 191: | ||
|'''2''' | |'''2''' | ||
|'''2''' | |'''2''' | ||
|''' | |'''2''' | ||
|'''3''' | |'''3''' | ||
|'''3''' | |'''3''' | ||
| Zeile 208: | Zeile 208: | ||
|'''4''' | |'''4''' | ||
|'''4''' | |'''4''' | ||
|''' | |'''5''' | ||
|} | |} | ||
| Zeile 250: | Zeile 250: | ||
| style="background:#B2DFEE" |'''2''' | | style="background:#B2DFEE" |'''2''' | ||
| style="background:#B2DFEE" |'''2''' | | style="background:#B2DFEE" |'''2''' | ||
| style="background:#B2DFEE" |''' | | style="background:#B2DFEE" |'''2''' | ||
| style="background:#B2DFEE" |'''3''' | | style="background:#B2DFEE" |'''3''' | ||
| style="background:#B2DFEE" |'''3''' | | style="background:#B2DFEE" |'''3''' | ||
| Zeile 267: | Zeile 267: | ||
| style="background:#CAFF70" |'''4''' | | style="background:#CAFF70" |'''4''' | ||
| style="background:#CAFF70" |'''4''' | | style="background:#CAFF70" |'''4''' | ||
| style="background:#CAFF70" |''' | | style="background:#CAFF70" |'''5''' | ||
|} | |} | ||
| Zeile 307: | Zeile 307: | ||
| style="background:#B2DFEE" |'''2''' | | style="background:#B2DFEE" |'''2''' | ||
| style="background:#00F5FF" |'''2''' | | style="background:#00F5FF" |'''2''' | ||
| style="background:#00F5FF" |''' | | style="background:#00F5FF" |'''2''' | ||
| style="background:#B2DFEE" |'''3''' | | style="background:#B2DFEE" |'''3''' | ||
| style="background:#B2DFEE" |'''3''' | | style="background:#B2DFEE" |'''3''' | ||
| Zeile 324: | Zeile 324: | ||
| style="background:#CAFF70" |'''4''' | | style="background:#CAFF70" |'''4''' | ||
| style="background:#CAFF70" |'''4''' | | style="background:#CAFF70" |'''4''' | ||
| style="background:#CAFF70" |''' | | style="background:#CAFF70" |'''5''' | ||
|} | |} | ||
Das '''erste Quartil liegt bei 2'''. Das '''dritte Quartil''' liegt bei '''4'''. | |||
Der '''Quartilsabstand''' liegt also ''' | Der '''Quartilsabstand''' liegt also bei '''2'''. | ||
Nun haben wir alle notwendigen Größen bestimmt und sind in der Lage, den zugehörigen Boxplot darzustellen. | Nun haben wir alle notwendigen Größen bestimmt und sind in der Lage, den zugehörigen Boxplot darzustellen. | ||
[[Datei:Boxplot | [[Datei:Boxplot GHR11B22.png]] | ||
Dies ist nun ein besonderer Boxplot, da sowohl das | Dies ist nun ein besonderer Boxplot, da sowohl das Minimum als auch das erste Quartil bei 2 liegen. Wie können wir den Boxplot nun deuten? | ||
====Deutung eines Boxplots==== | ====Deutung eines Boxplots==== | ||
Dem Boxplot können wir entnehmen, dass alle Noten zwischen 2 und | Dem Boxplot können wir entnehmen, dass alle Noten zwischen 2 und 5 liegen. Da der Median bei 3 liegt, hat die eine Hälfte der Klasse eine 3 oder eine bessere Note geschrieben, während die andere Hälfte der Klasse eine 3 oder eine schlechtete Note geschrieben hat. Dem ersten Quartil können wir entnehmen, dass ein Viertel der Klasse | ||
Wir haben an einem Beispiel gesehen, wie ein Boxplot erstellt wird. Die Aufgabe lautet nun einen Boxplot für die Biologiearbeit der Klasse GHR11A zu erstellen. | Wir haben an einem Beispiel gesehen, wie ein Boxplot erstellt wird. Die Aufgabe lautet nun einen Boxplot für die Biologiearbeit der Klasse GHR11A zu erstellen. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 349: | Zeile 349: | ||
|- | |- | ||
|Anzahl | |Anzahl | ||
|5 | |5 | ||
|5 | |||
|4 | |||
|3 | |3 | ||
| | |4 | ||
|3 | |3 | ||
|} | |} | ||
Version vom 19. November 2020, 20:29 Uhr
DIESE SEITE BEFINDET SICH NOCH IN DER ENTWICKLUNG
Die Situation
Die Klassen GHR11A und GHR11B haben eine Klassenarbeit im Fach Biologie geschrieben. Folgendermaßen sind die Klassenarbeiten ausgefallen:
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl | 5 | 5 | 4 | 3 | 4 | 3 |
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl | 0 | 7 | 6 | 10 | 1 | 0 |
Nun stellt sich die Lehrerin die Frage, welche der Klassen besser abgeschnitten hat. Sie ermittelt den Notendurschschnitt. Dieser liegt bei beiden Klassen bei 3,2. Somit stellt Sie zufrieden fest, dass beide Klassen gleich gut sind. Wie beurteilen Sie die Erkenntnis der Lehrerin? Sind Sie derselben Meinung?
Der Boxplot
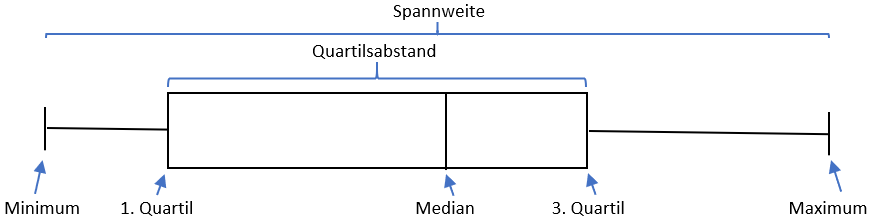
Ein Boxplot ist ein Diagramm zur graphischen Darstellung von Datensätzen. Als erstes lernen wir nun die Größen kennen, die in einem Boxplot abgebildet werden.
Minimum: Als Minimum wird der kleinste Wert in einem der Größe nach sortierten Datensatz bezeichnet.
Maximum: Als Maximum wird der größte Wert in einem der Größe nach sortierten Datensatz bezeichnet.
Spannweite: Als Spannweite wird der Abstand bzw. die Differenz zwischen dem Minimum und dem Maximum bezeichnet.
Median: Der Median (oder Zentralwert) teilt einen Datensatz in zwei gleichgroße Hälften ein: Die eine Hälfte der Daten ist höchstens so groß wie der Media, die andere Hälfte ist mindestens so groß. Er ist die Zahl, die bei der Größe nach geordneten Zahlenwerten in der Mitte liegt. Hier können nun zwei Fälle unterschieden werden:
- Ist die Anzahl der Zahlenwerte ungerade, dann wird die mittlere Zahl ausgewählt.
- Ist die Anzahl der Zahlenwerte gerade, dann wird der Durchschnitt der beiden mittleren Werte genommen.
Quartile: Quartile teilen einen nach der Größe sortierten Datensatz in vier gleichgroße Viertel ein (ähnlich wie beim Median, der es in zwei Hälften unterteilt). Bei Quartilen interessieren uns vor allem das erste Quartil und das dritte Quartil. Das zweite Quartil haben wir bereits kennen gelernt, denn es ist der Median. Zur Bestimmung vom ersten und dritten Quartil werden die durch des Median entstandenen Hälften noch einmal auf die selbe Weise unterteilt, wie wir es bereits beim Median gemacht haben:
- Ist die Anzahl der Zahlenwerte ungerade, dann wird die mittlere Zahl ausgewählt.
- Ist die Anzahl der Zahlenwerte gerade, dann wird der Durchschnitt der beiden mittleren Werte genommen
Das erste Quartil wird häufig auch als unteres Quartil bezeichnet. Es besagt, dass 25% der Stichprobenwerte kleiner oder gleich dem ersten Quartil sind, während dementsprechend 75% der Werte größer oder gleich dem ersten Quartil sind. Das dritte Quartil wird auch als oberes Quartil bezeichnet. Analog gilt, dass 75% der Werte maximal so groß sind, wie das dritte Quartil und 25% der Werte mindestens so groß ist wie das dritte Quartil.
Der Quartilsabstand ist der Abstand bzw. die Differenz zwischen dem ersten und dem dritten Quartil.
Mit einem Boxplot ist es nun möglich, diese Größen anschaulich darzustellen:
Puh, das war viel auf einmal und sehr theoretisch. Ein Beispiel macht es anschaulicher.
Beispiel: GHR11B
Schauen wir uns doch einmal den Notenspiegel der GHR11B an.
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl | 0 | 7 | 6 | 10 | 1 | 0 |
Anstatt des Notenspiegels betrachten wir nun die Notenliste. Zudem nummerieren wir die Zahlenwerte durch.
Das Minimum und das Maximum können wir schnell ablesen
| Nr. | ||||||||||||||||||||||||
| Note | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Minimum: 2 Maximum: 5
Somit beträgt die Spannweite 3, denn die Differenz zwischen den Maximum (=5) und dem Minimum (=2) ist 3.
Da die Noten von 24 SchülerInnen angegeben sind, haben die eine gerade Anzahl an Zahlenwerten. Um den Median zu bestimmen, nehmen also den Durchschnitt vom 12. und 13. Zahlenwert.
| Nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Note | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Da es sich bei beiden Zahlenwerten um die Zahl 3 handelt, lautet der Median 3.
Durch den Median erhalten wir nun zwei Hälften:
| Nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Note | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Um das erste und das dritte Quartil zu bestimmen teilen wir diese Hälften genauso, wie bei der Bestimmung des Medians. Jede Hälfte besteht aus 12 Zahlenwerten. Somit ist das erste Quartil der Durchschnitt vom 6. und 7. Zahlenwert und das 3. Quartil der Durchschnitt vom 18. und 19. Zahlenwert.
| Nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Note | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Das erste Quartil liegt bei 2. Das dritte Quartil liegt bei 4. Der Quartilsabstand liegt also bei 2.
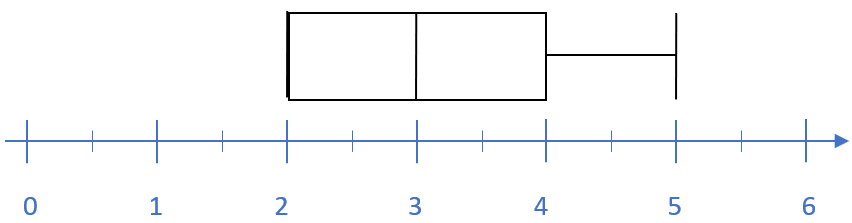
Nun haben wir alle notwendigen Größen bestimmt und sind in der Lage, den zugehörigen Boxplot darzustellen.
Dies ist nun ein besonderer Boxplot, da sowohl das Minimum als auch das erste Quartil bei 2 liegen. Wie können wir den Boxplot nun deuten?
Deutung eines Boxplots
Dem Boxplot können wir entnehmen, dass alle Noten zwischen 2 und 5 liegen. Da der Median bei 3 liegt, hat die eine Hälfte der Klasse eine 3 oder eine bessere Note geschrieben, während die andere Hälfte der Klasse eine 3 oder eine schlechtete Note geschrieben hat. Dem ersten Quartil können wir entnehmen, dass ein Viertel der Klasse Wir haben an einem Beispiel gesehen, wie ein Boxplot erstellt wird. Die Aufgabe lautet nun einen Boxplot für die Biologiearbeit der Klasse GHR11A zu erstellen.
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl | 5 | 5 | 4 | 3 | 4 | 3 |
Geben Sie die folgenden Größen an:
- Minimum: 1()
- Maximum: 6()
- Spannweite: 5()
- Median: 3()
- Erstes Quartil: 1,5()
- Drittes Quartil: 5()
- Quartilsabstand: 3,5()
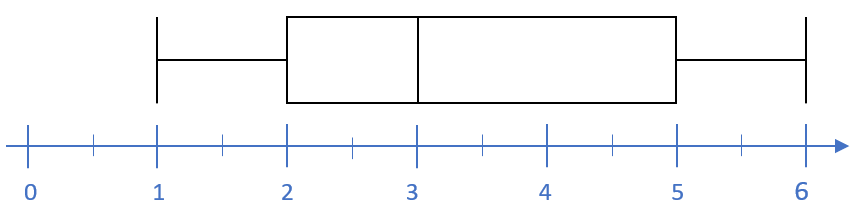
Zeichnen Sie den Boxplot auf ein Blatt Papier. Wenn Sie das erledigt haben, können Sie Ihren Boxplot hier mit der Lösung abgleichen.
Nun, wo wir beide Boxplots erstellt haben, möchten wir der Biologielehrerin der Klassen helfen zu beurteilen (dikutieren), welche der beiden Klassen besser ist.
Lehrerinh hat geasgt das die LEISTUHNGEN DER BEIDEN JKASSEN GLEICH SIND, diskutieren sie diese Aussage mithilfe des Boxplots (... Resi)