Buss-Haskert/Quadratische Gleichungen: Unterschied zwischen den Versionen
K (Erste Inhalte ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
K (Formatierungen) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 9: | Zeile 9: | ||
Bremsweg in m: s<sub>B</sub> = (<math>\tfrac{v}{10}</math>)² | Bremsweg in m: s<sub>B</sub> = (<math>\tfrac{v}{10}</math>)² | ||
{{Lösung versteckt| "s" bedeutet Weg bzw. Strecke; v steht für Geschwindigkeit (engl. velocity)|Was bedeuten s und v?|Verbergen}} | {{Lösung versteckt| "s" bedeutet Weg bzw. Strecke; v steht für Geschwindigkeit (engl. velocity)|Was bedeuten s und v?|Verbergen}} | ||
Hier handelt es sich um eine quadratische Gleichung, da die Variable v quadriert wird (v²). <br> | Hier handelt es sich um eine quadratische Gleichung, da die Variable v quadriert wird (v²). | ||
Berechne den Bremsweg, wenn das Auto mit einer Geschwindigkeit von 30km/h fährt, also v=30 und wenn es mit einer Geschwindigkeit von 50km/h unterwegs ist. Was fällt dir auf?<br> | |||
<br> | |||
Berechne den Bremsweg, wenn das Auto mit einer Geschwindigkeit von 30km/h fährt, also v=30 und wenn es mit einer Geschwindigkeit von 50km/h unterwegs ist. | |||
Was fällt dir auf?<br> | |||
Vor Schulen oder Kindergärten sollten die Bremswege möglichst kurz sein. Wie schnell darf ein Auto fahren, damit der Bremsweg höchstens 4m beträgt? | Vor Schulen oder Kindergärten sollten die Bremswege möglichst kurz sein. Wie schnell darf ein Auto fahren, damit der Bremsweg höchstens 4m beträgt? | ||
{{Lösung versteckt|Wenn v=30 beträgt, ist s<sub>B</sub> = (<math>\tfrac{30}{10}</math>)² = 3² = 9 (m)<br> | {{Lösung versteckt|Wenn v=30 beträgt, ist s<sub>B</sub> = (<math>\tfrac{30}{10}</math>)² = 3² = 9 (m)<br> | ||
| Zeile 35: | Zeile 39: | ||
Sie haben immer die Form ax² = d (hier umgeformt <math>\tfrac{1}{100}</math>v² = s<sub>B</sub>) | Sie haben immer die Form ax² = d (hier umgeformt <math>\tfrac{1}{100}</math>v² = s<sub>B</sub>) | ||
{{Box|Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:<br> | {{Box|1=Rein quadratische Gleichungen|2=Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:<br> | ||
ax² = d|Arbeitsmethode}} | ax² = d|3=Arbeitsmethode}} | ||
Diese Gleichungen zu lösen hast du schon in der 9. Klasse gelernt. Wiederhole dein Wissen mithilfe der nachfolgenden Aufgaben.Sicher hast du schon eine Idee. Löse die folgenden Beispiele: | Diese Gleichungen zu lösen hast du schon in der 9. Klasse gelernt. Wiederhole dein Wissen mithilfe der nachfolgenden Aufgaben.Sicher hast du schon eine Idee. Löse die folgenden Beispiele: | ||
| Zeile 45: | Zeile 49: | ||
Beispiel: | Beispiel: | ||
1. x² = 169 kannst du auch schreiben als x² - 169 = 0. Du berechnest also die Nullstellen der Funktion f(x) = x² - 169 | 1. x² = 169 kannst du auch schreiben als x² - 169 = 0. Du berechnest also die Nullstellen der Funktion f(x) = x² - 169 | ||
Version vom 20. Oktober 2020, 18:13 Uhr
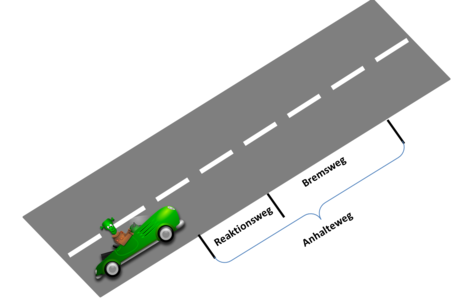
In der Fahrschule lernst du eine Faustformel für die Berechnung des Bremsweges:
Bremsweg in m: sB = ()²
Hier handelt es sich um eine quadratische Gleichung, da die Variable v quadriert wird (v²).
Berechne den Bremsweg, wenn das Auto mit einer Geschwindigkeit von 30km/h fährt, also v=30 und wenn es mit einer Geschwindigkeit von 50km/h unterwegs ist.
Was fällt dir auf?
Vor Schulen oder Kindergärten sollten die Bremswege möglichst kurz sein. Wie schnell darf ein Auto fahren, damit der Bremsweg höchstens 4m beträgt?
Du siehst: Mathe ist überall! Du erarbeitest nun die Grundlagen zum Lösen solcher quadratischer Gleichungen.
1) Was sind quadratische Gleichungen?
Quadratische Gleichungen sind Gleichungen, in denen die Variable in zweiter Potenz (also z.B. x²) vorkommt.
Erinnerung: Lineare Gleichungen sind Gleichungen, in denen die Variable nur in erster Potenz (also z.B. x = x1) vorkommt.
Entscheide in der nachfolgenden LearningApp, ob es sich um eine quadratische Gleichung handelt oder nicht.
2) Wie löse ich quadratische Gleichungen?
Quadratische Gleichungen kannst du zeichnerisch und rechnerisch lösen. Nutze für die zeichnerische Lösung GeoGebra und prüfe so immer deine rechnerischen Lösungen. Es gibt verschiedene Formen quadratischer Gleichungen. Die Lösungsstrategie hängt von der Form ab. Dies erklären die folgenden Kapitel.
2.1) Rein quadratische Gleichungen lösen
In der obigen Faustformel kommt die Variable v nur in quadratischer Form vor, also nur als v². Solche Gleichungen heißen "rein quadratisch". Sie haben immer die Form ax² = d (hier umgeformt v² = sB)
Diese Gleichungen zu lösen hast du schon in der 9. Klasse gelernt. Wiederhole dein Wissen mithilfe der nachfolgenden Aufgaben.Sicher hast du schon eine Idee. Löse die folgenden Beispiele: 1. x² = 169 2. 2x² + 10 = 10
Du kannst diese Gleichungen auch grafisch lösen:
Beispiel:
1. x² = 169 kannst du auch schreiben als x² - 169 = 0. Du berechnest also die Nullstellen der Funktion f(x) = x² - 169
