Buss-Haskert/Ähnlichkeit und Strahlensätze: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
K (Geogebra Applet ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| (85 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+Wo stehst du? Teste dein Vorwissen! | ||
!Du kannst | !Du kannst | ||
!Übungen im Buch | !Übungen im Buch | ||
| Zeile 30: | Zeile 30: | ||
| -Gleichungen und Formeln umstellen | | -Gleichungen und Formeln umstellen | ||
|S. 90 Nr. 6,7 | |S. 90 Nr. 6,7 | ||
| | |{{LearningApp|app=pnf1nu66t20|width=100%|height=100px}}{{LearningApp|app=p1jsmdvrc20|width=100%|height=100px}} | ||
|- | |- | ||
| -Dreiecke konstruieren | | -Dreiecke konstruieren | ||
| Zeile 81: | Zeile 81: | ||
===1) Vergrößern und Verkleinern=== | |||
Ein Zeichengerät zum Vergrößern bzw. Verkleinern von Figuren ist der Pantograph. Er wurde früher zum Verkleinern oder Vergrößern von Plänen oder Karten genutzt. Im nachfolgenden Applet kannst du dieses Gerät ausprobieren. | |||
Klicke in das Feld 1 und wähle "Spur ein". Dann ziehe am blauen Punkt. Was passiert? | |||
Kannst du mit dem Feld 2 herausfinden, mit welchem Faktor vergrößert wird? | |||
<ggb_applet id="QFQGTZVE" width="1000" height="610"></ggb_applet> | |||
Das folgende Geogebra-Applet zeigt den Buchstaben T. Verändere die Größe des rechten Buchstaben mithilfe des Schiebereglers. | |||
<ggb_applet id="xfawm8bn" width="1000" height="610" /> | |||
Welche Bedeutung hat der Schieberegler? | |||
<br /> | |||
{{Box|Vergrößern und Verkleinern|Ziehe die richtigen Lösungen in die Lücken und schreibe dann den Merksatz in dein Heft ab.|Arbeitsmethode}} | |||
<div class="lueckentext-quiz"> | |||
Beim Vergrößern oder Verkleinern einer Figur werden alle Streckenlängen mit demselben '''Faktor k''' multipliziert. Dabei ist k immer eine '''positive''' Zahl. | |||
Für '''k > 1''' wird die Figur vergrößert. | |||
Für '''k < 1''' wird die Figur verkleinert. | |||
Für die Streckenlängen gilt a' = k∙a, also gilt k = '''<math>{\operatorname{a'}\over\operatorname{a}\!}</math>'''.</div> | |||
{{Box|Übung 1: Vergrößern und Verkleinern|Zeichne die Buchstaben H oder L in dein Heft, vergrößere und verkleinere das Original und gib den Faktor k an.|Üben}} | |||
{{Lösung versteckt|Schau ins Buch S. 92 oben, dort findest du Beispiele für den Buchstaben L.|Tipp|Verbergen}} | |||
{{Box| Übung 2: Rechtecke vergrößern und verkleinern|Lies im Buch S. 92 unten Beispiel a). Bearbeite danach S. 93 Nr. 1, 2, 3 und 4.|Üben}} | |||
{{Lösung versteckt|Link GeoGebra-Applet https://www.geogebra.org/classic/rhctngwz|GeoGebra-Applet zu Nr. 1|Verbergen}} | |||
{{Lösung versteckt|1=Seitenlänge des Originals: a=7cm | |||
Seitenlänge des vergrößerten Bildes: a=10,5cm | |||
Erinnerung: k = <math>{\operatorname{a'}\over\operatorname{a}\!}</math>=..., denn a'=k∙a | |||
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=... | |||
<ggb_applet id="bznvvgsb" width="1000" height="610"></ggb_applet>|2=Tipp zu Nr. 2|3=Verbergen}} | |||
{{Lösung versteckt|1=Erinnerung: k = <math>{\operatorname{a'}\over\operatorname{a}\!}</math>=<math>{\operatorname{10}\over\operatorname{6}\!}</math>=... (Kürze!) | |||
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=...Setze k ein und berechne.|2=Tipp zu Nr. 3|3=Verbergen}} | |||
{{Box|Übung 3: Vielecke vergrößern|Lies im Buch S. 93 oben Beispiel b). Bearbeite danach S. 94 Nr. 6 und 7|Üben}} | |||
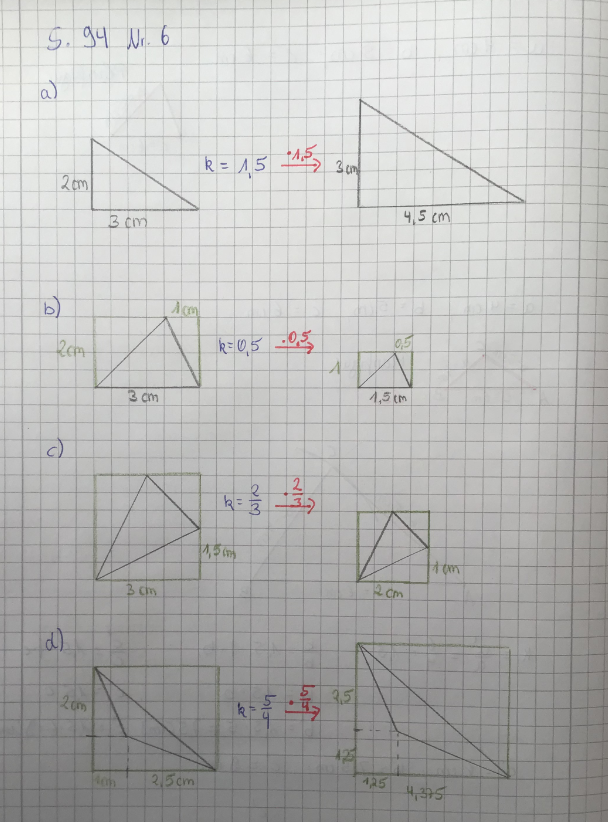
{{Lösung versteckt|[[Datei:S.94 Nr. 6.png]]|Lösung zu Nr. 6|Verbergen}} | |||
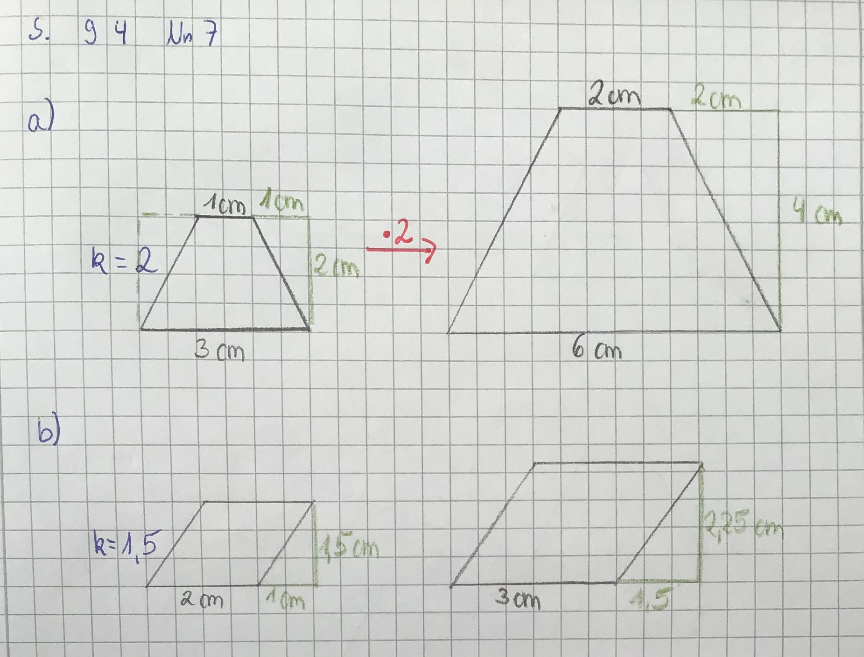
{{Lösung versteckt|[[Datei:S. 94 Nr. 7 Lösung.png]]|Lösung zu Nr.7|Verbergen}} | |||
{{Box|Übung 4: Wie ändert sich der Flächeninhalt beim Vergrößern und Verkleinern?|Bearbeite S. 94 Nr. 11. Das nachfolgende GeoGebra-Applet hilft dabei. | |||
a) Vergrößere das Rechteck mit dem Faktor k (Schieberegler). Wie ändert sich der Flächeninhalt? Notiere in einer Tabelle, wie auf S.94 Nr. 11a) dargestellt. (Lies die Tabelle spaltenweise.)|Üben}} | |||
<ggb_applet id="usyfabzs" width="1000" height="610" /> | |||
{{Lösung versteckt|1=Beim Vergrößer bzw. verkleinern eines Rechtecks ändert sich der Flächeninhalt mit dem Quadrat des Vergrößerunsfaktors k. Also A' = k²· A. | |||
A = a · b , vergrößere/verkleinere das Rechteck mit dem Faktor k, also a'=k·a und b'=k·b, dann gilt | |||
A’ = a’ · b’ = k·a · k·b = k² · a · b = k² · A|2=Tipp zu S. 94 Nr. 11c|3=Verbergen}} | |||
{{Box|Übung 5: Der Kopierer| Wende dein Wissen aus Übung 4 an und löse S. 95 Nr. 18.|Üben}} | |||
Nutze auch hier das GeoGebra-Applet. Stelle k=71%=0,71 und danach k=141%=1,41 ein. Wie ändert sich der Flächeninhalt? | |||
<ggb_applet id="bwbxqydh" width="1000" height="610" /> | |||
{{Lösung versteckt| | |||
{{Lösung versteckt|1=Wenn k =71% ist, dann wird die Fläche halbiert: f = 0,5. | |||
Wenn k=141% ist, dann wird die Fläche verdoppelt: f = 2. | |||
Erklärung: | |||
A'=k²∙A=0,71²∙A <math>\approx</math>0,5∙A, denn 0,71²=0,5041<math>\approx</math>0,5. | |||
A'=k²∙A=1,41²∙A <math>\approx</math>2∙A, denn 1,41²=1,9881<math>\approx</math>2.|2=Tipp zu a)|3=Verbergen}} | |||
{{Lösung versteckt|1=Tipp zu b): Bestimme zunächst den Vergrößerungsfaktor k für die Seitenlängen mit k=<math>\frac{a'}{a}</math>=a':a | |||
29,7 : 25,8 = 1,15 = 115 %, 21 : 19 = 1,10 = 110 %. | |||
Damit alles auf der Seite abgebildet wird, sollte der Kopierer also auf 110 % gestellt werden.|2=Tipp zu b)|3=Verbergen}}|Tipps und Lösungen zu S.95 Nr.18|Verbergen}} | |||
{{Box|Übung 6: Wie verändert sich das Volumen beim Vergrößern und Verkleinern?|Bearbeite S.94 Nr.12. Das nachfolgende GeoGebra-Applet hilft dir dabei.|Üben}} | |||
Das GeoGebra-Applet zeigt einen Quader mit a=3cm; b=2cm und c=1cm. Vergrößere die Seitenlängen mit dem Faktor k (Schieberegler). Wie verändert sich das Volumen des Quaders? | |||
Notiere V<sub>1</sub>=6cm³; V<sub>2</sub> = 48cm³ = ____ ∙V<sub>1</sub>; V<sub>3</sub> = ... = ____∙V<sub>1</sub>; usw. | |||
Was fällt dir auf? | |||
<ggb_applet id="qzknx4ue" width="1000" height="610" /> | |||
{{Lösung versteckt|1=1=Vergrößert man die Kantenlängen des Quaders mit k, so vergrößert sich das Volumen des Quaders mit k³. Also V' = k³· V. | |||
V = a · b · c , vergrößere/verkleinere die Kantenlängen mit dem Faktor k, also a'=k·a und b'=k·b, c=k·c' dann gilt | |||
V’ = a’· b’· c’= k·a · k·b · k·c = k³ · a · b · c = k³ · V|2=Allgemeine Regel zu S. 94 Nr. 12a|3=Verbergen}} | |||
===2) Ähnliche Figuren=== | |||
Schreibe den Merksatz in dein Heft: | Schreibe den Merksatz in dein Heft: | ||
| Zeile 91: | Zeile 182: | ||
Dabei müssen zwei Bedingungen gelten: | Dabei müssen zwei Bedingungen gelten: | ||
- Alle Winkel sind gleich groß. | - Alle Winkel sind gleich groß. | ||
| Zeile 107: | Zeile 196: | ||
<br /> | <br /> | ||
{{Box|Aufgabe 2|Sucht in eurer Umgebung im geometrischen Sinn ähnliche Figuren, macht ein Foto und ladet es im Gruppenorder Mathematik hoch|Üben}} | {{Box|Aufgabe 2|Sucht in eurer Umgebung im geometrischen Sinn ähnliche Figuren, macht ein Foto und ladet es im Gruppenorder Mathematik hoch.|Üben}} | ||
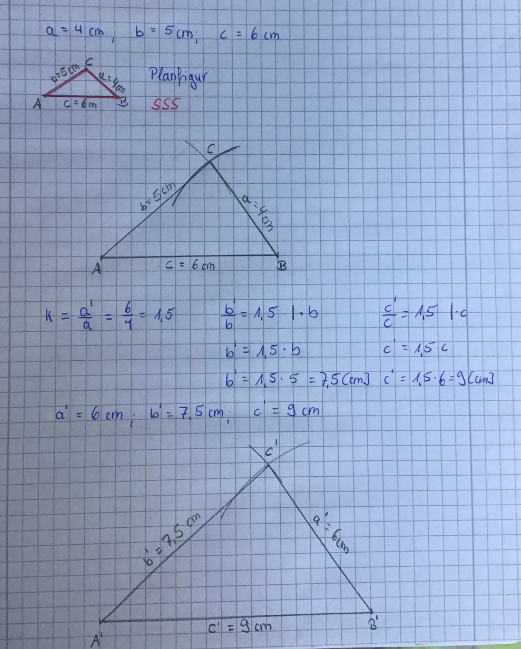
{{Box|1=Beispiel: Ähnliche Dreiecke konstruieren|2=Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. Konstruiere dann das dazu ähnliche Dreieck A'B'C' mit a'=6cm.|3=Arbeitsmethode}} | |||
1. Schritt: Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. | |||
Erinnerung: Kongruenzsatz SSS | |||
In der nachfolgenden App sind die Schritte zur Konstruktion dargestellt, du musst sie in die richtige Reihenfolge bringen. Übertrage danach die Konstruktion in dein Heft. | |||
{{LearningApp|app=p16u152nj20|width=100%|height=800px}} | |||
{{Lösung versteckt|Das verlinkte GeoGebra-Datei zeigt die die Konstruktion mit den Kongruenzsatz SSS noch einmal Schritt für Schritt: https://www.geogebra.org/m/CCQrYPXZ|Wiederholung Konstruktion mit dem Kongruenzsatz SSS|Verbergen}} | |||
2. Schritt: | |||
Berechne den Vergrößerungsfaktor k und damit dann b' und c'. | |||
{{Lösung versteckt|1=k=<math>\tfrac{a'}{a}</math>=<math>\tfrac{6}{4}</math>=1,5; also gilt | |||
<math>\tfrac{b'}{b}</math>=1,5 | |||
<math>\tfrac{b'}{5}</math>=1,5 | |||
b'=1,5·5 | |||
b'=7,5 [cm]; | |||
ebenso gilt c'=1,5·c = 1,5·6 = 9[cm]|2=Lösung anzeigen|3=Verbergen}} | |||
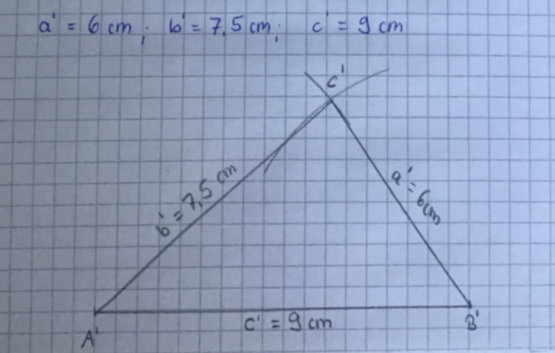
3. Schritt: | |||
Konstruiere das Dreieck A'B'C' (Konstruktion mit SSS wie oben). | |||
[[Datei:Dreieck A'B'C'.png|555x555px]] | |||
{{Lösung versteckt|[[Datei:Hefteintrag zum Beispiel.png|Hefteintrag zum Beispiel.png]]|Hilfe:So müsste dein Hefteintrag aussehen|Verbergen}} | |||
{{Box|1=Übung 3: Ähnliche Dreiecke - Berechnungen|2=Löse zunächst die folgende LearningApp und mit derselben ausführlichen Schreibweise S. 97 Nr. 2. Kontrolliere deine Ergebnisse mit dem nachfolgenden GeoGebra-Applet.|3=Üben}} | |||
{{LearningApp|app=p0oommxqn20|width=100%|height=600px}} | |||
Prüfe deine Lösungen zu S. 97 Nr. 2: Stelle k so ein, dass die jeweiligen Seitenlängen zur Aufgabe passen. Dann lies k und die fehlenden Seitenlängen ab. | |||
<ggb_applet id="atph52nb" width="800" height="610" /> | |||
{{Box|Übung 4: Konstruktion ähnlicher Dreiecke|Löse schrittweise (wie im Beispiel oben) | |||
S. 97 Nr. 1 a), d) und | |||
S. 97 Nr. 3. | |||
Prüfe deine Lösungen mit dem zugehörigen GeoGebra-Applet.|Üben}} | |||
{{Lösung versteckt|{{Lösung versteckt|1=k=<math>\tfrac{a'}{a}</math>=<math>\tfrac{8}{4}</math>=2; also gilt | |||
<math>\tfrac{b'}{b}</math>=2 | |||
<math>\tfrac{b'}{5}</math>=2 | |||
b'=2·5 | |||
b'=10 [cm]; | |||
ebenso gilt c'=2·c = 2·6 = 10[cm]|2=Tipp zu a)|3=Verbergen}} | |||
{{Lösung versteckt|1=k=<math>\tfrac{b'}{b}</math>=<math>\tfrac{6}{5}</math>=1,2; also gilt | |||
<math>\tfrac{a'}{a}</math>=1,2 | |||
<math>\tfrac{a'}{4}</math>=1,2 | |||
a'=1,2·4 | |||
a'=4,8 [cm]; | |||
ebenso gilt c'=1,2·c = 1,2·6 = 7,2[cm]|2=Tipp zu d)|3=Verbergen}}|Tipps zu S.97 Nr.1}} | |||
Prüfe deine Lösung von S. 97 Nr. 1 a,d: | |||
<ggb_applet id="wshyybyn" width="800" height="610"></ggb_applet>Prüfe deine Lösung von S. 97 Nr. 3 | |||
<ggb_applet id="czznt9y4" width="800" height="610"></ggb_applet> | |||
{{Box|Übung 5: Vermischte Übungen|Löse S. 97 Nr. 4, 5, 6, 7 und 8 im Heft.|Üben}} | |||
{{Lösung versteckt|1=Berechne jeweils das Verhältnis der Bildstreckenlängen zu den Originallängen. Es muss immer gleich sein, wenn die Dreiecke ähnlich sind (nämlich k). Gilt <math>\tfrac{a'}{a}</math>=<math>\tfrac{b'}{b}</math>=<math>\tfrac{c'}{c}</math>|2=Tipp zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|1=Bestimme zunächst den Ähnlichkeitsfaktor k=<math>\tfrac{a'}{a}</math>, denn nur von diesen beiden Seiten kennst du die Bild- und Originalstreckenlänge. Dann kannst du die fehlenden Längen von b' und c durch Umstellen der Formel k=<math>\tfrac{b'}{b}</math> nach b' und k=<math>\tfrac{c'}{c}</math> nach c berechnen. {{Lösung versteckt|1=Umstellen der Formel nach b' | |||
k=<math>\tfrac{b'}{b}</math> I∙b | |||
also gilt k∙b = b' (einsetzen und ausrechen)|2=Umstellen der Formel nach b|3=Verbergen}}{{Lösung versteckt|1=Umstellen der Formel c | |||
k=<math>\tfrac{c'}{c}</math> I∙c | |||
k∙c = c' I:k | |||
c = <math>\tfrac{c'}{k}</math> (einsetzen und ausrechnen)|2=Umstellen der Formel nach c|3=Verbergen}} | |||
|2=Tipp zu Nr. 5|3=Verbergen}} | |||
===1) | {{Lösung versteckt|1=zu a) Es gilt k=<math>\tfrac{2}{3}</math>. | ||
zu b) Die Dreiecke sind ähnlich, also stimmen in drei Winkeln überein. Sie stimmen in zwei Seiten überein, allerdings ist die Reihenfolge der Seiten unterschiedlich (a = b’; b = c’).|2=Tipp zu Nr. 6}} | |||
{{Lösung versteckt|1=Bestimme zunächst den Ähnlichkeitsfaktor k mit u und u'. Da der Umfang die Summe der Seitenlängen ist, gilt für den Ähnlichkeitsfaktor k = <math>\tfrac{u'}{u}</math>. Bestimme k (Zwischenergebnis: k=1,5). Damit kannst du nun die Längen des Dreiecks A'B'C' bestimmen. | |||
Du kannst deine Rechnunge wieder mit GeoGebra prüfen:https://www.geogebra.org/classic/qbwddt9z|2=Tipp zu Nr. 7|3=Verbergen}} | |||
{{Lösung versteckt| | |||
{{Lösung versteckt|Erinnerst du dich an den Faktor, mit dem sich der Flächeninhalt bei der Vergrößerung der Seitenlängen mit der Zahl k? (Vgl. Übung 4 im Kapitel 1), scrolel noch einmal hoch.|Tipp 1 zu Nr. 8|Verbergen}} | |||
{{Lösung versteckt|1=Wenn die Seitenlängen mit dem Faktor k vergrößert werden, vergrößert sich der Flächeninhalt mit dem Faktor k². Also gilt | |||
k²=4 I<math>\surd</math> | |||
k = 2 | |||
Die Seitenlängen werden also jeweils verdoppelt.|2=Tipp 2 zu Nr. 8|3=Verbergen}} | |||
{{Lösung versteckt|Mit GeoGebra kannst du deine Lösung überprüfen: https://www.geogebra.org/classic/gpghwvrm|Lösungskontrolle zu Nr. 8 (GeoGebra)|Verbergen}}|Tipps zu Nr. 8|Verbergen}} | |||
===3) Strahlensätze=== | |||
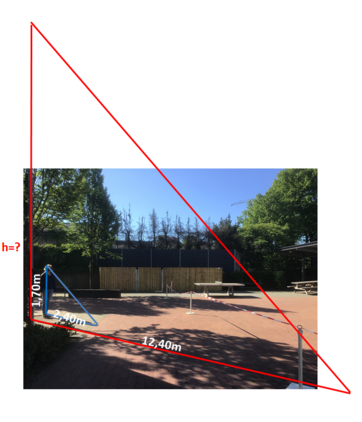
In der Umwelt lassen viele Strecken sich nicht messen, wie z.B. die Höhe von Bäumen oder die Breite eines Sees. Hier hilft die Mathematik! | |||
<div class="grid"> | |||
<div class="width-1-2">[[Datei:Einsteigsbeispiel Baumhöhe Schule.png|422x422px]]</div> | |||
<div class="width-1-2">[[Datei:Einsteigsbeispiel Breite See.png]]</div> | |||
</div> | |||
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen): | |||
{{Box|Aufgabensammlung Schattenmethode|Suche bei Sonnenschein ein Gebäude, einen Baum, eine Straßenlaterne, ein Windrad,... mit zugehörigem Schattenwurf und fotografiere den Gegenstand samt Schatten. Nun wird gemessen: Miss die Länge des Schattens des Gegenstandes und miss deine Körpergröße sowie die Länge deines eigenen Schattens. Das Foto samt der 3 gemessenen Längen lade im Gruppenordner Mathematik deiner Klasse hoch. Wir werden damit später berechnen, wie hoch das Gebäude, der Baum, die Laterne, das Windrad... ist. Die Aufgabe oben (Baumhöhe) und das Bild S. 103 Nr. 10 zeigen mögliche Situationen.|Lösung|Icon=hdg-smartphone03}} | |||
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst. | |||
{{Box|1=Einstiegsbeispiel|2=Konstruiere die ähnlichen Dreiecke: ① a = 3cm; c = 5cm; β = 110° und ② a = 6cm; c = 10 cm; β = 110°. | |||
a) Begründe, warum die Dreiecke ähnlich sind. | |||
b) Bestimme den Streckungsfaktor k. Notiere verschiedene Möglichkeiten. | |||
c) Bilde verschiedene Streckenverhältnisse <math>\tfrac{a}{b}</math>, <math>\tfrac{a'}{b'}</math>, <math>\tfrac{a'}{a}</math> uws. | |||
Was fällt dir auf?|3=Üben}} | |||
[[Datei:Dreiecke Konstruktion Einstieg Strahlensätze 2.png]] | |||
{{Lösung versteckt|1= Für die Streckenverhältnisse ergeben sich immer gleiche Werte: | |||
<math>\tfrac{a}{b}</math>=<math>\tfrac{3}{6,7}</math> <math>\approx</math>0,45 | |||
<math>\tfrac{a'}{b'}</math>=<math>\tfrac{6}{13,4}</math> <math>\approx</math>0,45 | |||
<math>\tfrac{a}{c}</math>=<math>\tfrac{3}{5}</math> = 0,6 | |||
< | <math>\tfrac{a'}{c'}</math>=<math>\tfrac{6}{10}</math> = 0,6 | ||
<math>\tfrac{b}{c}</math>=<math>\tfrac{6,7}{5}</math> <math>\approx</math> 1,3 | |||
< | <math>\tfrac{b'}{c'}</math>=<math>\tfrac{13,4}{10}</math> <math>\approx</math> 1,3 | ||
<math>\tfrac{a'}{a}</math>=<math>\tfrac{6}{3}= 2</math> Erinnerung: Das ist der Streckungsfaktor k | |||
<math>\tfrac{b'}{b}</math>=<math>\tfrac{13,4}{6,7}</math> = 2 | |||
<math>\tfrac{c'}{c}</math>=<math>\tfrac{10}{5}</math> = 2|2=Streckenverhältnisse|3=Verbergen}} | |||
<div class="grid"> | |||
<div class="width-1-2">Diese Dreiecke "schieben" wir nun übereinander. | |||
[[Datei:Dreiecke Konstruktion übereinander gelegt mit Maßen.png|602x602px]].</div> | |||
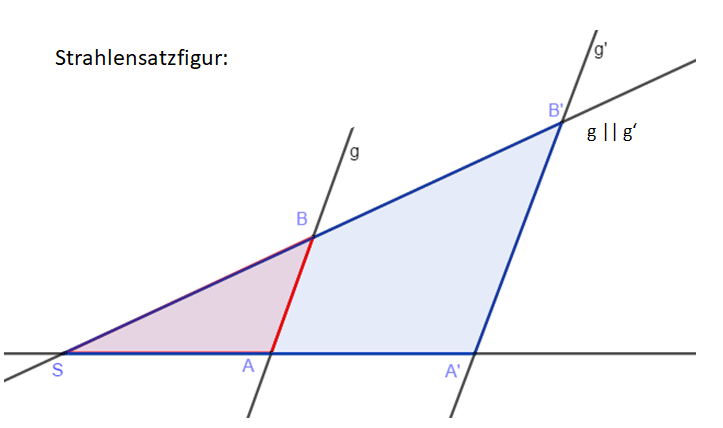
<div class="width-1-2">Und wenn wir die Seiten jeweils mit Geraden ergänzen und die Beschriftungen anpassen, erhalten wir eine sogenannte <b>Strahlensatzfigur</b>. Sie besteht aus zwei Geraden, die von zwei Parallelen geschnitten werden. Es entstehen dabei unsere zwei kongruenten Dreiecke. | |||
[[Datei:Strahlensatzfigur zu Beispieldreiecken.png]]</div> | |||
</div> | </div> | ||
Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c =<math>\overline{SA}</math> ; c' = <math>\overline{SA'}</math> usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die <b>Strahlensätze</b>. | |||
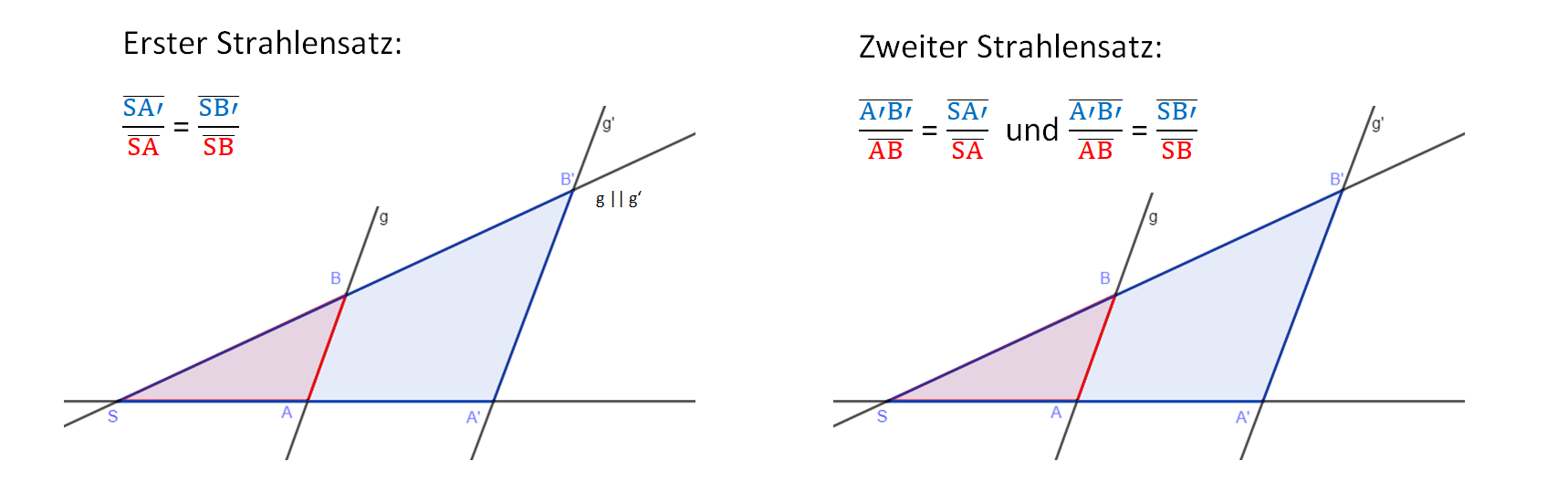
{{Box|1=Hefteintrag: Die Strahlensätze |2=Werden zwei sich schneidende Geraden von zwei parallelen Geraden geschnitten, entstehen zwei zueinander ähnliche Dreiecke SAB und SA'B'. | |||
Die Seitenlängen einander entsprechender Seiten stehen im gleichen Verhältnis zueinander. | |||
[[Datei:Strahlensätze.png]] | |||
Schreibe die Strahlensätze in dein Heft und zeichne auch die Strahlensatzfiguren|3=Arbeitsmethode}} | |||
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen. | |||
{{Lösung versteckt|1=Die Streckenverhältnisse des ersten Strahlensatz heißen für unsere ähnlichen Dreiecke im Beispiel | |||
{{ | <math>\tfrac{c'}{c}</math>=<math>\tfrac{b'}{b}</math>=k | ||
{{ | Die Streckenverhältnisse des zweiten Strahlensatzes sind in unserem Beispiel entsprechend | ||
<math>\tfrac{a'}{a}</math>=<math>\tfrac{c'}{c}</math>=k und <math>\tfrac{a'}{a}</math>=<math>\tfrac{b'}{b}</math>=k | |||
|2=Erklärung am Einsteigsbeispiel|3=Verbergen}} | |||
Zum besseren Verständnis noch einmal links die Erklärung und rechts einige Beispiele in Videos: | |||
<div class="grid"> | |||
<div class="width-1-2">{{#ev:youtube|xcsKEsB0cqE|460|center}}</div> | |||
<div class="width-1-2">{{#ev:youtube|ow1RXss_T4M|460|center}}</div> | |||
</div> | |||
<div class="grid"> | |||
<div class="width-1-2">{{#ev:youtube|iG8D5LpH2iw|460|center}}</div> | |||
<div class="width-1-2">{{#ev:youtube|XmFLkHBJFy8|460|center}}</div> | |||
</div><br />{{Box|Übung 1|Formuliere die Strahlensätze in der folgenden App.|Üben}} | |||
{{LearningApp|app=pd9ma7p5j20|width=100%|heigth=800px}} | |||
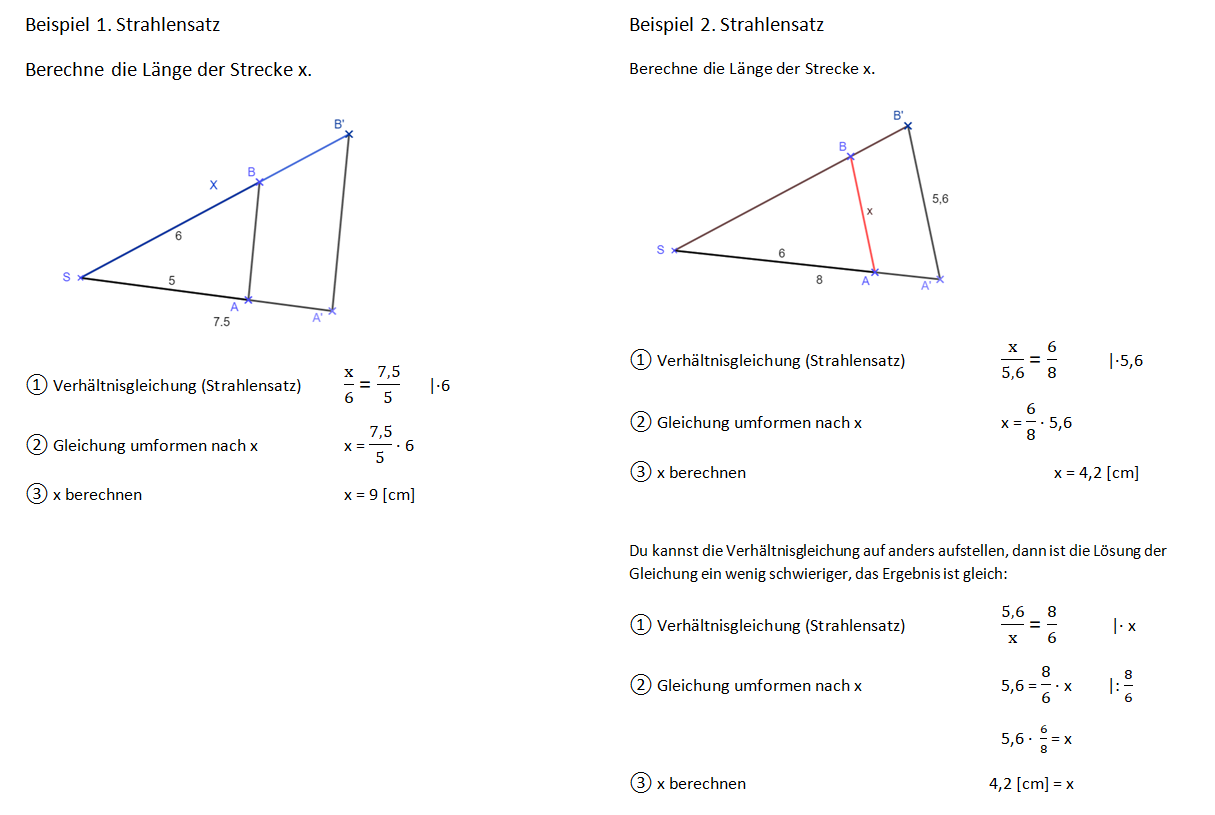
{{Box|Längen mit den Strahlensätzen berechnen: Beispiele|Um Längen mit den Strahlensätzen zu berechnen, gehen wir schrittweise vor. Übertrage die Beispiele in dein Heft.|Arbeitsmethode}} | |||
[[Datei:Beispiele 1 und 2 Längen mit dem Strahlensatz berechnen.png]] | |||
{{Box|Übung 2|Bearbeite Buch S. 99 Nr. 1 und 2, | |||
S. 100 Nr. 3 und | |||
S. 100 Nr. 7 a, b, d. | |||
Notiere die Lösungsschritte ausführlich wie in den Beispielen. | |||
|Üben}} | |||
Du kannst eine Ergebnisse mithilfe des GeoGebra-Applets prüfen. Stelle dazu die Längen mit den Schiebereglern passend ein. | |||
Um die Strecke <math>\overline{SB'}</math> einzustellen, nutze den Schieberegler für die Strecke <math>\overline{SB}</math> (oder bei Nr. 3 auch Schieberegler für die Strecke <math>\overline{SA}</math>) und verändere diese Länge so lange, bis der passende Wert für die Länge von <math>\overline{SB'}</math> erscheint. | |||
Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse. | |||
<ggb_applet id="ktgvdhq4" width="800" height="610"></ggb_applet> | |||
{{ | {{Box|Die Strahlensätze für die x-Figur|Bisher haben wir nur Strahlensatzfiguren betrachtet, bei denen beide ähnlichen Dreiecke auf einer Seite vom Punkt S lagen. Bewege die roten Punkte beim folgenden GeoGebra-Applet und erkläre, wie sich die Strahlensatzfigur ändert. Welche Strecken entsprechen sich nun?|Arbeitsmethode}} | ||
<ggb_applet id="CQafknDF" width="800" height="610"></ggb_applet> | |||
{{Box|Übung 3|Löse Buch S. 100 Nr. 4 und 7c. Kontrolliere deine Ergebnisse mit GeoGebra.|Üben}} | |||
Aktuelle Version vom 7. Mai 2020, 16:58 Uhr
SEITE IM AUFBAU!!
Vorwissen zum Thema Ähnlichkeit
| Du kannst | Übungen im Buch | Übungen online |
|---|---|---|
| -Zahlen runden | S. 90 Nr. 1 |
|
| -Brüche ohne Taschenrechner multiplizieren | S. 90 Nr. 2 |
|
| -Winkel berechnen | S.90 Nr. 3 |
|
| -Größen umwandeln | S. 90 Nr. 4 |
|
| -Umfang und Flächeninhalt von Figuren berechnen | S.90 Nr. 5 |
|
| -Gleichungen und Formeln umstellen | S. 90 Nr. 6,7 |
|
| -Dreiecke konstruieren | S. 90 Nr. 8 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
Ähnlichkeit - Beispiel aus dem Alltag
Das nachfolgende GeoGebra-Applet zeigt zwei Dreiecke, die im geometrischen Sinn ähnlich sind. Bewege die Punkte B und C und beobachte die Größe der Innenwinkel.

Kreuze die richtige Aussage an. (!Wenn man den Punkt C verschiebt, ändern sich nur beim rechten Dreieck die Winkel.) (!Ähnliche Dreiecke haben immer parallele Seiten) (Die Winkel in beiden Dreiecken sind immer gleich groß.) (!Genau ein Winkel in beiden Dreiecken ist gleich groß.)
Und nun untersuche die Seitenlängen der Dreiecke:

1) Vergrößern und Verkleinern
Ein Zeichengerät zum Vergrößern bzw. Verkleinern von Figuren ist der Pantograph. Er wurde früher zum Verkleinern oder Vergrößern von Plänen oder Karten genutzt. Im nachfolgenden Applet kannst du dieses Gerät ausprobieren.
Klicke in das Feld 1 und wähle "Spur ein". Dann ziehe am blauen Punkt. Was passiert?
Kannst du mit dem Feld 2 herausfinden, mit welchem Faktor vergrößert wird?

Das folgende Geogebra-Applet zeigt den Buchstaben T. Verändere die Größe des rechten Buchstaben mithilfe des Schiebereglers.

Welche Bedeutung hat der Schieberegler?
Beim Vergrößern oder Verkleinern einer Figur werden alle Streckenlängen mit demselben Faktor k multipliziert. Dabei ist k immer eine positive Zahl.
Für k > 1 wird die Figur vergrößert.
Für k < 1 wird die Figur verkleinert.
Für die Streckenlängen gilt a' = k∙a, also gilt k = .
Seitenlänge des Originals: a=7cm Seitenlänge des vergrößerten Bildes: a=10,5cm Erinnerung: k = =..., denn a'=k∙a
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=...

Erinnerung: k = ==... (Kürze!)
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=...Setze k ein und berechne.

Beim Vergrößer bzw. verkleinern eines Rechtecks ändert sich der Flächeninhalt mit dem Quadrat des Vergrößerunsfaktors k. Also A' = k²· A.
A = a · b , vergrößere/verkleinere das Rechteck mit dem Faktor k, also a'=k·a und b'=k·b, dann gilt
A’ = a’ · b’ = k·a · k·b = k² · a · b = k² · A
Nutze auch hier das GeoGebra-Applet. Stelle k=71%=0,71 und danach k=141%=1,41 ein. Wie ändert sich der Flächeninhalt?

Wenn k =71% ist, dann wird die Fläche halbiert: f = 0,5.
Wenn k=141% ist, dann wird die Fläche verdoppelt: f = 2.
Erklärung:
A'=k²∙A=0,71²∙A 0,5∙A, denn 0,71²=0,50410,5.
A'=k²∙A=1,41²∙A 2∙A, denn 1,41²=1,98812.Tipp zu b): Bestimme zunächst den Vergrößerungsfaktor k für die Seitenlängen mit k==a':a
29,7 : 25,8 = 1,15 = 115 %, 21 : 19 = 1,10 = 110 %.
Damit alles auf der Seite abgebildet wird, sollte der Kopierer also auf 110 % gestellt werden.
Das GeoGebra-Applet zeigt einen Quader mit a=3cm; b=2cm und c=1cm. Vergrößere die Seitenlängen mit dem Faktor k (Schieberegler). Wie verändert sich das Volumen des Quaders? Notiere V1=6cm³; V2 = 48cm³ = ____ ∙V1; V3 = ... = ____∙V1; usw. Was fällt dir auf?

1=Vergrößert man die Kantenlängen des Quaders mit k, so vergrößert sich das Volumen des Quaders mit k³. Also V' = k³· V.
V = a · b · c , vergrößere/verkleinere die Kantenlängen mit dem Faktor k, also a'=k·a und b'=k·b, c=k·c' dann gilt
V’ = a’· b’· c’= k·a · k·b · k·c = k³ · a · b · c = k³ · V
2) Ähnliche Figuren
Schreibe den Merksatz in dein Heft:

1. Schritt: Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. Erinnerung: Kongruenzsatz SSS In der nachfolgenden App sind die Schritte zur Konstruktion dargestellt, du musst sie in die richtige Reihenfolge bringen. Übertrage danach die Konstruktion in dein Heft.
2. Schritt: Berechne den Vergrößerungsfaktor k und damit dann b' und c'.
k===1,5; also gilt =1,5
=1,5
b'=1,5·5
b'=7,5 [cm];
ebenso gilt c'=1,5·c = 1,5·6 = 9[cm]3. Schritt: Konstruiere das Dreieck A'B'C' (Konstruktion mit SSS wie oben).
Prüfe deine Lösungen zu S. 97 Nr. 2: Stelle k so ein, dass die jeweiligen Seitenlängen zur Aufgabe passen. Dann lies k und die fehlenden Seitenlängen ab.

k===2; also gilt
=2
=2
b'=2·5
b'=10 [cm];
ebenso gilt c'=2·c = 2·6 = 10[cm]k===1,2; also gilt
=1,2
=1,2
a'=1,2·4
a'=4,8 [cm];
ebenso gilt c'=1,2·c = 1,2·6 = 7,2[cm]Prüfe deine Lösung von S. 97 Nr. 1 a,d:

Prüfe deine Lösung von S. 97 Nr. 3

Umstellen der Formel nach b' k= I∙b
also gilt k∙b = b' (einsetzen und ausrechen)Umstellen der Formel c k= I∙c
k∙c = c' I:k
c = (einsetzen und ausrechnen)zu a) Es gilt k=.
zu b) Die Dreiecke sind ähnlich, also stimmen in drei Winkeln überein. Sie stimmen in zwei Seiten überein, allerdings ist die Reihenfolge der Seiten unterschiedlich (a = b’; b = c’).Bestimme zunächst den Ähnlichkeitsfaktor k mit u und u'. Da der Umfang die Summe der Seitenlängen ist, gilt für den Ähnlichkeitsfaktor k = . Bestimme k (Zwischenergebnis: k=1,5). Damit kannst du nun die Längen des Dreiecks A'B'C' bestimmen.
Du kannst deine Rechnunge wieder mit GeoGebra prüfen:https://www.geogebra.org/classic/qbwddt9zWenn die Seitenlängen mit dem Faktor k vergrößert werden, vergrößert sich der Flächeninhalt mit dem Faktor k². Also gilt k²=4 I
k = 2
Die Seitenlängen werden also jeweils verdoppelt.
3) Strahlensätze
In der Umwelt lassen viele Strecken sich nicht messen, wie z.B. die Höhe von Bäumen oder die Breite eines Sees. Hier hilft die Mathematik!
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen):
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst.
Datei:Dreiecke Konstruktion Einstieg Strahlensätze 2.png
Für die Streckenverhältnisse ergeben sich immer gleiche Werte:
= 0,45
= 0,45
= = 0,6
= = 0,6
= 1,3
= 1,3
= Erinnerung: Das ist der Streckungsfaktor k
= = 2
= = 2
Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c = ; c' = usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die Strahlensätze.
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen.
Die Streckenverhältnisse des ersten Strahlensatz heißen für unsere ähnlichen Dreiecke im Beispiel
==k
Die Streckenverhältnisse des zweiten Strahlensatzes sind in unserem Beispiel entsprechend
==k und ==kZum besseren Verständnis noch einmal links die Erklärung und rechts einige Beispiele in Videos:
Du kannst eine Ergebnisse mithilfe des GeoGebra-Applets prüfen. Stelle dazu die Längen mit den Schiebereglern passend ein.
Um die Strecke einzustellen, nutze den Schieberegler für die Strecke (oder bei Nr. 3 auch Schieberegler für die Strecke ) und verändere diese Länge so lange, bis der passende Wert für die Länge von erscheint.
Die Figur sieht teils anders aus, als die Abbildungen im Buch, entscheidend sind aber nur die Streckenverhältnisse.