Buss-Haskert/Ähnlichkeit und Strahlensätze: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 339: | Zeile 339: | ||
[[Datei:Strahlensatzfigur zu Beispieldreiecken.png]]</div> | [[Datei:Strahlensatzfigur zu Beispieldreiecken.png]]</div> | ||
</div> | </div> | ||
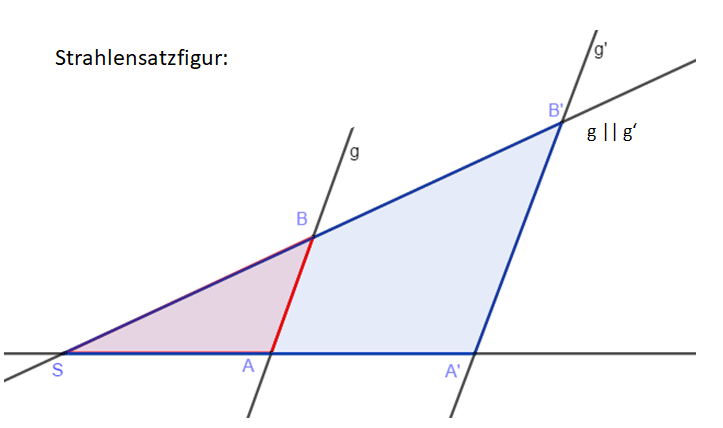
Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c = <math>\ | Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c =<math>\overline{SA}</math> ; c' = <math>\overline{SA'}</math> usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die <b>Strahlensätze</b>. | ||
{{Box|1=HEfteintrag: Die Strahlensätze |2=Werden zwei sich schneidende Geraden von zwei parallelen Geraden geschnitten, entstehen zwei zueinander ähnliche Dreiecke SAB und SA'B'. | {{Box|1=HEfteintrag: Die Strahlensätze |2=Werden zwei sich schneidende Geraden von zwei parallelen Geraden geschnitten, entstehen zwei zueinander ähnliche Dreiecke SAB und SA'B'. | ||
| Zeile 345: | Zeile 345: | ||
[[Datei:Strahlensätze.png]] | [[Datei:Strahlensätze.png]] | ||
Schreibe die Strahlensätze in dein Heft und zeichne auch die Strahlensatzfiguren|3=Arbeitsmethode}} | Schreibe die Strahlensätze in dein Heft und zeichne auch die Strahlensatzfiguren|3=Arbeitsmethode}} | ||
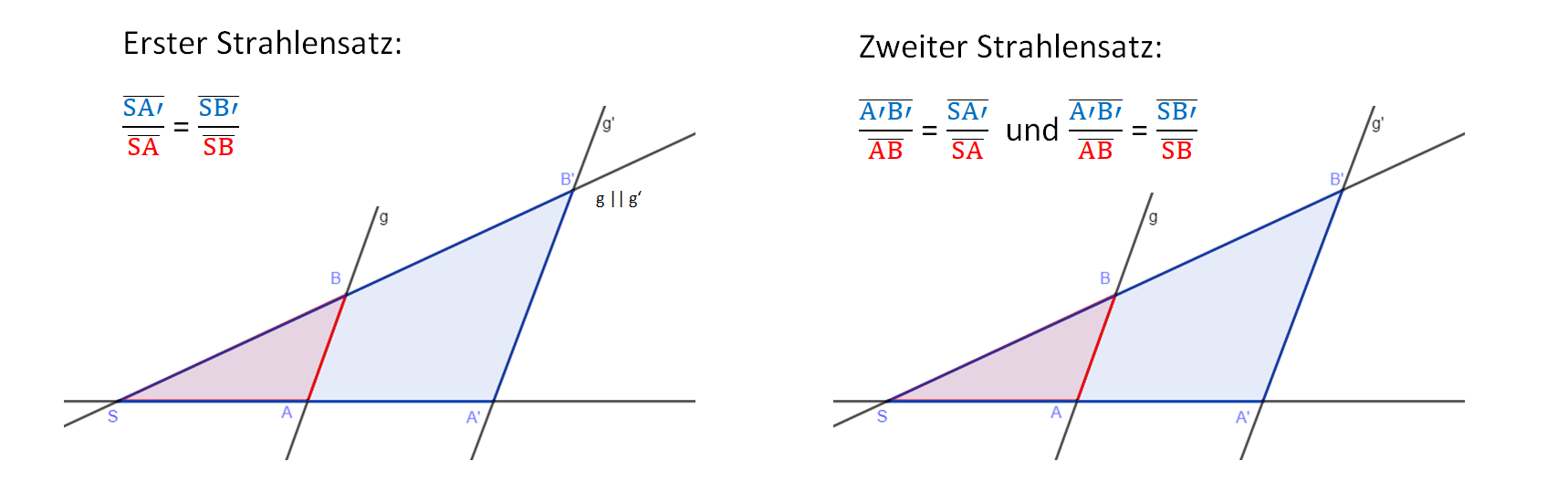
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen. | Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen. | ||
Version vom 6. Mai 2020, 14:32 Uhr
SEITE IM AUFBAU!!
Vorwissen zum Thema Ähnlichkeit
| Du kannst | Übungen im Buch | Übungen online |
|---|---|---|
| -Zahlen runden | S. 90 Nr. 1 |
|
| -Brüche ohne Taschenrechner multiplizieren | S. 90 Nr. 2 |
|
| -Winkel berechnen | S.90 Nr. 3 |
|
| -Größen umwandeln | S. 90 Nr. 4 |
|
| -Umfang und Flächeninhalt von Figuren berechnen | S.90 Nr. 5 |
|
| -Gleichungen und Formeln umstellen | S. 90 Nr. 6,7 |
|
| -Dreiecke konstruieren | S. 90 Nr. 8 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
Ähnlichkeit - Beispiel aus dem Alltag
Das nachfolgende GeoGebra-Applet zeigt zwei Dreiecke, die im geometrischen Sinn ähnlich sind. Bewege die Punkte B und C und beobachte die Größe der Innenwinkel.

Kreuze die richtige Aussage an. (!Wenn man den Punkt C verschiebt, ändern sich nur beim rechten Dreieck die Winkel.) (!Ähnliche Dreiecke haben immer parallele Seiten) (Die Winkel in beiden Dreiecken sind immer gleich groß.) (!Genau ein Winkel in beiden Dreiecken ist gleich groß.)
Und nun untersuche die Seitenlängen der Dreiecke:

1) Vergrößern und Verkleinern
Ein Zeichengerät zum Vergrößern bzw. Verkleinern von Figuren ist der Pantograph. Er wurde früher zum Verkleinern oder Vergrößern von Plänen oder Karten genutzt. Im nachfolgenden Applet kannst du dieses Gerät ausprobieren.
Klicke in das Feld 1 und wähle "Spur ein". Dann ziehe am blauen Punkt. Was passiert?
Kannst du mit dem Feld 2 herausfinden, mit welchem Faktor vergrößert wird?

Das folgende Geogebra-Applet zeigt den Buchstaben T. Verändere die Größe des rechten Buchstaben mithilfe des Schiebereglers.

Welche Bedeutung hat der Schieberegler?
Beim Vergrößern oder Verkleinern einer Figur werden alle Streckenlängen mit demselben Faktor k multipliziert. Dabei ist k immer eine positive Zahl.
Für k > 1 wird die Figur vergrößert.
Für k < 1 wird die Figur verkleinert.
Für die Streckenlängen gilt a' = k∙a, also gilt k = .
Seitenlänge des Originals: a=7cm Seitenlänge des vergrößerten Bildes: a=10,5cm Erinnerung: k = =..., denn a'=k∙a
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=...

Erinnerung: k = ==... (Kürze!)
Für die Breite des vergrößerten Bildes gilt: b'=k∙b=...Setze k ein und berechne.

Beim Vergrößer bzw. verkleinern eines Rechtecks ändert sich der Flächeninhalt mit dem Quadrat des Vergrößerunsfaktors k. Also A' = k²· A.
A = a · b , vergrößere/verkleinere das Rechteck mit dem Faktor k, also a'=k·a und b'=k·b, dann gilt
A’ = a’ · b’ = k·a · k·b = k² · a · b = k² · A
Nutze auch hier das GeoGebra-Applet. Stelle k=71%=0,71 und danach k=141%=1,41 ein. Wie ändert sich der Flächeninhalt?

Wenn k =71% ist, dann wird die Fläche halbiert: f = 0,5.
Wenn k=141% ist, dann wird die Fläche verdoppelt: f = 2.
Erklärung:
A'=k²∙A=0,71²∙A 0,5∙A, denn 0,71²=0,50410,5.
A'=k²∙A=1,41²∙A 2∙A, denn 1,41²=1,98812.Tipp zu b): Bestimme zunächst den Vergrößerungsfaktor k für die Seitenlängen mit k==a':a
29,7 : 25,8 = 1,15 = 115 %, 21 : 19 = 1,10 = 110 %.
Damit alles auf der Seite abgebildet wird, sollte der Kopierer also auf 110 % gestellt werden.
Das GeoGebra-Applet zeigt einen Quader mit a=3cm; b=2cm und c=1cm. Vergrößere die Seitenlängen mit dem Faktor k (Schieberegler). Wie verändert sich das Volumen des Quaders? Notiere V1=6cm³; V2 = 48cm³ = ____ ∙V1; V3 = ... = ____∙V1; usw. Was fällt dir auf?

1=Vergrößert man die Kantenlängen des Quaders mit k, so vergrößert sich das Volumen des Quaders mit k³. Also V' = k³· V.
V = a · b · c , vergrößere/verkleinere die Kantenlängen mit dem Faktor k, also a'=k·a und b'=k·b, c=k·c' dann gilt
V’ = a’· b’· c’= k·a · k·b · k·c = k³ · a · b · c = k³ · V
2) Ähnliche Figuren
Schreibe den Merksatz in dein Heft:

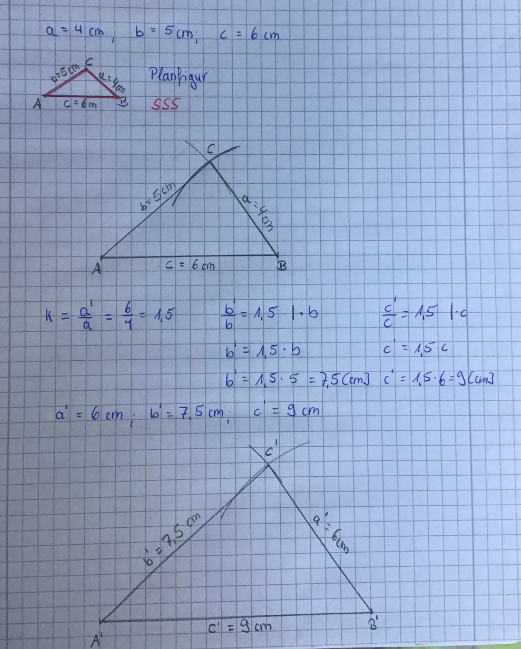
1. Schritt: Konstruiere das Dreieck ABC mit a=4cm; b=5cm und c=6cm. Erinnerung: Kongruenzsatz SSS In der nachfolgenden App sind die Schritte zur Konstruktion dargestellt, du musst sie in die richtige Reihenfolge bringen. Übertrage danach die Konstruktion in dein Heft.
2. Schritt: Berechne den Vergrößerungsfaktor k und damit dann b' und c'.
k===1,5; also gilt =1,5
=1,5
b'=1,5·5
b'=7,5 [cm];
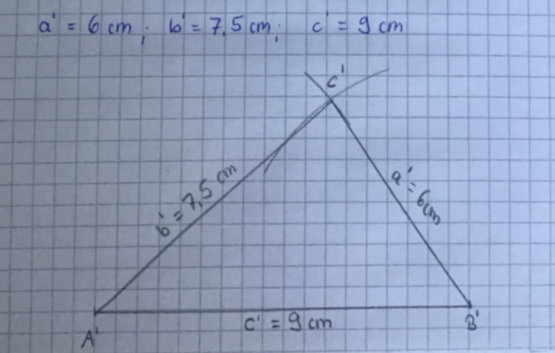
ebenso gilt c'=1,5·c = 1,5·6 = 9[cm]3. Schritt: Konstruiere das Dreieck A'B'C' (Konstruktion mit SSS wie oben).
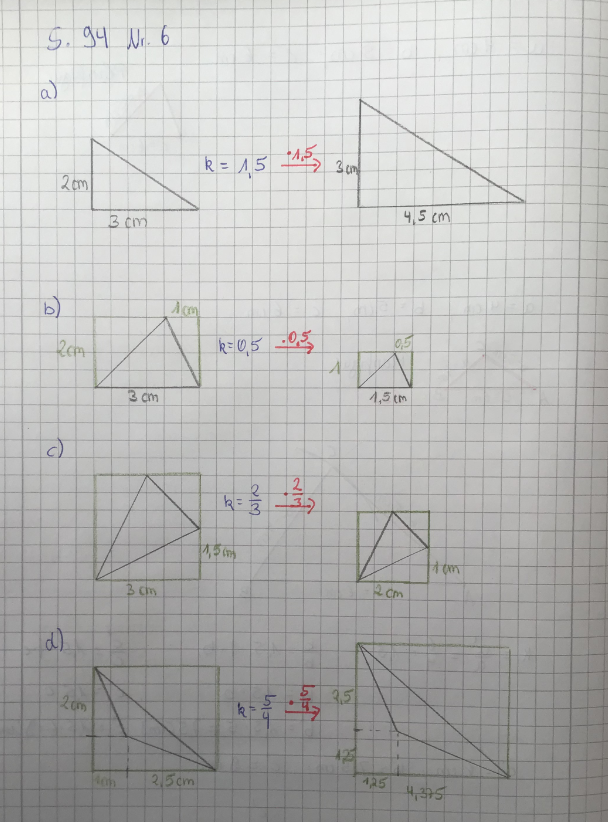
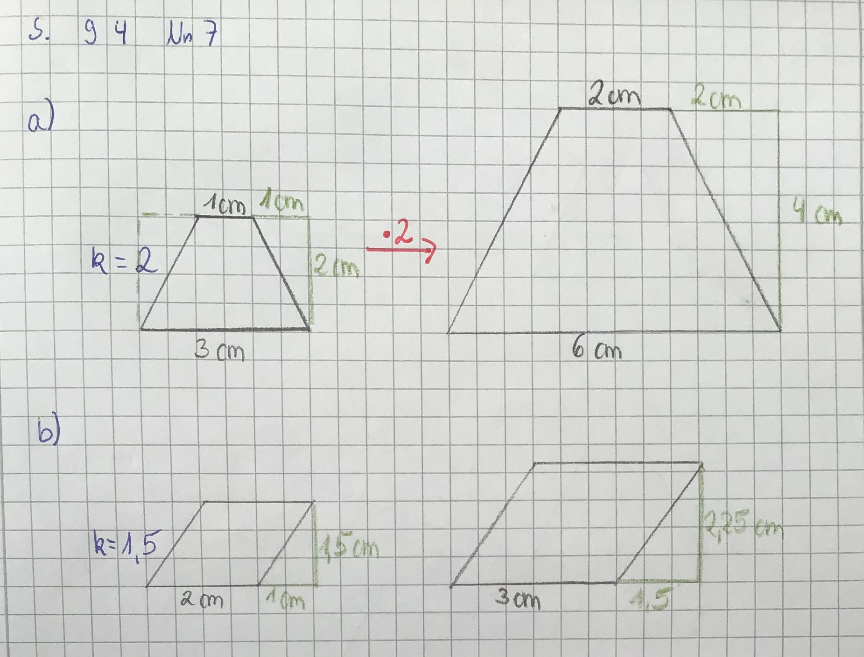
Prüfe deine Lösungen zu S. 97 Nr. 2: Stelle k so ein, dass die jeweiligen Seitenlängen zur Aufgabe passen. Dann lies k und die fehlenden Seitenlängen ab.

k===2; also gilt
=2
=2
b'=2·5
b'=10 [cm];
ebenso gilt c'=2·c = 2·6 = 10[cm]k===1,2; also gilt
=1,2
=1,2
a'=1,2·4
a'=4,8 [cm];
ebenso gilt c'=1,2·c = 1,2·6 = 7,2[cm]Prüfe deine Lösung von S. 97 Nr. 1 a,d:

Prüfe deine Lösung von S. 97 Nr. 3

Umstellen der Formel nach b' k= I∙b
also gilt k∙b = b' (einsetzen und ausrechen)Umstellen der Formel c k= I∙c
k∙c = c' I:k
c = (einsetzen und ausrechnen)zu a) Es gilt k=.
zu b) Die Dreiecke sind ähnlich, also stimmen in drei Winkeln überein. Sie stimmen in zwei Seiten überein, allerdings ist die Reihenfolge der Seiten unterschiedlich (a = b’; b = c’).Bestimme zunächst den Ähnlichkeitsfaktor k mit u und u'. Da der Umfang die Summe der Seitenlängen ist, gilt für den Ähnlichkeitsfaktor k = . Bestimme k (Zwischenergebnis: k=1,5). Damit kannst du nun die Längen des Dreiecks A'B'C' bestimmen.
Du kannst deine Rechnunge wieder mit GeoGebra prüfen:https://www.geogebra.org/classic/qbwddt9zWenn die Seitenlängen mit dem Faktor k vergrößert werden, vergrößert sich der Flächeninhalt mit dem Faktor k². Also gilt k²=4 I
k = 2
Die Seitenlängen werden also jeweils verdoppelt.
3) Strahlensätze
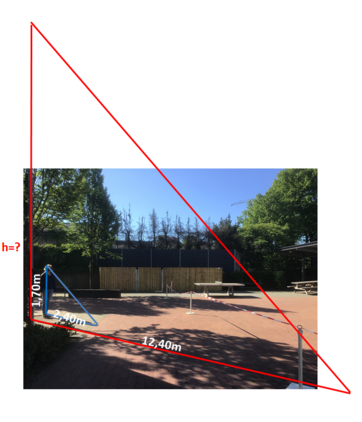
In der Umwelt lassen viele Strecken sich nicht messen, wie z.B. die Höhe von Bäumen oder die Breite eines Sees. Hier hilft die Mathematik!
Wir können mithilfe von Vergleichsstrecken jeweils die Breite bzw. Höhe bestimmen. Wie genau, das lernst du in diesem Kapitel. Wir werden verschiedene Messmethoden kennen lernen, zur "Schattenmethode" sollt ihr schon jetzt Aufgaben selbst zusammenstellen (natürliche ohne sie schon zu lösen):
Nun aber zunächst zu den nötigen mathematischen Fähigkeiten, die du zur Lösung der Aufgaben benötigst.
Datei:Dreiecke Konstruktion Einstieg Strahlensätze 2.png
Für die Streckenverhältnisse ergeben sich immer gleiche Werte:
= 0,45
= 0,45
= = 0,6
= = 0,6
= 1,3
= 1,3
= Erinnerung: Das ist der Streckungsfaktor k
= = 2
= = 2
Der Name "Strahlensatzfigur" wird gewählt, weil die Dreiecksseiten c und b bzw. c' und b' vom Punkt S aus gesehen zwei Strahlen (mit dem Anfangspunkt S) sind. Die parallelen Geraden g und g' sind die Verlängerungen der Seiten a bzw. a'. Die Strahlensätze machen Aussagen über die Streckenverhältnisse, die du oben für die zwei ähnlichen Dreieck aufgestellt hast. Die Bezeichnungen der Strecken ist dann entsprechend der Strahlensatzfigur, also c = ; c' = usw. Die Streckenverhältnisse des Einsteigsbeispiels gelten demnach auch hier. Dies sind die Strahlensätze.
Der erste Strahlensatz mach also Aussagen über die Streckenverhältnisse von Strecken auf den Strahlen, der zweite Strahlensatz über die Streckenverhältnisse von Strecken auf den parallelen Geraden und den Strahlen.
Die Streckenverhältnisse des ersten Strahlensatz heißen für unsere ähnlichen Dreiecke im Beispiel
==k
Die Streckenverhältnisse des zweiten Strahlensatzes sind in unserem Beispiel entsprechend
==k und ==kZum besseren Verständnis noch einmal Erklärungen in Videos: