Benutzer:Florine WWU-6/Optimierungsprobleme: Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Andrea Schellmann verschob die Seite Benutzer:Florine WWU-6/Optimierungsprobleme: Testseite nach Benutzer:Florine WWU-6/Optimierungsprobleme: Testseite: zurückverschieben) |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box-spezial | |||
|Titel= Aufgabe | |||
|Inhalt= 1 2 3 | |||
|Farbe= {{Farbe|links}} | |||
|Icon= {{Vorlage:Icon edit}} | |||
}} | |||
{{Box-spezial | |||
|Titel= Aufgabe | |||
|Inhalt= 1 2 3 | |||
|Farbe= {{Farbe|grün|dunkel}} | |||
|Icon= {{Vorlage:Icon edit}} | |||
}} | |||
{{Box-spezial | |||
|Titel= Aufgabe | |||
|Inhalt= 1 2 3 | |||
|Farbe= {{Farbe|primär|hell}} | |||
|Icon= {{Vorlage:Icon edit}} | |||
}} | |||
{{Box|So löst du Optimierungsprobleme|'''Schritt 1: Erfasse das Problem''' | {{Box|So löst du Optimierungsprobleme|'''Schritt 1: Erfasse das Problem''' | ||
| Zeile 23: | Zeile 52: | ||
# Überprüfe, ob dein Extremwert in deinem gewählten Bereich liegt. | # Überprüfe, ob dein Extremwert in deinem gewählten Bereich liegt. | ||
Da es bei Optimierungsaufgaben um Anwendungssituationen geht, wird kein exakter Wert benötigt. Es reicht also ein guter Näherungswert.|Merke | Da es bei Optimierungsaufgaben um Anwendungssituationen geht, wird kein exakter Wert benötigt. Es reicht also ein guter Näherungswert. | ||
|{{Farbe |links |dunkel}} | |||
|Merke | |||
}} | }} | ||
| Zeile 30: | Zeile 61: | ||
|1= Beispiel | |1= Beispiel | ||
|2='''Aufgabe:''' | |2='''Aufgabe:''' | ||
Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. | ||
Die seitlichen Kurven des Sportplatzes sollen Halbkreise sein. | Die seitlichen Kurven des Sportplatzes sollen Halbkreise sein. | ||
a) Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal? | '''a)''' Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal? | ||
b) Wie groß ist das Fussballfeld? | |||
'''b)''' Wie groß ist das Fussballfeld? | |||
{{Lösung versteckt|2= Lösung | |||
|1= '''Schritt 1:''' | |||
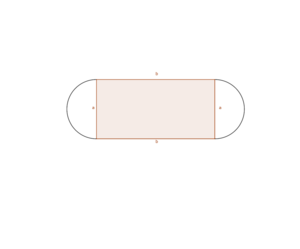
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt <math> A </math> innerhalb des Sportplatzes. | |||
Erstelle eine Skizze dazu: | |||
[[Datei:Skizze .png|mini]] | |||
'''Schritt 2:''' | '''Schritt 2:''' | ||
Die Formel zum Flächeninhalt ist <math>A=2=a | |||
Deine Nebenbedingung findest du im Umfang wieder: U=2 | Die Formel zum Flächeninhalt ist <math>A=2=a \cdot b</math>. Dies ist deine Hauptbedingung.\ | ||
Setze nun deine Nebenbedingung in deine | |||
Deine Nebenbedingung findest du im Umfang wieder: <math>U=2 \cdot a+\pi\cdot b</math>. Diese kannst du nach b umstellen und erhälst: <math>a=\frac{400-\pi \cdot b}{2}</math> | |||
Setze nun deine Nebenbedingung in deine Hauptbedigung ein und erhalte die Zielfunktion: | |||
<math>A(b)=\frac{400-\pi \cdot b}{2}\cdot b=\frac{-\pi \cdot b}{2}+200 \cdot b</math>. | |||
Für diese Funktion kann b nur zwischen 0 und 200 liegen, also <math>0<b<200</math> | |||
'''Schritt 3:''' | |||
Berechne nun deinen Extremwert. Bilde dazu die Ableitungen: | |||
# <math>A'(b)= -\pi \cdot b + 200 \cdot b </math> | |||
# <math> A''(b) = - \pi</math> | |||
Mit der notwendigen Bedingung <math> A'(b)=0</math> erhälst du dann <math> b=\frac{200}{pi} = 63,66 </math>. Mit der hinreichenden Bedindung folgt <math> A''(b)=-\pi \neq 0 </math>, somit erfüllt <math> b </math> alle Bedingungen | |||
Berechne nun <math> a </math> und den Flächeninhalt: | |||
# <math>a=\frac{400-\pi \cdot \frac{200}{pi}}{2} = 100 </math> und | |||
# <math> A = 100 \cdot 63,66 = 6366 m </math> | |||
Der Flächeninhalt des Fussballfeldes kann also mit einer Breite von <math>63,66m</math> und einer Höhe von <math>100m</math> auf <math> 6366 m </math> maximiert werden.}} | |||
|Farbe={{Farbe|grün|dunkel}} | |||
|3=Merke | |3=Merke | ||
}} | }} | ||
Aktuelle Version vom 4. Mai 2020, 07:08 Uhr
| Arbeitsmethode}}