Benutzer:René WWU-6/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 91: | Zeile 91: | ||
{{LearningApp|app=1140264|width=100%|height=400px}} | {{LearningApp|app=1140264|width=100%|height=400px}} | ||
|2=|3=}} | |2=|3=}} | ||
|Arbeitsmethode|Farbe=}} | |Arbeitsmethode|Farbe=}} | ||
| Zeile 120: | Zeile 118: | ||
{{Lösung versteckt|1=Lösung|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Lösung|2=Lösung anzeigen|3=Lösung verbergen}} | ||
{{Lösung versteckt|1=Lösungsweg|2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | {{Lösung versteckt|1=Lösungsweg|2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | ||
|2=|3=}} | |2=|3=}} | ||
| Zeile 180: | Zeile 177: | ||
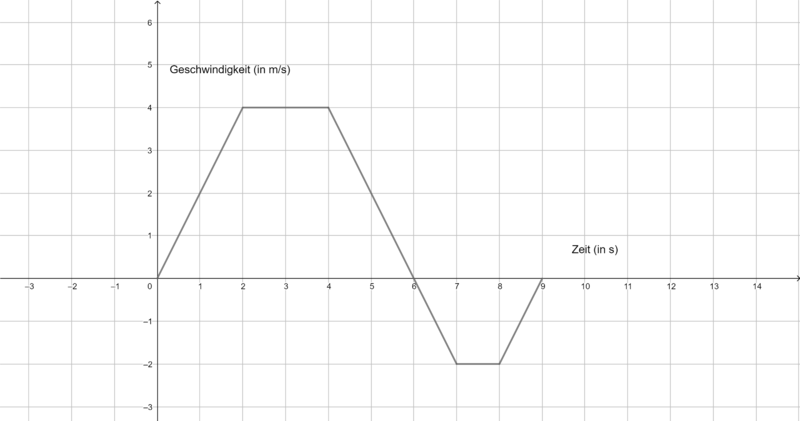
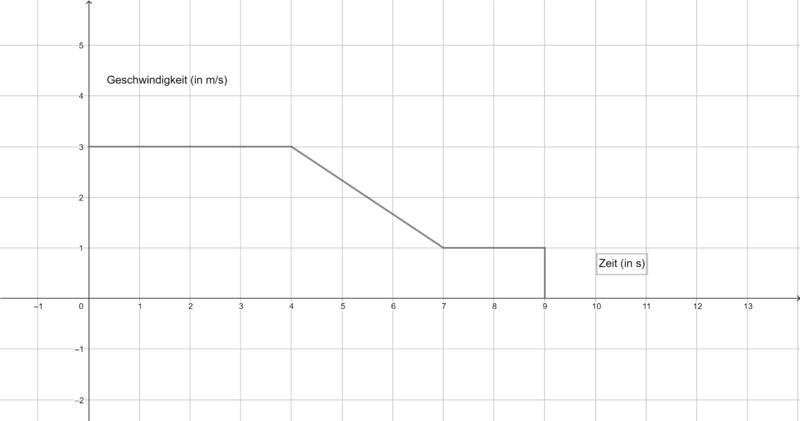
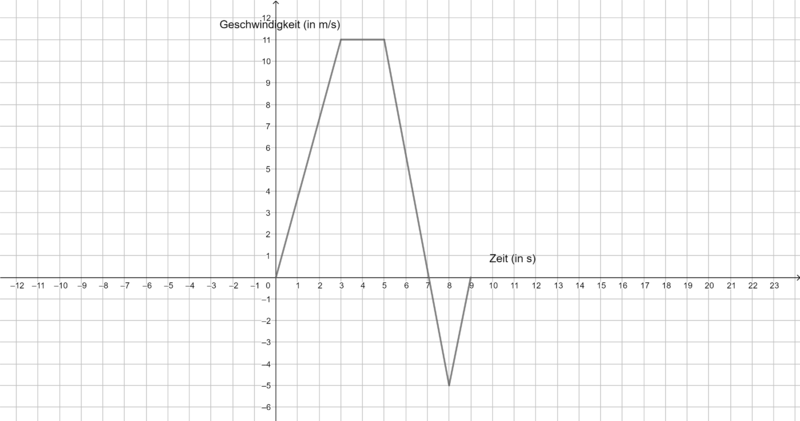
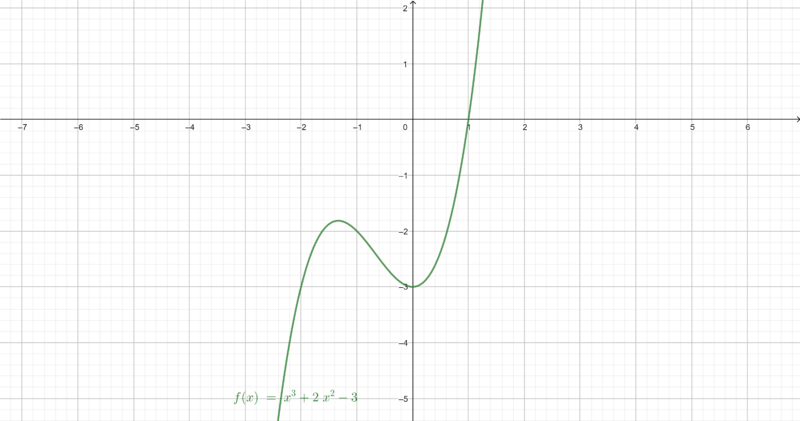
Skizziere eine beliebige Stammfunktion zu folgenden Funktionen auf dem Intervall I=[-5;5]. Zeichne zunächst die Funktion und dann die Stammfunktion auf einen Zettel. Beschreibe dein Vorgehen für charakteristische Punkte (Nullstellen, Extrempunkte, etc.). | Skizziere eine beliebige Stammfunktion zu folgenden Funktionen auf dem Intervall I=[-5;5]. Zeichne zunächst die Funktion und dann die Stammfunktion auf einen Zettel. Beschreibe dein Vorgehen für charakteristische Punkte (Nullstellen, Extrempunkte, etc.). | ||
a)[[Datei:Funktion | a)[[Datei:Funktion g(x).png|mini|800px|center|f(x)=x^(3)+2x^(2)-3]] | ||
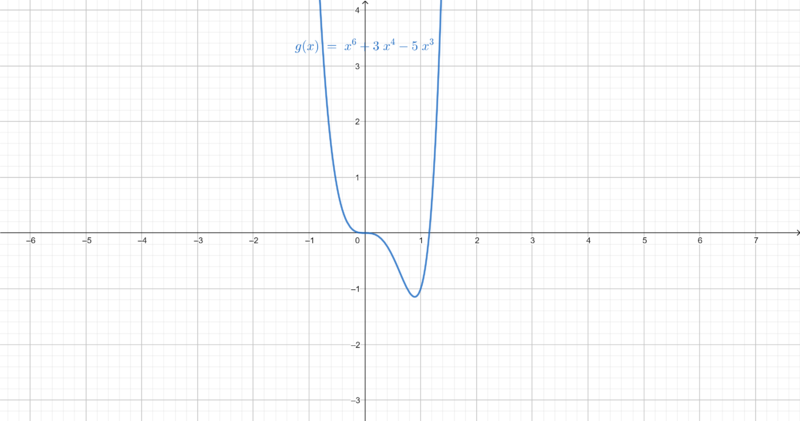
b)[[Datei:Funktion | b)[[Datei:Funktion f(x).png|mini|800px|center|g(x)=x^(6)+3x^(4)-5x^(3)]] | ||
{{Lösung versteckt|1= | |||
|2=Lösung anzeigen|3=Lösung verbergen) | |||
|2=|3=}} | |2=|3=}} | ||
|3=Arbeitsmethode|Farbe=}} | |3=Arbeitsmethode|Farbe=}} | ||
| Zeile 216: | Zeile 219: | ||
|3=Arbeitsmethode|Farbe=}} | |3=Arbeitsmethode|Farbe=}} | ||
{{Box|1=Aufgabe 5|2= | |||
{{Lösung versteckt|1= | |||
Die Funktion f(x)=-x^2+6x gibt die Wachstumsrate von Bakterien an, x in Stunden, f(x) in Hundert Bakterien. Zu Beginn waren 200 Bakterien vorhanden. | |||
* a) Wie lautet die Funktion g(t), die die vorhandene Anzahl von Bakterien zum Zeitpunkt t angibt? | |||
* b) Wie viele Bakterien existieren nach 4 Stunden und nach 6 Stunden? | |||
{{Lösung versteckt|1= | |||
|2=Lösung anzeigen|3=Lösung verbergen) | |||
|2=|3=}} | |||
|3=Arbeitsmethode|Farbe=}} | |||
{{Box|1=Aufgabe 5|2= | |||
{{Lösung versteckt|1= | |||
Bei einem Sprint über 100m treten zwei Läufer gegeneinander an. | |||
Läufer A sprintet mit der Geschwindigkeitsfunktion va(t)=0,25t+10*(1-e^-t). | |||
Läufer B sprintet mit der Geschwindigkeitsfunktion vb(t)=12*(1-e^-t)+c*t^2 | |||
t ist jeweils die Zeit in Sekunden ab dem Start des Laufes und v(t) die Geschwindigkeit der | |||
Läufer in Meter pro Sekunde. | |||
* a) Geben sie die Funktionen an, die die zurückgelegte Strecke zum Zeitpunkt t angibt. | |||
* b) Zeige, dass Läufer A ungefähr 9,8 Sekunden benötigt. | |||
* c) Bestimme den Wert von c so, dass der Läufer nach 9,69 Sekunden ins Ziel kommt. | |||
* d) wie viel Meter sind die beiden Läufer nach 5 s von einander entfernt? | |||
{{Lösung versteckt|1= | |||
|2=Lösung anzeigen|3=Lösung verbergen) | |||
|2=|3=}} | |||
|3=Arbeitsmethode|Farbe=}} | |||
<br /> | <br /> | ||
Version vom 21. April 2020, 15:40 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
Kombinationen
Integral: Rekonstruieren von Größen
{{Box|1=Aufgabe 5|2=
Skizziere eine beliebige Stammfunktion zu folgenden Funktionen auf dem Intervall I=[-5;5]. Zeichne zunächst die Funktion und dann die Stammfunktion auf einen Zettel. Beschreibe dein Vorgehen für charakteristische Punkte (Nullstellen, Extrempunkte, etc.).
a) b)
{{Box|1=Aufgabe 5|2=
Die Funktion f(x)=-x^2+6x gibt die Wachstumsrate von Bakterien an, x in Stunden, f(x) in Hundert Bakterien. Zu Beginn waren 200 Bakterien vorhanden.
- a) Wie lautet die Funktion g(t), die die vorhandene Anzahl von Bakterien zum Zeitpunkt t angibt?
- b) Wie viele Bakterien existieren nach 4 Stunden und nach 6 Stunden?
{{Box|1=Aufgabe 5|2=
Bei einem Sprint über 100m treten zwei Läufer gegeneinander an. Läufer A sprintet mit der Geschwindigkeitsfunktion va(t)=0,25t+10*(1-e^-t). Läufer B sprintet mit der Geschwindigkeitsfunktion vb(t)=12*(1-e^-t)+c*t^2 t ist jeweils die Zeit in Sekunden ab dem Start des Laufes und v(t) die Geschwindigkeit der Läufer in Meter pro Sekunde.
- a) Geben sie die Funktionen an, die die zurückgelegte Strecke zum Zeitpunkt t angibt.
- b) Zeige, dass Läufer A ungefähr 9,8 Sekunden benötigt.
- c) Bestimme den Wert von c so, dass der Läufer nach 9,69 Sekunden ins Ziel kommt.
- d) wie viel Meter sind die beiden Läufer nach 5 s von einander entfernt?