Benutzer:René WWU-6/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 5: | Zeile 5: | ||
====Vorlagen==== | ====Vorlagen==== | ||
{{Lösung versteckt|Ganz | {{Lösung versteckt|Ganz per Mausklick aktivierbar|Versteckte Hinweise und Lösungen|Versteckte Hinweise und Lösungen}} | ||
{{Box|Aufgabe|Dies ist eine Aufgabe|Arbeitsmethode}} | {{Box|Aufgabe|Dies ist eine Aufgabe|Arbeitsmethode}} | ||
{{Box|Übung|Dies ist eine Übung|Üben}} | {{Box|Übung|Dies ist eine Übung|Üben}} | ||
| Zeile 28: | Zeile 28: | ||
[[File:Kapitolinischer Pythagoras adjusted.jpg|thumb|Herme des (um 120 n. Chr.); Kapitolinische Museen, Rom|alternativtext=|zentriert]] | [[File:Kapitolinischer Pythagoras adjusted.jpg|thumb|Herme des (um 120 n. Chr.); Kapitolinische Museen, Rom|alternativtext=|zentriert]] | ||
==Integral: Rekonstruieren von Größen== | ==Integral: Rekonstruieren von Größen== | ||
{{Box|Beispiel| | {{Box|Beispiel| | ||
{{Lösung versteckt|1= | |||
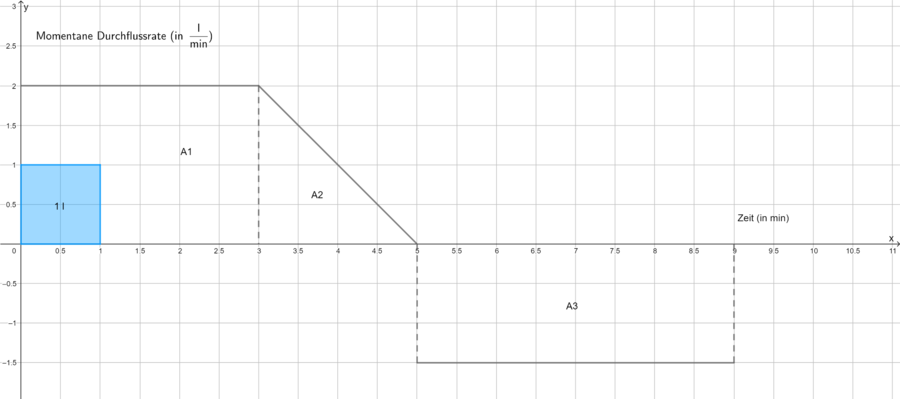
Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur ist die momentane Durchflussrate f der Leitung für das Intervall [0;9] dargestellt. | Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur ist die momentane Durchflussrate f der Leitung für das Intervall [0;9] dargestellt. | ||
[[Datei:Durchflussrate Figur 1.png|alternativtext=Beispielaufgabe|mini|900px|center|Figur 1]] | [[Datei:Durchflussrate Figur 1.png|alternativtext=Beispielaufgabe|mini|900px|center|Figur 1]] | ||
Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank? | Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank? | ||
{{Lösung versteckt|Es befinden sich nach 9 min 2 Liter im Wassertank.|Lösung anzeigen|Lösung verbergen}} | {{Lösung versteckt|Es befinden sich nach 9 min 2 Liter im Wassertank.|Lösung anzeigen|Lösung verbergen}} | ||
{{Lösung versteckt| | {{Lösung versteckt|1= | ||
1=Im Intervall [0;3] beträgt der Zufluss <math>2\frac{l}{min}</math>. In diesen 3 Minuten fließen <math>2 \frac{l}{min} \cdot 3\ min = 6 l </math> in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate <math>1\frac{l}{min}</math>. In diesen 2 Minuten kommen <math>1 \frac{l}{min} \cdot 2\ min = 2 l </math> dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen <math>1,5 \frac{l}{min} \cdot 4\ min = 6 l </math> ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser '''orientierte Flächeninhalt''' beträgt beim Wassertank: | |||
Im Intervall [0;3] beträgt der Zufluss <math>2\frac{l}{min}</math>. In diesen 3 Minuten fließen <math>2 \frac{l}{min} \cdot 3\ min = 6 l </math> in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate <math>1\frac{l}{min}</math>. In diesen 2 Minuten kommen <math>1 \frac{l}{min} \cdot 2\ min = 2 l </math> dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen <math>1,5 \frac{l}{min} \cdot 4\ min = 6 l </math> ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser '''orientierte Flächeninhalt''' beträgt beim Wassertank: | |||
A1 + A2 - A3 = 2 Flächeneinheiten | A1 + A2 - A3 = 2 Flächeneinheiten | ||
und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank. | und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank. | ||
|2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | |2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | ||
|2=Beispiel anzeigen|3=Beispiel verbergen}} | |||
|Merke|Farbe= #FF4500 }} | |Merke|Farbe= #FF4500 }} | ||
{{Box|Merke|Ist der Graph einer momentanen Änderungsrate aus gradlinigen Teilstücken zusammengesetzt, so kann man die '''Gesamtänderung''' der Größe (Wirkung) rekonstruieren, indem man den orientierten Flächeninhalt zwischen den Graphen der momentanen Änderungsrate und der x-Achse bestimmt. Den orientierten Flächeninhalt nennt man auch das bestimmte Integral.|Merke|Farbe= #9B30FF}} | |||
{{Box|Merke| | |||
Ist der Graph einer momentanen Änderungsrate aus gradlinigen Teilstücken zusammengesetzt, so kann man die '''Gesamtänderung''' der Größe (Wirkung) rekonstruieren, indem man den orientierten Flächeninhalt zwischen den Graphen der momentanen Änderungsrate und der x-Achse bestimmt. Den orientierten Flächeninhalt nennt man auch das bestimmte Integral. | |||
|Merke|Farbe= #9B30FF}} | |||
{{Lösung versteckt|1=1|2=2|3=3}} | |||
{{Box|Aufgabe 1| | {{Box|Aufgabe 1| | ||
{{Lösung versteckt|1= | |||
Du erkennst, dass der orientierte Flächeninhalt nicht mit dem Wert des Flächeninhalt zwischen Graph und x-Achse übereinstimmt. Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten. | Du erkennst, dass der orientierte Flächeninhalt nicht mit dem Wert des Flächeninhalt zwischen Graph und x-Achse übereinstimmt. Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten. | ||
{{LearningApp|app=1140264|width=100%|height=400px}} | {{LearningApp|app=1140264|width=100%|height=400px}} | ||
|2=Aufgabe anzeigen|3=Aufgabe verbergen}} | |||
|Arbeitsmethode|Farbe=}} | |Arbeitsmethode|Farbe=}} | ||
| Zeile 59: | Zeile 99: | ||
{{Box|Aufgabe 3| | {{Box|Aufgabe 3| | ||
{{Lösung versteckt|1= | |||
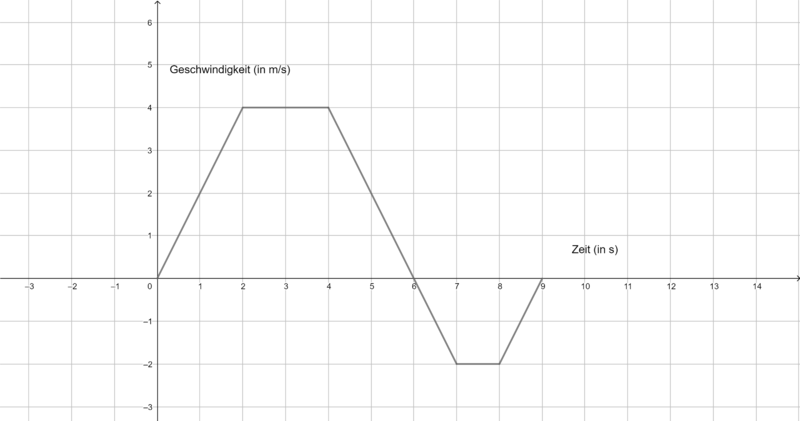
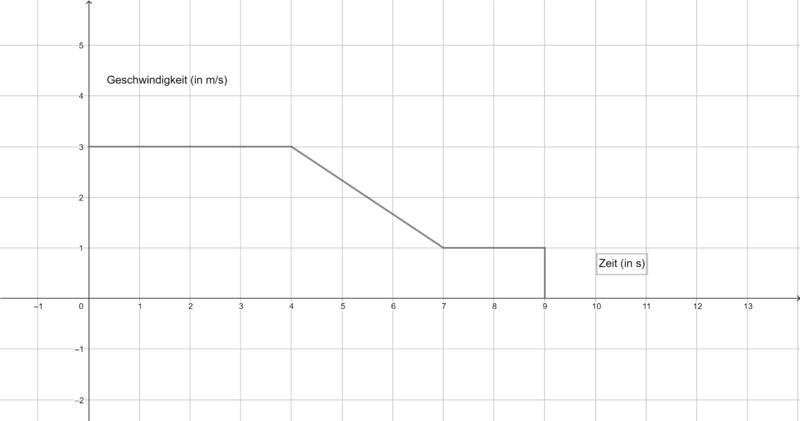
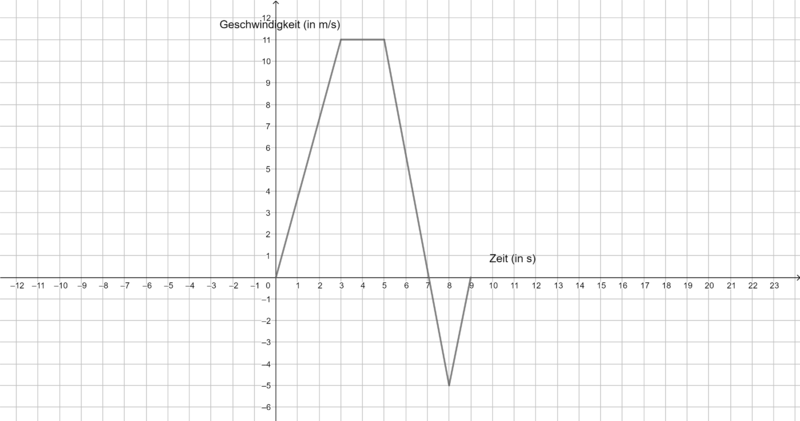
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | ||
| Zeile 76: | Zeile 119: | ||
{{Lösung versteckt|1=Lösungsweg|2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | {{Lösung versteckt|1=Lösungsweg|2=Lösungsweg anzeigen|3=Lösungweg verbergen}} | ||
|2=Aufgabe anzeigen|3=Aufgabe verbergen}} | |||
|Arbeitsmethode|Farbe=#FFFF00}} | |Arbeitsmethode|Farbe=#FFFF00}} | ||
| Zeile 81: | Zeile 126: | ||
{{Box|1=Beachte|2= | {{Box|1=Beachte|2= | ||
{{Lösung versteckt|1= | |||
Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden. | Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden. | ||
| Zeile 92: | Zeile 139: | ||
Was fällt dir auf? Wo besteht der Zusammenhang zwischen der Funktion und seiner Stammfunktion? Wo sind charakteristische Punkte? | Was fällt dir auf? Wo besteht der Zusammenhang zwischen der Funktion und seiner Stammfunktion? Wo sind charakteristische Punkte? | ||
|2=Aufgabe anzeigen|3=Aufgabe verbergen}} | |||
|3=Merke|Farbe=#FFFF00}} | |3=Merke|Farbe=#FFFF00}} | ||
{{Box|1= | {{Box|1=Merksatz|2= | ||
{{Lösung versteckt|1= | |||
Eine Funktion F heißt '''Stammfunktion ''' zu einer Funktion f auf einem Intervall I, wenn für alle x in I gilt: | Eine Funktion F heißt '''Stammfunktion ''' zu einer Funktion f auf einem Intervall I, wenn für alle x in I gilt: | ||
| Zeile 103: | Zeile 154: | ||
F(x) = G(x)+c | F(x) = G(x)+c | ||
|Farbe=}} | |2=|3=}} | ||
3=Merke|Farbe=}} | |||
{{Box|Aufgabe 4| | {{Box|Aufgabe 4| | ||
{{Lösung versteckt|1= | |||
Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten | Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten | ||
{{LearningApp|app=1689396|width=100%|height=400px}} | {{LearningApp|app=1689396|width=100%|height=400px}} | ||
|2=|3=}} | |||
|Arbeitsmethode|Farbe=#FFFF00}} | |Arbeitsmethode|Farbe=#FFFF00}} | ||
Version vom 21. April 2020, 13:52 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz per Mausklick aktivierbar
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
Kombinationen
Integral: Rekonstruieren von Größen
1
Satz: Stammfunktionen bestimmen (Buch S. 68)
Beispiel: Stammfunktion bestimmen
Aufgabe:
Aufgabe: Bestimme eine Stammfunktion folgender Funktionen:
2 Textaufgaben: