Benutzer:René WWU-6/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 58: | Zeile 58: | ||
{{Box|Aufgabe 2| | {{Box|Aufgabe 2| | ||
Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten. | |||
{{LearningApp|app=3978880|width=100%|height=400px}} | |||
|Arbeitsmethode|Farbe=}} | |||
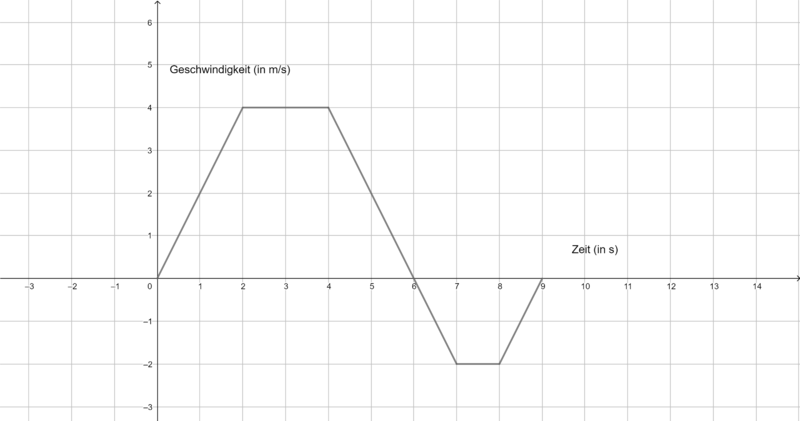
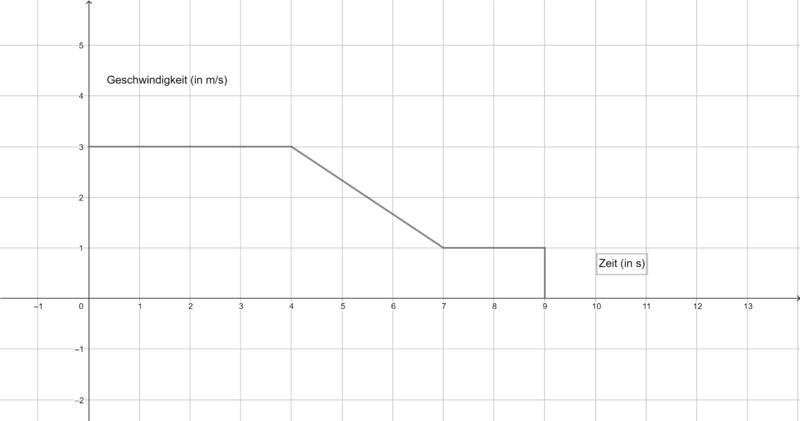
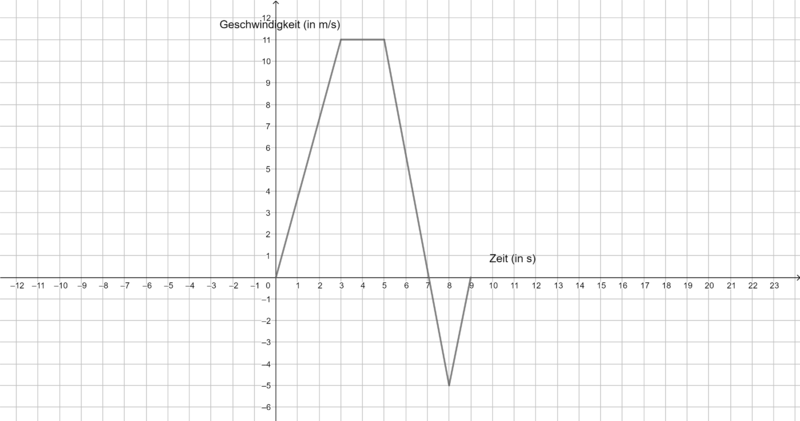
{{Box|Aufgabe 3| | |||
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | ||
| Zeile 79: | Zeile 88: | ||
{{Box|Aufgabe | {{Box|Beachte| | ||
Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden. | |||
# 1) f(x)=1 | |||
2) f(x)=x | |||
3) f(x)=x^2 | |||
|Hervorhebung1|Farbe=}} | |||
{{Box|Aufgabe 4| | |||
Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten. | Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten. | ||
| Zeile 102: | Zeile 125: | ||
{{LearningApp|app=1141792|width=100%|height=400px}} | {{LearningApp|app=1141792|width=100%|height=400px}} | ||
{{LearningApp|app=4942220|width=100%|height=400px}} | {{LearningApp|app=4942220|width=100%|height=400px}} | ||
Version vom 19. April 2020, 11:48 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz einfach per Mausklick aktivierbar
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
Kombinationen
a^2+b^2=c^2
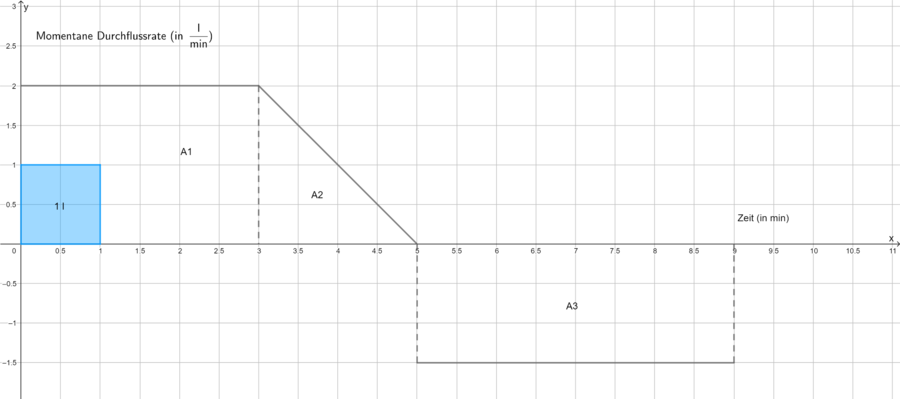
Integral: Rekonstruieren von Größen