Benutzer:René WWU-6/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 47: | Zeile 47: | ||
|Merke|Farbe= #FF4500 }} | |Merke|Farbe= #FF4500 }} | ||
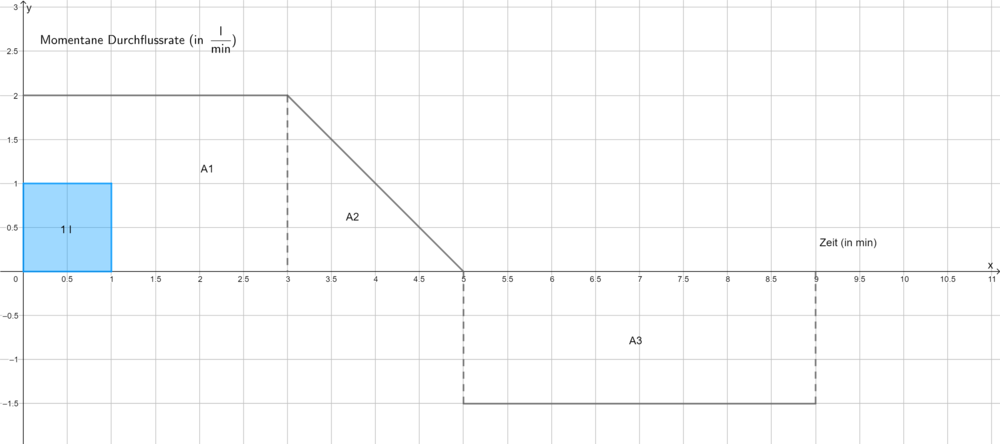
{{Box|Merke|Ist der Graph einer momentanen Änderungsrate aus gradlinigen Teilstücken zusammengesetzt, so kann man die '''Gesamtänderung''' der Größe (Wirkung) rekonstruieren, indem man den orientierten Flächeninhalt zwischen den Graphen der momentanen Änderungsrate und der x-Achse bestimmt.|Merke|Farbe= #9B30FF}} | {{Box|Merke|Ist der Graph einer momentanen Änderungsrate aus gradlinigen Teilstücken zusammengesetzt, so kann man die '''Gesamtänderung''' der Größe (Wirkung) rekonstruieren, indem man den orientierten Flächeninhalt zwischen den Graphen der momentanen Änderungsrate und der x-Achse bestimmt. Den orientierten Flächeninhalt nennt man auch das bestimmte Integral.|Merke|Farbe= #9B30FF}} | ||
| Zeile 53: | Zeile 53: | ||
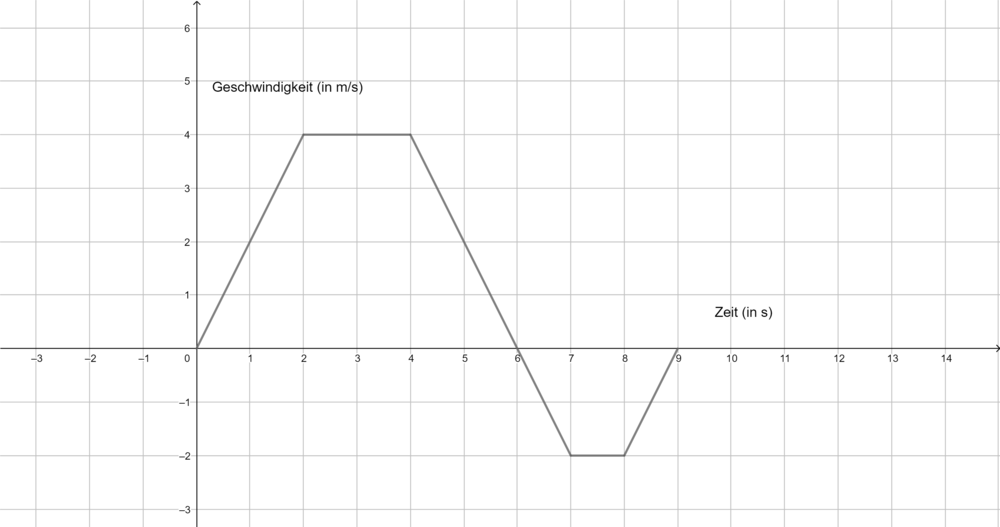
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren. | ||
a) [[Datei:1a Bild.png|alternativtext=Aufgabe 1 a)|mini|Aufgabe 1 a)]] | a) [[Datei:1a Bild.png|alternativtext=Aufgabe 1 a)|mini|1000px|Aufgabe 1 a)]] | ||
{{Lösung versteckt|1=Lösung|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Lösung|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 70: | Zeile 70: | ||
|Arbeitsmethode|Farbe=#FFFF00}} | |Arbeitsmethode|Farbe=#FFFF00}} | ||
{{Box|Aufgabe 2| | |||
Dies ist eine Aufgabe | |||
|Arbeitsmethode|Farbe=}} | |||
Version vom 19. April 2020, 11:22 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz einfach per Mausklick aktivierbar
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
Kombinationen
a^2+b^2=c^2
Integral: Rekonstruieren von Größen