Benutzer:René WWU-6/Testseite: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Markierung: 2017-Quelltext-Bearbeitung
Zeile 37: Zeile 37:
{{Lösung versteckt|Es befinden sich 2 Liter im Wassertank|Lösung anzeigen|Lösung verbergen}}
{{Lösung versteckt|Es befinden sich 2 Liter im Wassertank|Lösung anzeigen|Lösung verbergen}}


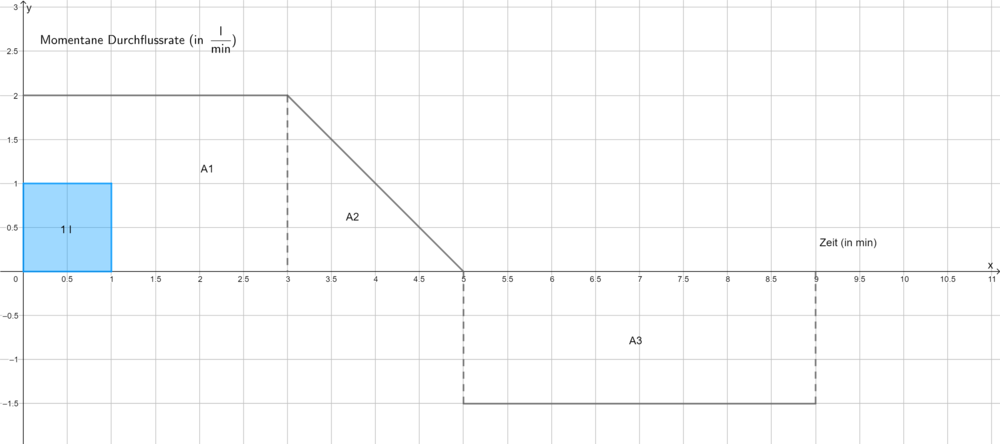
{{Lösung versteckt|1=Im Intervall [0;3] beträgt der Zufluss <math>2\frac{l}{min}</math>. In diesen 3 Minuten fließen <math>2 \frac{l}{min} \cdot 3\ min = 6 l </math> in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate <math>1\frac{l}{min}</math>. In diesen 2 Minuten kommen <math>1 \frac{l}{min} \cdot 2\ min = 2 l </math> dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen <math>1,5 \frac{l}{min} \cdot 4\ min = 6 l </math> ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser '''orientierte Flächeninhalt''' beträgt beim Wassertank: A1 + A2 - A3 = 2 Flächeneinheiten und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank.|2=Lösungsweg anzeigen|3=Lösungweg verbergen}}
{{Lösung versteckt|1=Im Intervall [0;3] beträgt der Zufluss <math>2\frac{l}{min}</math>. In diesen 3 Minuten fließen <math>2 \frac{l}{min} \cdot 3\ min = 6 l </math> in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate <math>1\frac{l}{min}</math>. In diesen 2 Minuten kommen <math>1 \frac{l}{min} \cdot 2\ min = 2 l </math> dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen <math>1,5 \frac{l}{min} \cdot 4\ min = 6 l </math> ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser '''orientierte Flächeninhalt''' beträgt beim Wassertank:  
A1 + A2 - A3 = 2 Flächeneinheiten  
und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank.|2=Lösungsweg anzeigen|3=Lösungweg verbergen}}
|Merke|Farbe={{Farbe|red|dunkel}}}}
|Merke|Farbe={{Farbe|red|dunkel}}}}
<br />
<br />

Version vom 18. April 2020, 18:16 Uhr

Spielwiese

Schreiben im Wiki

Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.

Vorlagen

Ganz einfach per Mausklick aktivierbar
Aufgabe
Dies ist eine Aufgabe
Übung
Dies ist eine Übung
Merksatz
Dies ist ein Merksatz

Dateien

Bild aus ZUM Projekte:

Basketball

Bild aus Wikipedia:

Löwe (Panthera leo)
Löwe (Panthera leo)


Interaktive Applets


Kombinationen

Aufgabe
Bearbeite folgende Aufgabe


a^2+b^2=c^2
Herme des Pythagoras (um 120 n. Chr.); Kapitolinische Museen, Rom

Integral: Rekonstruieren von Größen

Beispiel

Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur 1 ist die momentane Durchflussrate f der Leitung für das Intervall [0;9] dargestellt.

Durchflussrate Figur 1.png

Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank?

Es befinden sich 2 Liter im Wassertank

Im Intervall [0;3] beträgt der Zufluss . In diesen 3 Minuten fließen in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate . In diesen 2 Minuten kommen dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser orientierte Flächeninhalt beträgt beim Wassertank: A1 + A2 - A3 = 2 Flächeneinheiten

und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank.


Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:René_WWU-6/Testseite&oldid=19104“