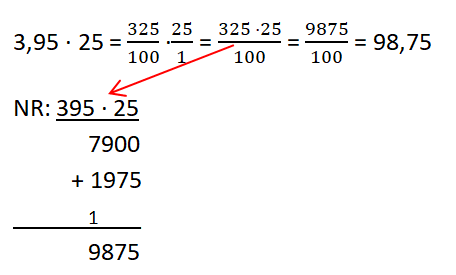Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/2) Dezimalbrüche multiplizieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 22: | Zeile 22: | ||
{{#ev:youtube|vXMpqJ2dZbs}} | {{#ev:youtube|vXMpqJ2dZbs}} | ||
{{Box|Übung: Multiplizieren mit Zehnerpotenzen|Bearbeite die | {{Box|Übung: Multiplizieren mit Zehnerpotenzen|Bearbeite die folgende App und danach S. 124 Nr. 3 im Heft.|Übung}} | ||
{{h5p|id=796832|height=300}} | {{h5p|id=796832|height=300}} | ||
| Zeile 58: | Zeile 58: | ||
{{Lösung versteckt| Lösungswort: KROATIEN|Lösungswort Nr. 5|Verbergen}} | {{Lösung versteckt| Lösungswort: KROATIEN|Lösungswort Nr. 5|Verbergen}} | ||
{{Lösung versteckt| Beispiel für den Überschlag: a) 30 · 7 = 210; | {{Lösung versteckt|1=Beispiel für den Überschlag: a) 30 · 7 = 210; | ||
b) 0,03 · 12 = 0,36; d) 170 · 0,1 = 17 |Nr. 6 Beispiele für den Überschlag|Verbergen}} | b) 0,03 · 12 = 0,36; d) 170 · 0,1 = 17 |2=Nr. 6 Beispiele für den Überschlag|3=Verbergen}} | ||
Wo finden wir weitere Beispiele zur Multiplikation von Dezimalbrüchen im Sport? | Wo finden wir weitere Beispiele zur Multiplikation von Dezimalbrüchen im Sport? | ||
| Zeile 67: | Zeile 67: | ||
{{Box|Übung 3 |Berechne S. 130 Nr. 16, 17 und 21. Denke an eine übersichtliche Darstellung. | {{Box|Übung 3 |Berechne S. 130 Nr. 16, 17 und 21. Denke an eine übersichtliche Darstellung. | ||
geg:… | geg:… | ||
ges:… | ges:… | ||
R:… | R:… | ||
Antwort:…|Üben}} | Antwort:…|Üben}} | ||
{{Lösung versteckt| Flächeninhalt eines Rechtecks A = a · b. Multipliziere schriftlich, denke an das Komma im Ergebnis| Tipp zu Nr. 16|Verbergen}} | {{Lösung versteckt|1=Flächeninhalt eines Rechtecks A = a · b. Multipliziere schriftlich, denke an das Komma im Ergebnis|2=Tipp zu Nr. 16|3=Verbergen}} | ||
{{Lösung versteckt| Ergänze die linke Figur zu einer großen Fläche und subtrahiere dann das zu viel berechnete Rechteck| Tipp zu Nr. 17|Verbergen}} | {{Lösung versteckt| Ergänze die linke Figur zu einer großen Fläche und subtrahiere dann das zu viel berechnete Rechteck| Tipp zu Nr. 17|Verbergen}} | ||
{{Lösung versteckt| Berechne zunächst das Volumen des Beckens (des Quaders) mit V = a · b · c , wobei c hier die Wassertiefe ist.|Tipp zu Nr. 21 a)}} | {{Lösung versteckt|1=Berechne zunächst das Volumen des Beckens (des Quaders) mit V = a · b · c , wobei c hier die Wassertiefe ist.|2=Tipp zu Nr. 21 a)|3=Verbergen}} | ||
{{Lösung versteckt| Berechne zunächst das Volumen des abgeflossenen Wassers mit V = a · b · c , wobei c hier die Höhe ist, um die der Wasserspiegel gesunken ist.|Tipp zu Nr. 21 b)}} | {{Lösung versteckt|1=Berechne zunächst das Volumen des abgeflossenen Wassers mit V = a · b · c , wobei c hier die Höhe ist, um die der Wasserspiegel gesunken ist.|2=Tipp zu Nr. 21 b)|3=Verbergen}} | ||
{{Lösung versteckt| Berechne die Fläche, die gefliest werden muss. Dies ist die Oberfläche eines Quaders, aber ohne die obere Fläche (die Deckfläche fehlt).|Tipp zu Nr. 21 c)}} | {{Lösung versteckt|1=Berechne die Fläche, die gefliest werden muss. Dies ist die Oberfläche eines Quaders, aber ohne die obere Fläche (die Deckfläche fehlt).|2=Tipp zu Nr. 21 c)|3=Verbergen}} | ||
{{Box|Weitere Anwendungen|Vielfältige Anwendungen ergeben sich bei Berechnungen in Wohnungen. Löse S. 130 Nr. 16.|Üben}} | {{Box|Weitere Anwendungen|Vielfältige Anwendungen ergeben sich bei Berechnungen in Wohnungen. Löse S. 130 Nr. 16.|Üben}} | ||
Version vom 13. April 2020, 08:00 Uhr
Eine weitere Frage, die wir zu Beginn an die Weitsprungergebnisse beim Sportabzeichentag gestellt haben, war folgende:
Wenn du den besten Sprung betrachtest, wie weit kämst du dann mit 25 Sprüngen für die gesamte Klasse?
Nehmen wir noch einmal die Ergebnisse von Tom: 3m; 3,2m und 3,95m.
Die Rechnung heißt hier also: 3,95 m · 25
Um dies beantworten zu können, müssen wir Dezimalbrüche multiplizieren können. Dies lernst du auf dieser Seite.
Beginnen wir mit einer leichteren Frage:
Das kannst du sicher im Kopf berechnen. Fällt dir etwas auf?
Schau das Erklärvideo on:
Wie können wir nun die Frage beantworten, wie weit die gesamte Klasse mit dem besten Sprung von Tom gesprungen wäre?
Wir müssen 3,95m · 25 rechnen.
Idee 2: Wir können Brüche multiplizieren, dies übertragen wir nun:
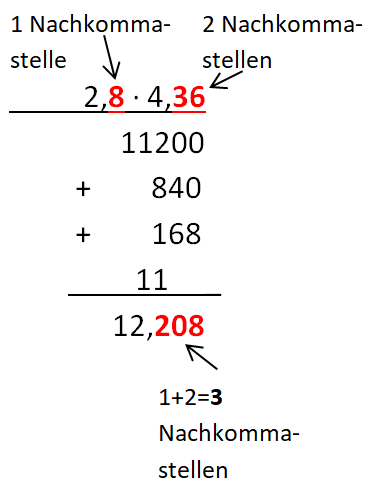
Geht das auch mit zwei Dezimalbrüchen?
Das Video fasst die Regel noch einmal zusammen:
Beispiel für den Überschlag: a) 30 · 7 = 210;
b) 0,03 · 12 = 0,36; d) 170 · 0,1 = 17Wo finden wir weitere Beispiele zur Multiplikation von Dezimalbrüchen im Sport?
Wir gehen schwimmen. Das Becken ist 28,5 m lang und 21,6 m breit. Welche Fläche hat der Beckenboden?