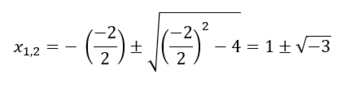|
|
| (19 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | Quelltext aus [[Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Terme und Gleichungen|Terme und Gleichungen]]: |
| | {{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> |
| | <span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> |
| | <span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> |
| | |
| | {{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} |
| | |
| | {{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel |
| | |
| | <math> x_{1,2} = - \frac{-2}{2} \pm \sqrt{\left( \frac{-2}{2} \right) ^2 -4}= 1 \pm \sqrt{-3}</math> |
| | |
| | , so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. <br /> '''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} |
| | |
| | |3=Arbeitsmethode }} |
| | |
| | Nicht verstandene Mathe-Formel durch Foto ersetzt: |
| | {{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> |
| | <span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> |
| | <span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> |
| | |
| | {{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} |
| | |
| | {{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. |
| | |
| | [[Datei:TG Lösung zu A7.3a.png|350px|Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)]] |
| | |
| | '''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} |
| | |
| | |3=Arbeitsmethode }} |
| | |
| | |
| ===Spielwiese=== | | ===Spielwiese=== |
|
| |
|
| Zeile 110: |
Zeile 141: |
| |2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | | |2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} |
| |Arbeitsmethode}} | | |Arbeitsmethode}} |
|
| |
| ===Fragen zum Quelltext===
| |
|
| |
| ====Frage 1====
| |
| {{Box|Aufgabe 3: Wie lautet die Gleichung der Geraden?|Gegeben sei die Steigung der Geraden <math>m = 3,5</math>. Außerdem verlaufe die Gerade durch den Punkt <math>P(2/5)</math>. Bestimme die Gleichung der Geraden in der Form <math>f(x) = mx + b</math>.
| |
|
| |
| <!-- <iframe src="https://learningapps.org/watch?v=p0cp6e2a319" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> funktioniert nicht, nutze stattdessen:-->
| |
|
| |
| {{LearningApp|width:100%|height:700px|app=p0cp6e2a319}}
| |
| |Arbeitsmethode}}
| |
|
| |
| ====Frage 2====
| |
|
| |
| a) <math>9x+9y+9z</math>
| |
|
| |
| b) <math>81x+45y</math>
| |
|
| |
| c) <math>5x-4xy+9xz+</math>
| |
|
| |
| d) <math>25a-35ab+50ax</math>
| |
|
| |
| e) <math>8ax+24xy+64abxz</math>
| |
|
| |
| ====Frage 3====
| |
|
| |
| Gegeben sei die Steigung der Geraden <math>m = 3,5</math>. Außerdem verlaufe die Gerade durch den Punkt <math>P(2/5)</math>. Bestimme die Gleichung der Geraden in der Form <math>f(x) = mx + b</math>.
| |
|
| |
| <br />
| |
|
| |
| {{Box|Aufgabe 3: Wie lautet die Gleichung der Geraden?*|Gegeben sei die Steigung der Geraden <math>m = 3,5</math>. Außerdem verlaufe die Gerade durch den Punkt <math>P(2/5)</math>. Bestimme in deinem Heft die Gleichung der Geraden in der Form <math>f(x) = mx + b</math> und klicke dann auf das entsprechende Ergebnis.|Arbeitsmethode}}
| |
|
| |
| {{LearningApp|width:100%|height:500px|app=p0cp6e2a319}}
| |
|
| |
| {{Lösung versteckt|1=Setze die gegebenen Informationen in die Geradengleichung der Form <math>f(x) = mx + b</math> ein.|2=Tipp|3=Tipp}}
| |
|
| |
| {{Lösung versteckt|1 = Setze zunächst für die Steigung <math>m = 3,5</math>, sodass dein erstes Gerüst <math>f(x) = 3,5x + b</math> entsteht. Nutze in einem zweiten Schritt die Angabe des Punktes <math>P(2/5)</math>, sodass du mit <math>x = 2</math> und <math>f(x) = 5</math> die Gleichung <math>5 = 3,5*2 + b</math> erhältst. Bestimme nun mit Auflösung nach <math>b</math> den Wert <math>b = -2</math>, sodass sich schließlich die Geradengleichung <math>f(x) = 3,5x - 2</math> ergibt.|2 = Lösung|3 = Lösung}}
| |
|
| |
| {{Box|Aufgabe 4: Finde die gesuchte Geradengleichung!*|Bestimme in deinem Heft die Gleichung der Geraden, welche durch die Punkte <math>P(3/-4)</math> und <math>Q(8/6)</math> verläuft, in der Form <math>f(x) = mx + b</math> und klicke dann auf das entsprechende Ergebnis.|Arbeitsmethode}}
| |
|
| |
| {{LearningApp|width:100%|height:500px|app=pn2ojfrp319}}
| |
|
| |
| {{Lösung versteckt|1=Bestimme die Steigung der Geraden mithilfe der Punkte <math>P</math> und <math>Q</math>, indem du rechnest: <math>m = \frac{f(x)_Q - f(x)_P}{x_Q - x_P} = \frac{6 + 4}{8 - 3} = 2</math>. Wenn du Schwierigkeiten dabei hast, dir dieses Vorgehen zu erklären, stell dir vor, dass du an den Punkten <math>P</math> und <math>Q</math> des Graphen ein Steigungsdreieck zeichnest. Dann entspricht der Zähler der obigen Rechnung genau der Länge des y-Achsenabschnitts deines Steigungsdreiecks und der Nenner der obigen Rechnung der Länge des x-Achsenabschnitts deines Steigungsdreiecks.
| |
| Alternativ kannst du auch zwei Gleichungen erstellen, indem du die Angaben der Punkte <math>P(3/-4)</math>, d.h. <math>x = 3</math> und <math>f(x) = -3</math>, und <math>Q(8/6)</math>, d.h. <math>x = 8</math> und <math>f(x) = 6</math> nutzt.|2=Tipp 1|3=Tipp 1}}
| |
|
| |
| {{Lösung versteckt|1=Wenn du nach der ersten Variante vorgegangen bist, also die Steigung berechnet hast, dann wähle nun einen der beiden Punkte <math>P</math> oder <math>Q</math> und setze in <math>f(x) = 2x + b</math> die zugehörigen Werte für <math>x</math> und <math>f(x)</math> ein.
| |
| Wenn du nach der zweiten Variante vorgegangen bist, also zwei Gleichungen, jeweils mit den Unbekannten <math>m</math> und <math>b</math> aufgestellt hast, dann hast du ein lineares Gleichungssystem erhalten. Nun kannst du mithilfe des Eliminationsverfahrens zunächst die eine und dann die andere Unbekannte bestimmen.|2=Tipp 2|3=Tipp 2}}
| |
|
| |
| {{Lösung versteckt|1 = Wenn du nach der ersten Variante vorgehen möchtest, also erst die Steigung <math>m</math> und dann mithilfe eines der beiden Punkte <math>b</math> bestimmen möchtest, dann ergibt sich zunächst für die Steigung: <math>m = \frac{f(x)_Q - f(x)_P}{x_Q - x_P} = \frac{6 + 4}{8 - 3} = 2</math>. Im Anschluss erhältst du durch Einsetzen des Punktes <math>P</math> oder <math>Q</math> entweder <math>-4 = 2 * 3 + b</math> oder <math>6 = 2 * 8 + b</math>. Die Auflösung einer der beiden Gleichungen nach <math>b</math> liefert <math>b = -10</math>, sodass du schließlich die Funktionsgleichung <math>f(x) = 2x - 10</math> erhältst.
| |
| Wenn du nach der zweiten Variante vorgehen möchtest, stellst du mithilfe der beiden Punkte <math>P</math> und <math>Q</math> ein lineares Gleichungssystem zweier Gleichungen, jeweils mit den beiden Unbekannten <math>m</math> und <math>b</math> auf. Dann erhältst du die beiden Gleichungen <math>-4 = m * 3 + b</math> und <math>6 = m * 8 + b</math>. Ziehe nun die Gleichungen voneinander ab, sodass du <math>b</math> eliminieren kannst. Bestimme nun mithilfe der Auflösung nach <math>m</math> die Unbekannte <math>m = 2</math>. Setze nun ein eine der beiden Gleichungen dein Ergebnis für <math>m</math> ein und bestimme dann mithilfe der Auflösung nach <math>b</math> die Unbekannte <math>b = -10</math>. Damit erhältst du schließlich die Funktionsgleichung <math>f(x) = 2x - 10</math>.|2 = Lösung|3 = Lösung}}
| |