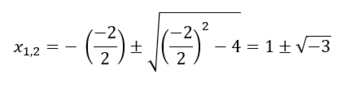|
|
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | Quelltext aus [[Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Terme und Gleichungen|Terme und Gleichungen]]: |
| | {{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> |
| | <span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> |
| | <span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> |
| | |
| | {{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} |
| | |
| | {{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel |
| | |
| | <math> x_{1,2} = - \frac{-2}{2} \pm \sqrt{\left( \frac{-2}{2} \right) ^2 -4}= 1 \pm \sqrt{-3}</math> |
| | |
| | , so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. <br /> '''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} |
| | |
| | |3=Arbeitsmethode }} |
| | |
| | Nicht verstandene Mathe-Formel durch Foto ersetzt: |
| | {{Box|1 = <span style="color: green"> Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br /> |
| | <span style="color: green"> a) </span> <math> x^2 - 2x + 4 = 0 </math> <br /> <br /> |
| | <span style="color: green"> b) </span> <math> \frac{x^2}{2} = x + \frac{3}{2} </math> <br /> <br /> |
| | |
| | {{Lösung versteckt|1= Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die <math> p </math> - <math> q </math> - Formel anwenden kannst. | 2= Tipp | 3= Tipp }} |
| | |
| | {{Lösung versteckt|1='''a)''' Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der <math> p </math> - <math> q </math> - Formel, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann. |
| | |
| | [[Datei:TG Lösung zu A7.3a.png|350px|Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)]] |
| | |
| | '''b)''' <math> x_1 = 3 ; x_2 = -1 </math> <br /> |2=Lösung|3=Lösung }} |
| | |
| | |3=Arbeitsmethode }} |
| | |
| | |
| ===Spielwiese=== | | ===Spielwiese=== |
|
| |
|
| Zeile 110: |
Zeile 141: |
| |2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | | |2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} |
| |Arbeitsmethode}} | | |Arbeitsmethode}} |
|
| |
|
| |
|
| |
|
| |
| <span style="color: blue">'''b)''' Gegeben sind die beiden Geraden <math>f(x)=4x-5</math> und <math>g(x)=-3x+9</math>.</span>
| |
| {{Lösung versteckt|1 = Der Schnittpunkt liegt bei x= 2 und y = 3. Wie komme ich zu meiner Lösung? Ich setze die beiden Funktionen <math>g(x)</math> und <math>h(x)</math> gleich. Dann erhalte ich <math>4x-5=-3x+9</math>.Dann löse ich nach x auf. Ich erhalte den Wert x = 2. Jetzt kann ich den Wert x=2 in eine der beiden Gleichungen einsetzen und den y-Wert berechnen |2=Lösung|3=Lösung}}
| |
|
| |
|
| |
| <span style="color: green">'''c)''' Gegeben sind die beiden Geraden <math>f(x)= \frac{3}{2}x-3</math> und <math>g(x)= \frac{1}{2}x+17</math>.</span>
| |
| {{Lösung versteckt|1 = Der Schnittpunkt liegt bei x= 20 und y = 27. Wie komme ich zu meiner Lösung? Ich setze die beiden Funktionen <math>f(x)</math> und <math>h(x)</math> gleich. Dann erhalte ich <math>\frac{3}{2}x-3=\frac{1}{2}x+17</math>. Nun löse ich nach x auf. Ich erhalte den Wert x = 20. Jetzt kann ich den Wert x=20 in eine der beiden Gleichungen einsetzen und den y-Wert berechnen. |2=Lösung|3=Lösung}}
| |
Quelltext aus Terme und Gleichungen:
Aufgabe 7.3
Löse folgende quadratische Gleichungen.
a) 
b) 
Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die

-

- Formel anwenden kannst.
a) Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der  -
-  - Formel
- Formel

, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann.
b) 
Nicht verstandene Mathe-Formel durch Foto ersetzt:
Aufgabe 7.3
Löse folgende quadratische Gleichungen.
a) 
b) 
Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die

-

- Formel anwenden kannst.
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Ganz einfach per Mausklick aktivierbar
Dateien
Bild aus ZUM Projekte:
Bild aus Wikipedia:
Interaktive Applets
LearningApp:
Geogebra-Applet:
Kombinationen
Quadratische Funktionen in Scheitelpunktform
(Inhalte aus dem Lernpfad Quadratische Funktionen erkunden)
Merke
Terme quadratischer Funktionen können in der Form  angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten
angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten  .
.
Der Parameter "

"
Was passiert, wenn man statt der Funktion  folgende Funktionen gegeben hat:
folgende Funktionen gegeben hat:
- (1)
 , (2)
, (2)  und (3)
und (3)  ?
?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!).
Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die drei Funktionen aufstellen und die Funktionswerte mit den Werten von

vergleichen.
b) Überprüfe deine Vermutungen aus Aufgabenteil a) mit dem folgenden Geogebra-Applet. Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?
In dem Applet ist die Normalparabel  grau eingezeichnet. Du kannst verschiedene Werte für "
grau eingezeichnet. Du kannst verschiedene Werte für " " eingeben. Dadurch wird der grüne Graph
" eingeben. Dadurch wird der grüne Graph  verändert.
verändert.
Aufgabe 2
a) Beantworte die Fragen bitte selbstständig. Es ist jeweils genau eine Antwort richtig.
Aufgabe 3
Finde Werte für a, d und e, so dass  die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.
die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. Wenn du noch weiter arbeiten möchtest, kannst du auch einige der übrigen Hintergundbilder bearbeiten.